Đề thi thử tốt nghiệp THPT 2025 môn Toán lần 3 trường THPT Bá Thước, Thanh Hóa
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
1/4 - Mã đề 470
SỞ GD&ĐT THANH HÓA
TRƯỜNG THPT BÁ THƯỚC
(Đề thi có 04 trang)
ĐỀ THI THỬ TỐT NGHIỆP LẦN 3
NĂM HỌC 2024 - 2025
Môn: Toán
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ...................
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Tập nghiệm của bất phương trình
2
4
11
2 32
xx+
>
là
A.
{
}
5;1−
. B.
( ; 5) (1; )−∞ − ∪ +∞
. C.
( 5;1)−
. D.
(1; )+∞
.
Câu 2. Phương trình
2
1
3
9
x−
=
có nghiệm
A.
19
.
9
x =
B.
4x =
. C.
0.x =
D.
2.x =
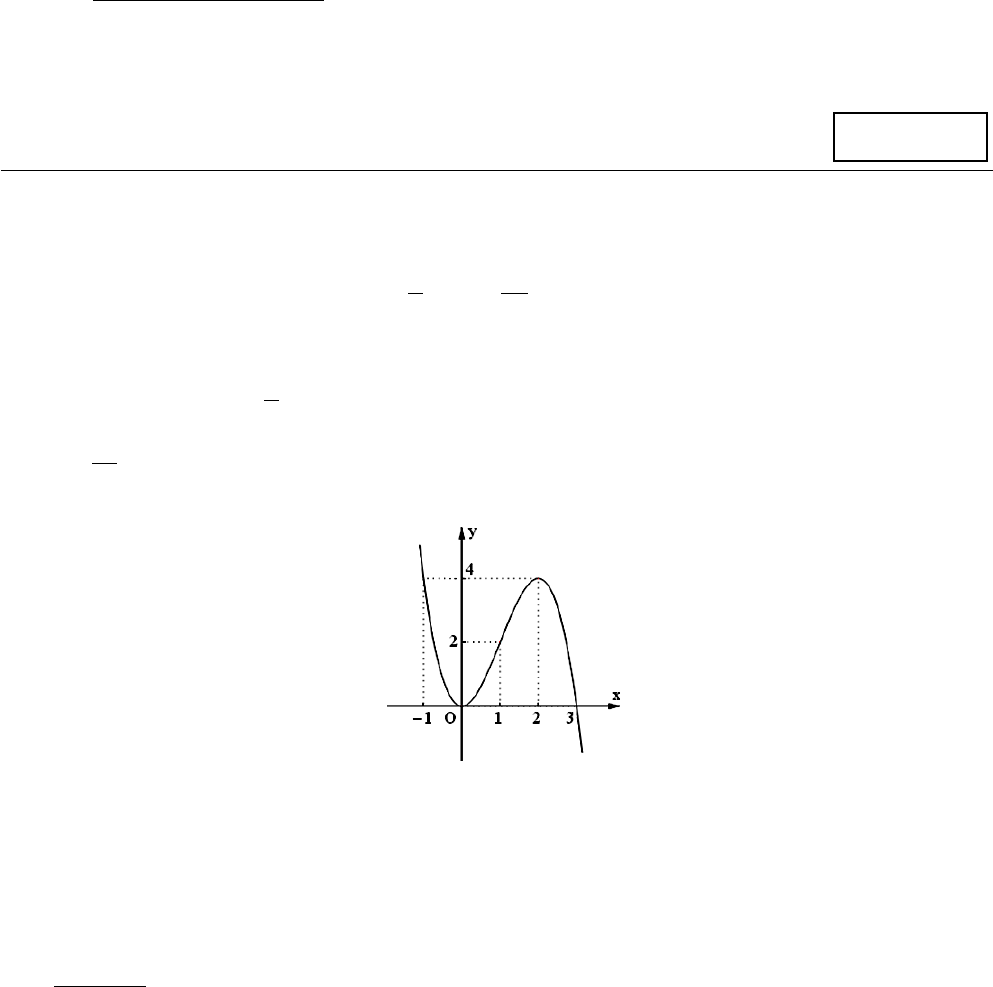
Câu 3. Cho hàm số có đồ thị như hình vẽ bên. Phát biểu nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
( )
2;+∞
.
B. Điểm cực tiểu của đồ thì hàm số là
( )
0;0
.
C. Hàm số đồng biến trên khoảng
( )
0;2
.
D. Điểm cực đại của hàm số là
4
.
Câu 4. Nguyên hàm của hàm số
( )
2025
x
fx=
A.
( )
2025
ln 2025
x
C+
. B.
2025
x
C+
. C.
2025.2024
x
C+
. D.
2025xC
+
.
Câu 5. Cho hình hộp
.''' 'ABCD A B C D
(minh họa như hình bên). Phát biểu nào sau đây là sai?
A.
''BB BA BC BD++ =
. B.
''AA AC AC+=
.
C.
''AB AD A C+=
. D.
''DA DC B D+=
Câu 6. Cho cấp số cộng
( )
n
u
có
23
2, 1uu=−=
. Số hạng
4
u
của cấp số cộng là:
A.
6
B.
5
C.
4
D.
7
Câu 7. Cho hình chóp tứ giác đều
.S ABCD
. Gọi
H
là trung điểm của cạnh
AC
. Tìm mệnh đề sai?
A.
( ) ( )
SAC SBD⊥
. B.
( )
CD SAD
⊥
. C.
( )
SH ABCD
⊥
. D.
( ) ( )
SBD ABCD⊥
.
Câu 8. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 3 2 50Px y z− + −=
và hai điểm
( )
2;4;1A
,
( )
1;1; 3B −
. Mặt phẳng
( )
Q
đi qua hai điểm
,AB
và vuông góc với mặt phẳng
( )
P
. Một vectơ pháp
tuyến của mặt phẳng
( )
Q
là
A.
( )
2
3; 3; 2n =−−
. B.
( )
3
0;8;12n =
. C.
( )
4
1; 3; 2n =
. D.
( )
1
1; 3; 2n = −
.
Mã đề 470
2/4 - Mã đề 470
Câu 9. Tiệm cận xiên của đồ thị hàm số
2
25
2
xx
y
x
−− +
=
+
là
A.
.yx= −
B.
2.yx= +
C.
2.
x
= −
D.
1.yx=−+
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, phương trình mặt cầu
( )
S
tâm
( )
2; 1; 0I −
và có đường
kính bằng 8 là
A.
( ) ( ) ( )
22
2
: 2 1 16Sx y z− ++ +=
. B.
( ) ( ) ( )
22
2
: 2 1 64Sx y z+ +−+=
.
C.
( ) ( ) ( )
22
2
: 2 1 64Sx y z− ++ +=
. D.
( ) ( ) ( )
22
2
:2 1 8Sx y z+ +−+=
.
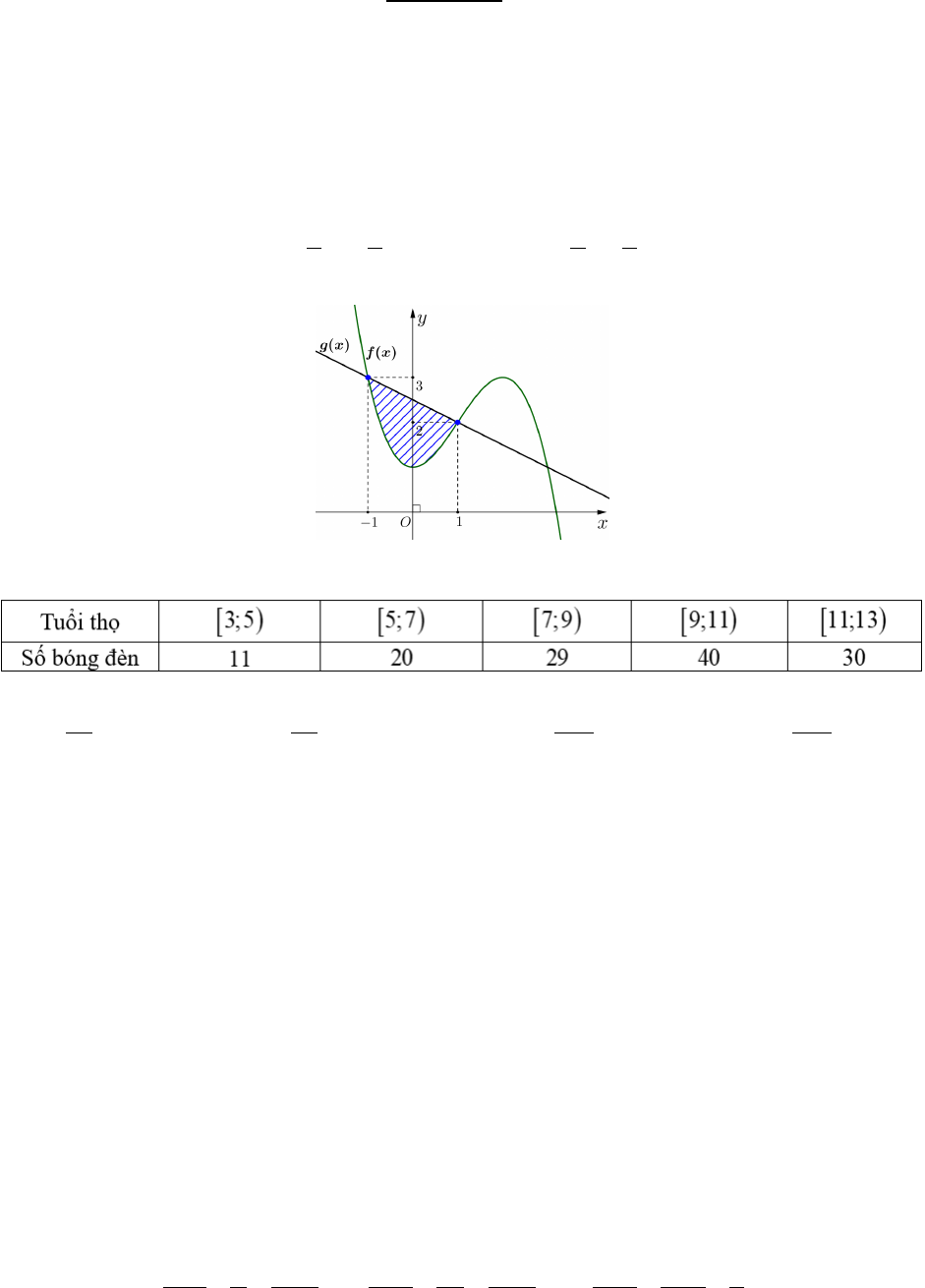
Câu 11. Cho hai hàm số
( )
32
13
1
22
fx x x=−++
và
( )
15
22
gx x=−+
có đồ thị như hình vẽ bên dưới.
Diện tích phần gạch chéo trong hình bằng
A. 4. B. 2. C. 8. D. 1.
Câu 12. Cho bảng số liệu khảo sát về tuổi thọ (đơn vị: nghìn giờ) của một loại bóng đèn:
Giá trị của tứ phân vị thứ nhất là
A.
1
37
4
Q =
. B.
1
87
8
Q =
. C.
1
875
232
Q =
. D.
1
206
29
Q =
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13. Trong cuộc thi tìm kiếm năng khiếu âm nhạc do đoàn trường THPT Bá Thước tổ chức, ban tổ
chức tổ chức ba vòng thi: vòng sơ khảo, vòng bán kết và vòng chung kết. Biết rằng, ban tổ chức sẽ chọn
ra
50%
đội thi đã đăng kí để vào vòng sơ khảo. Khi kết thúc vòng sơ khảo, ban tổ chức sẽ chọn ra
30%
đội thi của vòng sơ khảo để vào vòng bán kết. Khi kết thúc vòng bán kết, ban tổ chức sẽ chọn ra
20%
đội
thi của vòng bán kết để vào vòng chung kết. Chọn ngẫu nhiên một đội thi đã đăng kí tham dự cuộc thi
này.
A. Xác suất để đội thi được chọn lọt vào vòng sơ khảo là
0,5
.
B. Xác suất để đội thi được chọn lọt vào vòng bán kết là
0,3
.
C. Biết rằng đội thi được chọn không lọt vào vòng chung kết. Khi đó, xác suất đội thi ấy lọt vào vòng sơ
khảo nhỏ hơn
0, 4
.
D. Xác suất để đội thi được chọn lọt vào vòng chung kết là
0,03
.
Câu 14. Trong không gian Oxyz, cho điểm
( )
1;2;2A
,
( )
3; 0; 2B −
, mặt phẳng
( )
: 40Pxyz−+−=
và
các đường thẳng
12
1 21 2
: ,:
21 1 1 22
x yz x y z− +− +
∆==∆==
−−
,
3
11
:
1 21
xyz+−
∆==
và
4
23
:2
3
xt
yt
z
=−+
∆=−
= −
.
A. Phương trình mặt cầu đường kính
AB
là
( ) ( ) ( )
22 2
1 1 25xyz− ++ ++ =
.
B. Đường thẳng
∆
cắt cả 4 đường thẳng
1234
,,,∆∆∆∆
có một véc tơ chỉ phương là
( )
3;2;2u
∆
=
.
3/4 - Mã đề 470
C. Nếu mặt phẳng
( )
α
đi qua A cắt các trục
,,Ox Oy Oz
lần lượt tại
,,MNP
sao cho tam giác
MNP
có
trọng tâm là A thì phương trình của
( )
α
là
2 60xyz++−=
.
D. Gọi D là điểm thay đổi trên mặt phẳng (P) và E là điểm thay đổi trên mặt phẳng (Oxy). Chu vi tam
giác ADE có giá trị nhỏ nhất bằng
2 11
.
Câu 15. Đồ thị của hàm số
y ax b
x
c
d
= ++
+
là hình dưới đây
A.
1
lim
x
y
+
→
= −∞
.
B. Phương trình đường tiệm cận xiên của đồ thị hàm số là
1
yx= +
.
C. Tổng
2abcd+++ =
.
D. Hàm số nghịch biến trên khoảng
( )
0;1
.
Câu 16. Cho hàm số
( )
1
sin
2
fx x x=−−
A. Giá trị nhỏ nhất của hàm số
(
)
fx
trên
[0; ]
π
là
2
π
−
.
B.
( )
2f
ππ
=
.
C.
( )
1
cos
2
fx x
′
=−−
.
D. Phương trình
( )
0fx
′
=
có 2 nghiệm phân biệt trong khoảng
[0; ]
π
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
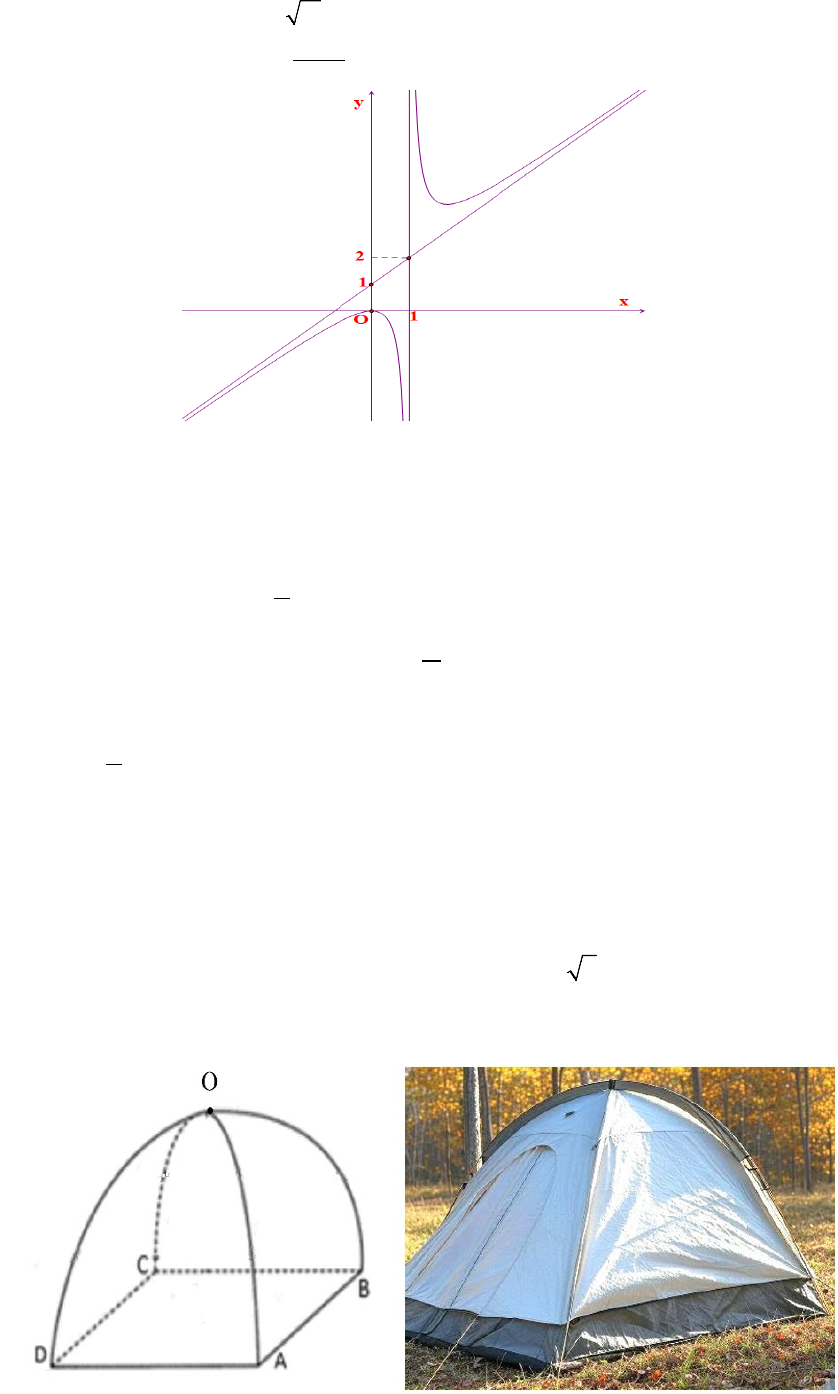
Câu 17. Một lều cắm trại có dạng như hình vẽ dưới, khung lều được tạo thành từ hai parabol giống nhau
có chung đỉnh O và thuộc hai mặt phẳng vuông góc nhau (một parabol đi qua
,,AOC
và một parabol đi
qua
,,BDO
), bốn chân tạo thành hình vuông
ABCD
có cạnh là
( )
22m
, chiều cao tính từ đỉnh lều là
( )
2 m
. Biết mặt cắt của lều khi cắt bởi một mặt phẳng song song với mặt phẳng
(
)
ABCD
luôn là một
hình vuông. Tính thể tích của lều (đơn vị là
3
m
)
Đề thi thử tốt nghiệp môn Toán trường Bá Thước, Thanh Hóa
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán lần 3 trường THPT Bá Thước, Thanh Hóa có đáp án được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Bài viết được tổng hợp gồm có 2 mã đề thi. Đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi đề thi dưới đây để có thêm tài liệu ôn thi kì Thi THPT Quốc gia sắp tới nhé.


