Tìm m để hàm số đồng biến, nghịch biến trên khoảng
Tìm m để hàm số đồng biến, nghịch biến trên khoảng
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
I. Phương pháp giải bài toán tìm m để hàm số đồng biến, nghịch biến trên khoảng
- Định lí: Cho hàm số 
\(y=f\left( x \right)\) có đạo hàm trên khoảng \(\left( a,b \right)\):
+ Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( a,b \right)\) khi và chỉ khi \(f'\left( x \right)\ge 0\) với mọi giá trị x thuộc khoảng \(\left( a,b \right)\). Dấu bằng xảy ra tại hữu hạn điểm.
+ Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng \(\left( a,b \right)\) khi và chỉ khi \(f'\left( x \right)\le 0\) với mọi giá trị x thuộc khoảng \(\left( a,b \right)\). Dấu bằng xảy ra tại hữu hạn điểm.
1. Tìm m để hàm số đồng biến, nghịch biến trên từng khoảng xác định
Chương trình phổ thông ta thường gặp dạng bài này đối với hàm số đa thức bậc 1 trên bậc 1, ta sẽ áp dụng chú ý sau:
- Hàm số \(f\left( x \right)=\frac{ax+b}{cx+d},\left( ad-bc\ne 0,c\ne 0 \right)\) đồng biến trên từng khoảng xác định khi và chỉ khi \(ad-bc>0\)
- Hàm số \(f\left( x \right)=\frac{ax+b}{cx+d},\left( ad-bc\ne 0,c\ne 0 \right)\) nghịch biến trên từng khoảng xác định khi và chỉ khi \(ad-bc<0\)
2. Tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước.
Cách 1:
|
- Hàm số
- Hàm số |
Cách 2: Cô lập tham số m
Bước 1: Tìm y’
Bước 2: Cô lập m ta sẽ thu được phương trình ví dụ \(m\ge f\left( x \right)\)
Bước 3: Xét dấu với hàm \(f\left( x \right)\) theo bảng quy tắc sau:
|
|
II. Ví dụ minh họa tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước.
Ví dụ 1: Tìm m để hàm số \(y=-{{x}^{3}}+3{{x}^{2}}+3mx-1\) nghịch biến trên khoảng \(\left( 0,+\infty \right)\)
| \(A. m\ge 1\) |
\(B. m\le -1\) |
| \(C.m\ge -1\) |
\(D. m\le 0\) |
Hướng dẫn giải
Ta có: \(y'=-3{{x}^{2}}+6x+3m\)
Hàm số nghịch biến trên \(\left( 0,+\infty \right)\Leftrightarrow y'\le 0\) với mọi \(x\in \left( 0,+\infty \right)\)
\(\Leftrightarrow -3{{x}^{2}}+6x+3m\le 0,\forall x\in \left( 0,+\infty \right)\Leftrightarrow m\le {{x}^{2}}-2x,\forall x\in \left( 0,+\infty \right)\)
Xét \(f\left( x \right)={{x}^{2}}-2x\) với \(x\in \left( 0,+\infty \right)
f'\left( x \right)=2x-2,f'\left( x \right)=0\Leftrightarrow x=1\)
Học sinh tự vẽ bảng biến thiên và áp dụng quy tắc ta nhận được kết quả \(m\le -1\)
Đáp án B
Ví dụ 2: Tìm tất cả giá trị của m để hàm số \(y=-\frac{1}{3}{{x}^{3}}+\left( m-1 \right){{x}^{2}}+\left( m+3 \right)x-1\) đồng biến trên khoảng \(\left( 0,3 \right)\).
| \(A. m\le -3\) |
\(B. m\ge \frac{1}{5}\) |
| \(C.m\ge \frac{11}{3}\) |
\(D. m\ge \frac{12}{7}\) |
Hướng dẫn giải
Ta có: \(y'=-{{x}^{2}}+2\left( m-1 \right)x+3+m\)
Hàm số đồng biến trên \(\left( 0,3 \right)\Rightarrow y'\ge 0,\forall x\in \left( 0,3 \right)\)
\(\Rightarrow -{{x}^{2}}+2\left( m-1 \right)x+3+m\ge 0\Leftrightarrow m\ge \frac{{{x}^{2}}+2x+3}{2x+1}\)
Xét hàm số: \(f\left( x \right)=\frac{{{x}^{2}}+2x+3}{2x+1}\) với \(\forall x\in \left( 0,3 \right)
\Rightarrow f\left( x \right)=\frac{{{x}^{2}}+2x+3}{2x+1},\forall x\in \left( 0,3 \right)\)
Lập bảng biến thiên kết luận \(m\ge \frac{12}{7}\)
Đáp án D
Ví dụ 3: Tìm m để hàm số \(y=\frac{\tan x-2}{\tan x-m}\) đồng biến trên \(\left( 0,\frac{\pi }{4} \right)\)
| \(A. m\ge 2\) |
\(B. m\le 0\) |
| \(C.1\le m<2\) |
\(D. \left[ \begin{matrix}
m\le 0 \\
1\le m<2 \\
\end{matrix} \right.\) |
Hướng dẫn giải
\(y'=\frac{-m+2}{{{\left( \tan x-m \right)}^{2}}}\left( \tan x \right)'=\frac{-m+2}{{{\left( \tan x-m \right)}^{2}}}.\frac{1}{{{\cos }^{2}}x}\)
Để hàm số đồng biến trên \(\left( 0,\frac{\pi }{4} \right)\) thì:
\(y'>0,\forall x\in \left( 0,\frac{\pi }{4} \right)\Leftrightarrow \left\{ \begin{matrix}
-m+2>0 \\
m\ne \tan x,x\in \left( 0,\dfrac{\pi }{4} \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
m<2 \\
m\notin \left( 0,1 \right) \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
m\le 0 \\
1\le m<2 \\
\end{matrix} \right.\)
Đáp án D
Ví dụ 4. Hàm số \(y = \frac{1}{3}x^{3} +
\frac{m}{2}x^{2} + x + 6\) đồng biến trên nửa khoảng \(\lbrack 1; + \infty)\) khi nào?
Hướng dẫn giải
Ta có: \(y' = x^{2} + mx +
1\)
Để hàm số đã cho đồng biến trên nửa khoảng \(\lbrack 1; + \infty)\) khi đó:
\(\Leftrightarrow y' \geq 0;\forall x
\in \lbrack 1; + \infty)\)
\(\Leftrightarrow x^{2} + mx + 1 \geq
0;\forall x \in \lbrack 1; + \infty)\)
\(\Leftrightarrow m \geq - x -
\frac{1}{x};\forall x \in \lbrack 1; + \infty)\)
Xét hàm số \(g(x) = - x -
\frac{1}{x}\) trên nửa khoảng \(\lbrack
1; + \infty)\) ta có:
\(g'(x) = - 1 + \frac{1}{x^{2}} =
\frac{1 - x^{2}}{x^{2}}\)
\(g'(x) = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 1 \\
x = - 1 \\
\end{matrix} \right.\)
Bảng biến thiên của hàm số \(g(x) = - x -
\frac{1}{x}\) trên nửa khoảng \(\lbrack
1; + \infty)\) là:
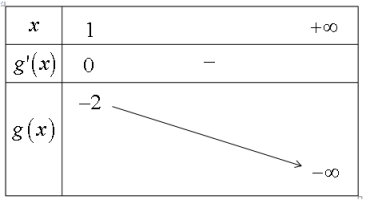
Từ bảng biến thiên suy ra \(\max_{\lbrack
1; + \infty)}g(x) = g(1) = - 2\)
Vậy \(m \geq g(x);\forall x \in \lbrack 1;
+ \infty)\) khi và chỉ khi \(m \geq -
2\).
Ví dụ 5 . Xác định điều kiện của tham số m để hàm số \(y = f(x) = - x^{3} + 3x^{2} + (2m - 1)x -
1\) nghịch biến trên khoảng \((0; +
\infty)\) ?
Hướng dẫn giải
Tập xác định \(D\mathbb{= R}\)
Ta có:\(y' = - 3x^{2} + 6x + 2m -
1\)
Hàm số đã cho nghịch biến trên khoảng \((0;
+ \infty)\)
\(y' \leq 0;\forall x \in (0; +
\infty)\) khi và chỉ khi
\(\Leftrightarrow 2m \leq 3x^{2} - 6x +
1;\forall x \in (0; + \infty)\)
Xét hàm số \(g() = 3x^{2} - 6x + 1\) trên \((0; + \infty)\) ta có bảng biến thiên như sau:
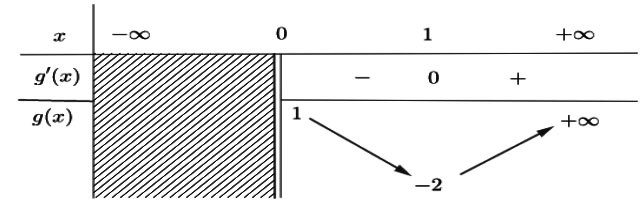
Dựa vào bảng biến thiên ta có:
\(\min_{(0; + \infty)}g(x) = -
2\)
Do đó \(\Leftrightarrow 2m \leq \min_{(0; +
\infty)}g(x) \Leftrightarrow 2m \leq - 2 \Leftrightarrow m \leq -
1\)
Vậy \(m \leq - 1\) thỏa mãn yêu cầu bài toán.
Ví dụ 6. Cho hàm số \(y = \frac{m^{2}x +
5}{2mx + 1}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các số nguyên \(m \in \lbrack - 2020;2020\rbrack\) để hàm số đã cho nghịch biến trên khoảng \((3; +
\infty)\). Xác định số phần tử của tập hợp \(S\)?
Hướng dẫn giải
Xét \(m = 0 \Rightarrow y = 5\) là hàm hằng nên hàm số không nghịch biến. Vậy \(m
= 0\) không thỏa mãn.
Xét \(m \neq 0\)
Tập xác định \(D = \left( - \infty; -
\frac{1}{2m} \right) \cup \left( - \frac{1}{2m}; + \infty
\right)\)
Để hàm số nghịch biến trên khoảng \((3; +
\infty)\) khi và chỉ khi
\(\left\{ \begin{matrix}
y' = \frac{m^{2} - 10m}{(2mx + 1)^{2}} < 0 \\
- \frac{1}{2m} \leq 3 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m^{2} - 10m < 0 \\
\frac{6m + 1}{2m} \geq 0 \\
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
0 < m < 10 \\
\left\lbrack \begin{matrix}
m \leq - \frac{1}{6} \\
m > 0 \\
\end{matrix} \right.\ \\
\end{matrix} \right.\ \Leftrightarrow 0 < m < 10\)
Mà \(\left\{ \begin{matrix}
m\mathbb{\in Z} \\
m \in \lbrack - 2020;2020\rbrack \\
\end{matrix} \right.\) nên \(m \in
\left\{ 1;2;3;...;9 \right\}\)
Vậy tập hợp S có tất cả 9 giá trị.
Ví dụ. Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y
= \frac{1}{3}(m + 2)x^{3} - (m + 2)x^{2} + (m - 8)x + m^{2} - 1\) luôn nghịch biến trên \(\mathbb{R}\)?
Hướng dẫn giải
Với \(m = - 2\) ta có \(y = - 10x + 3\) (hàm số này luôn nghịch biến trên tập số thực)
Với \(m \neq - 2\) ta có \(y' = (m + 2)x^{2} - 2(m + 2)x + m -
8\)
Hàm số nghịch biến trên\(\mathbb{R
\Leftrightarrow}y' \leq 0\left( \forall x\mathbb{\in R}
\right)\)
\(\Leftrightarrow \left\{ \begin{matrix}
a_{y'} = m + 2 < 0 \\
\Delta'_{y'} = \leq 0 \\
\end{matrix} \right.\ \Leftrightarrow - 2 \leq m \leq - 2\)
Kết hợp với \(m\mathbb{\in Z \Rightarrow}m
\in \left\{ - 2; - 1;0;1;2 \right\}\)
Vậy số phần tử của tập hợp \(S\) là 5.
II. Bài tập tự luyện
Câu 1: Tìm tất cả các giá trị thực của tham số m sao cho hàm số: \(y=\frac{m-\sin x}{{{\cos }^{2}}x}\) nghịch biến trên khoảng \(\left( 0,\frac{\pi }{6} \right)\)
| \(A. m\ge \frac{5}{4}\) |
\(B. m\le \frac{5}{4}\) |
| \(C. m\ge \frac{5}{2}\) |
\(D. m\le \frac{5}{2}\) |
Câu 2: Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=\frac{\left( m+1 \right)x+2m+2}{x+m}\) nghịch biến trên khoảng \(\left( -1,+\infty \right)\)
| \(A. -1< m <2\) |
\(B. m\ge 1\) |
| \(C. 1\le m<2\) |
\(D. \left[ \begin{matrix}
m>2 \\
m<1 \\
\end{matrix} \right.\) |
Câu 3: Với giá trị nào của m thì hàm số \(y=\frac{mx+4}{x+m}\) nghịch biến trên \(\left( -\infty ,1 \right)\)
| \(A. -2\le m\le 1\) |
\(B. -2\le m\le -1\) |
| \(C. m\in \varnothing\) |
\(D. -2 < m <2\) |
Câu 4: Tìm m để hàm số \(y=\frac{2{{x}^{2}}-3x+m}{x-1}\) đồng biến trên \(\left( 2,+\infty \right)\)
| \(A. m\ge -1\) |
\(B. m\ge 2\) |
| \(C.m\le 3\) |
\(D. m\le 7\) |
Câu 5: Tìm m để hàm số \(y=\sin x+mx\) đồng biến trên \(\mathbb{R}\)
| \(A. m\ge -1\) |
\(B. m\ge 2\) |
| \(C.m\ge 1\) |
\(D. m\le 7\) |
Câu 6: Tìm m để hàm số \(y=\frac{\sin x-1}{\sin x+m}\) nghịch biến trên \(\left( 0,\frac{\pi }{2} \right)\)
| \(A. m\ge 0\) |
\(B. m\le 0\) |
| \(C.m\ge -1\) |
\(D. m\le 1\) |
Câu 7: Tìm tất cả các giá trị của m để hàm số \(y=\frac{{{e}^{x}}-m-2}{{{e}^{x}}-{{m}^{2}}}\) nghịch biến trên khoảng \(\left( \ln \frac{1}{4},0 \right)\)
| \(A. 1< m <2\) |
\(B. -1\le m\le 2\) |
| \(C. -\frac{1}{2}\le m\le \frac{1}{2}\) |
\(D. \left[ \begin{matrix}
-\dfrac{1}{2}\le m\le \dfrac{1}{2} \\
1\le m<2 \\
\end{matrix} \right.\) |
Câu 8: Cho hàm số \(y = \frac{{\left( {m - 1} \right)\sqrt {x - 1} + 2}}{{\sqrt {x - 1} - 1}}\). Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (17;37).
| A. m ∈ [-4; -1] | B. m ∈ (-∞; -6] ∪ [-4; -1) ∪ (2; +∞) |
| C. m ∈ (-∞; -4] ∪ (2; +∞) | D. m ∈ (-1; 2) |
Câu 9: Hàm số: y = 2x3 - 3(2m + 1)x2 + 6m(m + 1)x + 1 đồng biến trên khoảng (2;+∞) khi giá trị m là?
| A. m ≤ 2 | B. m ≥ 2 |
| C. m ≤ 1 | D. m ≥ 1 |
Câu 10: Cho hàm số: \(y=\frac{{{x^2} - 2mx + 3{m^2}}}{{x - 2m}}\) đồng biến trên từng khoảng xác định của nó khi giá trị của tham số m là:
| A. m < 0 | B. m > 0 |
| C. m = 0 | D. m ∈ R |
Câu 11: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2017 ] để hàm số y = (m - 2)x + 2m đồng biến trên R.
| A. 2014 | B. 2016 |
| C. vô số | D. 2015 |
Câu 12: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2017 ] để hàm số y =(m2-4)x + 2m đồng biến trên R.
| A. 4030 | B. 4034 |
| C. Vô số | D. 2015 |
Câu 13: Tìm tất cả các giá trị thực của tham số số m để hàm số \(y = \frac{{\cot x - 1}}{{m\cot x - 1}}\) đồng biến trên khoảng \(\left( {\frac{\pi }{4};\frac{\pi }{2}} \right)\)
| A. m ∈ (-∞ ; 0) ∪ (1 ;+∞) | B. m ∈ (-∞ ; 0) |
| C. m ∈ (1 ; +∞) | D. m ∈ (-∞ ; 1) |
Câu 14: Tìm tất cả các giá trị của tham số m để hàm số y = ln (16x2 + 1) - (m +1)x + m + 2 nghịch biến trên khoảng ( -∞; +∞)
| A. m ∈ (-∞ ; -3] | B. m ∈ [3 ; +∞ ) |
| C. m ∈ (-∞ ; -3) | D. m ∈ [-3 ; 3] |
Câu 15: Cho hàm số y = x3 + 3x2. Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số đồng biến trên (-∞ ; -2) và (0 ;+∞)
B. Hàm số nghịch biến trên (-2 ; 1)
C. Hàm số đồng biến trên khoảng (-∞ ; 0) và (2 ;+∞)
D. Hàm số nghịch biến trên khoảng (-∞ ; -2) và (0 ;+∞)
Kiểm tra kiến thức về đồng biến, nghịch biến:
Bài trắc nghiệm được biên soạn bởi KhoaHoc.vn - Chuyên trang học online!
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Tìm m để hàm số đồng biến, nghịch biến trên khoảng. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.
- Tìm m để hàm số đồng biến, nghịch biến trên R
- 300 câu hỏi trắc nghiệm môn Toán lớp 12 (Có đáp án)
- Bài tập trắc nghiệm cực trị của hàm số và điểm uốn (Có đáp án)
- Bài tập trắc nghiệm tính đơn điệu của hàm số
- Câu hỏi trắc nghiệm môn Toán lớp 12: Cực trị của hàm số
Lịch thi THPT Quốc Gia 2025
Xem chi tiết lịch thi: Lịch thi tốt nghiệp THPT Quốc Gia 2025
Gửi đề thi để nhận lời giải ngay: https://www.facebook. com/com.VnDoc
