Tổng hợp công thức phương trình mặt phẳng trong không gian
Công thức phương trình mặt phẳng
Bạn đang ôn tập hình học không gian và cần tổng hợp đầy đủ công thức phương trình mặt phẳng? Tài liệu dưới đây sẽ giúp bạn hệ thống hóa các công thức quan trọng liên quan đến mặt phẳng trong không gian Oxyz, bao gồm: phương trình tổng quát, phương trình mặt phẳng qua 3 điểm, mặt phẳng song song, vuông góc, v.v. Các công thức được trình bày ngắn gọn, dễ nhớ, kèm theo ví dụ minh họa giúp bạn áp dụng hiệu quả trong bài tập và các kỳ thi.
A. Vectơ pháp tuyến của mặt phẳng
Vectơ 
\(\overrightarrow{n} \neq
\overrightarrow{0}\) là vectơ pháp tuyến (VTPT) nếu giá của \(\overrightarrow{n}\) vuông góc với mặt phẳng \((\alpha)\).
Chú ý:
- Nếu \(\overrightarrow{n}\) là một VTPT của mặt phẳng \((\alpha)\) thì \(k\overrightarrow{n}\ \ (k \neq 0)\) cũng là một VTPT của mặt phẳng\((\alpha)\).
- Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.
- Nếu \(\overrightarrow{u},\
\overrightarrow{v}\) có giá song song hoặc nằm trên mặt phẳng \((\alpha)\) thì \(\overrightarrow{n} = \lbrack\overrightarrow{u},\
\overrightarrow{v}\rbrack\) là một VTPT của \((\alpha)\).
B. Phương trình tổng quát của mặt phẳng
Trong không gian \(Oxyz\), mọi mặt phẳng đều có dạng phương trình:
\(Ax + By + Cz + D = 0\\)với \(A^{2} + B^{2} + C^{2} \neq 0\)
- Nếu mặt phẳng \((\alpha)\) có phương trình \(Ax + By + Cz + D = 0\\)thì nó có một VTPT là \(\overrightarrow{n}(A;\ B;\
C)\).
- Phương trình mặt phẳng đi qua điểm \(M_{0}(x_{0};y_{0};z_{0})\) và nhận vectơ \(\overrightarrow{n}(A;\ B;\ C)\) khác \(\overrightarrow{0}\) là VTPT là:
\(A(x - x_{0}) + B(y - y_{0}) + C(z -
z_{0}) = 0\)
Các trường hợp riêng
Xét phương trình mặt phẳng \((\alpha)\): \(Ax
+ By + Cz + D = 0\\)với \(A^{2} +
B^{2} + C^{2} \neq 0\)
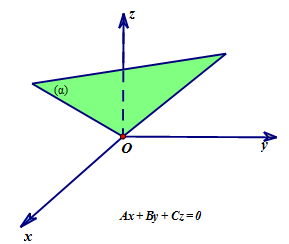
Nếu \(D = 0\) thì mặt phẳng \((\alpha)\) đi qua gốc tọa độ \(O\).
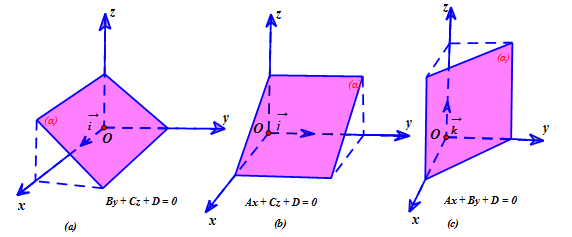
- Nếu \(A = 0,B \neq 0,C \neq 0\) thì mặt phẳng \((\alpha)\) song song hoặc chứa trục \(Ox\).
- Nếu \(A \neq 0,B = 0,C \neq 0\) thì mặt phẳng \((\alpha)\) song song hoặc chứa trục \(Oy\).
- Nếu \(A \neq 0,B \neq 0,C = 0\) thì mặt phẳng \((\alpha)\) song song hoặc chứa trục \(Oz\).
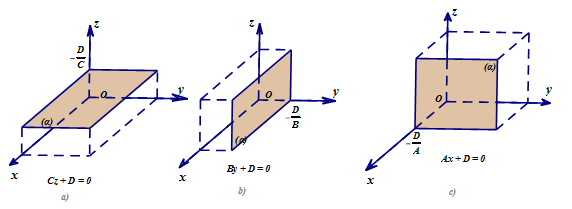
- Nếu \(A = B = 0,C \neq 0\) thì mặt phẳng \((\alpha)\) song song hoặc trùng với \((Oxy)\).
- Nếu \(A = C = 0,B \neq 0\) thì mặt phẳng \((\alpha)\) song song hoặc trùng với \((Oxz)\).
- Nếu \(B = C = 0,A \neq 0\) thì mặt phẳng \((\alpha)\) song song hoặc trùng với \((Oyz)\).
Chú ý:
- Nếu trong phương trình \((\alpha)\) không chứa ẩn nào thì \((\alpha)\) song song hoặc chứa trục tương ứng.
- Phương trình mặt phẳng theo đoạn chắn \((\alpha):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} =
1\). Ở đây \((\alpha)\) cắt các trục tọa độ tại các điểm \((a;0;0)\), \((0;b;0)\), \((0;0;c)\) với \(abc \neq 0\).
C. Khoảng cách từ một điểm đến một mặt phẳng.
Trong không gian \(Oxyz\), cho điểm \(M_{0}(x_{0};y_{0};z_{0})\) và mặt phẳng \((\alpha):Ax + By + Cz + D =
0\)
Khi đó khoảng cách từ điểm \(M_{0}\) đến mặt phẳng \((\alpha)\) được tính:
\(d(M_{0},(\alpha)) = \frac{|Ax_{0} +
By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}\)
D. Góc giữa hai mặt phẳng
Trong không gian \(Oxyz\), cho hai mặt phẳng \((\alpha):A_{1}x + B_{1}y + C_{1}z
+ D_{1} = 0\) và \((\beta):A_{2}x +
B_{2}y + C_{2}z + D_{2} = 0.\)
Góc giữa \((\alpha)\) và \((\beta)\) bằng hoặc bù với góc giữa hai VTPT \(\overrightarrow{n_{\alpha}},\overrightarrow{n_{\beta}}\).
Tức là:
\(\cos\left( (\alpha),(\beta) \right) =
\left| \cos\left( \overrightarrow{n_{\alpha}},\overrightarrow{n_{\beta}}
\right) \right| = \frac{\left|
\overrightarrow{n_{\alpha}}.\overrightarrow{n_{\beta}} \right|}{\left|
\overrightarrow{n_{\alpha}} \right|.\left| \overrightarrow{n_{\beta}}
\right|}\)
\(= \frac{\left| A_{1}A_{2} + B_{1}B_{2} + C_{1}C_{2}
\right|}{\sqrt{A_{1}^{2} + B_{1}^{2} + C_{1}^{2}}.\sqrt{A_{2}^{2} +
B_{2}^{2} + C_{2}^{2}}}\)
--------------------------------------------
Hy vọng với phần tổng hợp công thức phương trình mặt phẳng trong không gian trên, bạn đã có cái nhìn rõ ràng và đầy đủ về chủ đề quan trọng này trong hình học không gian. Hãy lưu lại tài liệu để ôn tập khi cần và đừng quên luyện tập thêm các bài tập liên quan để ghi nhớ lâu hơn. Chúc bạn học tốt và đạt điểm cao trong các kỳ kiểm tra, thi THPT Quốc gia!
