Tìm m để phương trình hàm hợp, hàm ẩn chứa tham số có n nghiệm
Cách tìm m để phương trình hàm ẩn, hàm hợp có n nghiệm
Trong quá trình ôn thi THPT Quốc gia môn Toán, dạng bài tìm m để phương trình hàm hợp hoặc hàm ẩn chứa tham số có n nghiệm luôn được xem là một trong những dạng toán phân loại học sinh. Dạng này đòi hỏi khả năng kết hợp tư duy giải tích, khảo sát hàm số và phân tích số nghiệm theo tham số. Bài viết này sẽ cung cấp phương pháp tổng quát, cách lập luận nhanh, mẹo xử lý từng dạng phương trình, giúp bạn dễ dàng xác định số nghiệm và tìm điều kiện của tham số m một cách chính xác.
A. Bài tập minh họa tìm m để hàm số có n nghiệm
Ví dụ 1. Cho hàm số  \(y = f(x)\) có đồ thị như hình vẽ bên.
\(y = f(x)\) có đồ thị như hình vẽ bên.
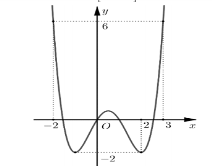
Có bao nhiêu số nguyên  \(m\)để phương trình
\(m\)để phương trình  \(f\left( x^{3} - 3x \right) = m\) có
\(f\left( x^{3} - 3x \right) = m\) có  \(6\) nghiệm phân biệt thuộc đoạn
\(6\) nghiệm phân biệt thuộc đoạn  \(\lbrack - 1;2\rbrack\)?
\(\lbrack - 1;2\rbrack\)?
A.  \(3\) B.
\(3\) B.  \(2\) C.
\(2\) C.  \(6\) D.
\(6\) D.  \(7\)
\(7\)
Hướng dẫn giải
Đặt  \(t = x^{3} - 3x\), với
\(t = x^{3} - 3x\), với  \(x \in \lbrack - 1;2\rbrack\)ta có bảng biến thiên
\(x \in \lbrack - 1;2\rbrack\)ta có bảng biến thiên
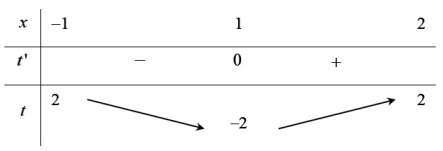
Với mỗi  \(t \in ( - 2;2\rbrack\)thì có 2 nghiệm
\(t \in ( - 2;2\rbrack\)thì có 2 nghiệm  \(x \in \lbrack -
1;2\rbrack\)
\(x \in \lbrack -
1;2\rbrack\)
Để phương trình có 6 nghiệm thì phương trình  \(f(t) = m\)có 3 nghiệm
\(f(t) = m\)có 3 nghiệm  \(t \in ( - 2;2\rbrack\)
\(t \in ( - 2;2\rbrack\)
Dựa vao đồ thị ta có  \(m = 0;m =
1\). Đáp án B.
\(m = 0;m =
1\). Đáp án B.
Lưu ý: Bài toán tìm số nghiệm của phương trình  \(f(u(x)) = m\) trên tập D.
\(f(u(x)) = m\) trên tập D.
- B1: Đặt
 \(t = u(x)\), ta khảo sát hàm
\(t = u(x)\), ta khảo sát hàm  \(t = u(x)\) trên D
\(t = u(x)\) trên D - B2: Chỉ ra sự tương ứng giữa giá trị của
 \(t\) với số giá trị của
\(t\) với số giá trị của  \(x\). Bước này quan trọng, nếu không chỉ ra được sự tương ứng thì sẽ không
\(x\). Bước này quan trọng, nếu không chỉ ra được sự tương ứng thì sẽ không - B3: Xét số nghiệm của phương trình
 \(f(t)
= m\), dựa vào B2 đưa ra kết luận.
\(f(t)
= m\), dựa vào B2 đưa ra kết luận.
Ví dụ 2. Cho hàm số  \(y = f(x)\) liên tục trên
\(y = f(x)\) liên tục trên  \(\mathbb{R}\) và có đồ thị như hình bên.
\(\mathbb{R}\) và có đồ thị như hình bên.
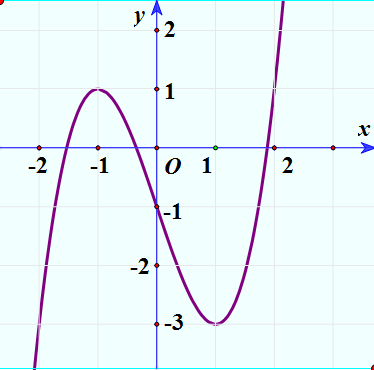
Phương trình  \(f(2sinx) =
m\) có đúng ba nghiệm phân biệt thuộc đoạn
\(f(2sinx) =
m\) có đúng ba nghiệm phân biệt thuộc đoạn  \(\lbrack - \pi;\pi\rbrack\) khi và chỉ khi
\(\lbrack - \pi;\pi\rbrack\) khi và chỉ khi
A.  \(m \in \left\{ - 3;1 \right\}\). B.
\(m \in \left\{ - 3;1 \right\}\). B.  \(m \in ( - 3;1)\).
\(m \in ( - 3;1)\).
C.  \(m \in \lbrack - 3;1)\). D.
\(m \in \lbrack - 3;1)\). D.  \(m \in ( - 3;1\rbrack\).
\(m \in ( - 3;1\rbrack\).
Hướng dẫn giải
Đặt  \(t = 2sinx\),
\(t = 2sinx\),  \(x \in \lbrack - \pi;\pi\rbrack\)
\(x \in \lbrack - \pi;\pi\rbrack\)
Ta có bảng biến thiên hàm số  \(t = g(x) =
2sinx\) trên
\(t = g(x) =
2sinx\) trên  \(\lbrack -
\pi;\pi\rbrack\).
\(\lbrack -
\pi;\pi\rbrack\).

Từ BBT ta thấy:
+  \(t \in ( - 2;0) \cup (0;2)\), mỗi
\(t \in ( - 2;0) \cup (0;2)\), mỗi  \(t\) cho 2 giá trị
\(t\) cho 2 giá trị  \(x\)
\(x\)
+  \(t \in \{ - 2;2\}\), mỗi
\(t \in \{ - 2;2\}\), mỗi  \(t\) cho 1 giá trị
\(t\) cho 1 giá trị  \(x\)
\(x\)
+  \(t = 0\), cho 3 giá trị
\(t = 0\), cho 3 giá trị  \(x\)
\(x\)
Phương trình  \(f(2sinx) = m\) có đúng ba nghiệm phân biệt thuộc đoạn
\(f(2sinx) = m\) có đúng ba nghiệm phân biệt thuộc đoạn  \(\lbrack
- \pi;\pi\rbrack\) khi và chỉ khi phương trình
\(\lbrack
- \pi;\pi\rbrack\) khi và chỉ khi phương trình  \(f(t) = m\) có:
\(f(t) = m\) có:
+ Một nghiệm duy nhất  \(t = 0\), các nghiệm còn lại không thuộc
\(t = 0\), các nghiệm còn lại không thuộc  \(\lbrack -
2;2\rbrack\), khi đó
\(\lbrack -
2;2\rbrack\), khi đó  \(m \in
\varnothing\)
\(m \in
\varnothing\)
+ Hoặc một nghiệm  \(t = 2\) nghiệm còn lại thuộc
\(t = 2\) nghiệm còn lại thuộc  \(( - 2;2)\backslash\left\{ 0
\right\}\), khi đó
\(( - 2;2)\backslash\left\{ 0
\right\}\), khi đó  \(m = 1\)
\(m = 1\)
+ Hoặc một nghiệm  \(t = - 2\), nghiệm còn lại thuộc
\(t = - 2\), nghiệm còn lại thuộc  \(( -
2;2)\backslash\left\{ 0 \right\}\), khi đó
\(( -
2;2)\backslash\left\{ 0 \right\}\), khi đó  \(m = - 3\).
\(m = - 3\).
Vậy  \(m \in \left\{ - 3;1
\right\}\). Đáp án A.
\(m \in \left\{ - 3;1
\right\}\). Đáp án A.
Ví dụ 3. Cho hàm số  \(y = f(x)\) liên tục trên
\(y = f(x)\) liên tục trên  \(\mathbb{R}\) có đồ thị như hình vẽ.
\(\mathbb{R}\) có đồ thị như hình vẽ.
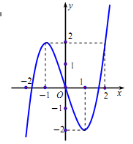
Có bao nhiêu giá trị nguyên của tham số  \(m\) để phương trình
\(m\) để phương trình  \(f\left( \sqrt{2f(cosx)} \right) = m\) có nghiệm
\(f\left( \sqrt{2f(cosx)} \right) = m\) có nghiệm  \(x \in \left\lbrack \frac{\pi}{2};\pi
\right)\).
\(x \in \left\lbrack \frac{\pi}{2};\pi
\right)\).
A.  \(5\). B.
\(5\). B.  \(3\). C.
\(3\). C.  \(2\). D.
\(2\). D.  \(4\).
\(4\).
Hướng dẫn giải
Từ hình vẽ, đặt \(f(x) = ax^{3} + bx^{2} +
cx + d\ ,(a \neq 0).\) Đồ thị hàm số đi qua gốc tọa độ
\(f(x) = ax^{3} + bx^{2} +
cx + d\ ,(a \neq 0).\) Đồ thị hàm số đi qua gốc tọa độ  \(O\) nên
\(O\) nên  \(d =
0\). Ta có hệ phương trình
\(d =
0\). Ta có hệ phương trình  \(\left\{
\begin{matrix}
- a + b - c = 2 \\
a + b + c = - 2 \\
4a + 2b + c = 1
\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}
a = 1 \\
b = 0 \\
c = - 3
\end{matrix} \right.\ .\) Do đó
\(\left\{
\begin{matrix}
- a + b - c = 2 \\
a + b + c = - 2 \\
4a + 2b + c = 1
\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}
a = 1 \\
b = 0 \\
c = - 3
\end{matrix} \right.\ .\) Do đó  \(f(x)
= x^{3} - 3x.\)
\(f(x)
= x^{3} - 3x.\)
Đặt  \(t = cosx,\ x \in \left\lbrack
\frac{\pi}{2};\pi \right) \Rightarrow t \in ( - 1;0\rbrack \Rightarrow
f(cosx) = f(t) = t^{3} - 3t\) với
\(t = cosx,\ x \in \left\lbrack
\frac{\pi}{2};\pi \right) \Rightarrow t \in ( - 1;0\rbrack \Rightarrow
f(cosx) = f(t) = t^{3} - 3t\) với  \(t
\in ( - 1;0\rbrack\).
\(t
\in ( - 1;0\rbrack\).
 \(f'(t) = 3t^{2} - 3 < 0,\ \forall t
\in ( - 1;0\rbrack \Rightarrow f(t)\) nghịch biến trên
\(f'(t) = 3t^{2} - 3 < 0,\ \forall t
\in ( - 1;0\rbrack \Rightarrow f(t)\) nghịch biến trên  \(( - 1;0\rbrack \Rightarrow 2f(t) \in \left\lbrack
2f(0);\ 2f( - 1) \right)\)
\(( - 1;0\rbrack \Rightarrow 2f(t) \in \left\lbrack
2f(0);\ 2f( - 1) \right)\)
hay  \(2f(t) \in \lbrack 0;\ 4)\). Đặt
\(2f(t) \in \lbrack 0;\ 4)\). Đặt  \(u = \sqrt{2f(t)} \Rightarrow u \in
\lbrack 0;2) \Rightarrow m = f(u) = u^{3} - 3u\) với
\(u = \sqrt{2f(t)} \Rightarrow u \in
\lbrack 0;2) \Rightarrow m = f(u) = u^{3} - 3u\) với  \(u \in \lbrack 0;2)\).
\(u \in \lbrack 0;2)\).
Ta có  \(f'(u) = 3u^{2} - 3 \Rightarrow
f'(u) = 0 \Leftrightarrow u = 1 \in \lbrack 0;2)\).
\(f'(u) = 3u^{2} - 3 \Rightarrow
f'(u) = 0 \Leftrightarrow u = 1 \in \lbrack 0;2)\).
Bảng biến thiên của  \(f(u)\).
\(f(u)\).
Từ bảng biến thiên suy ra phương trình có nghiệm  \(\Leftrightarrow - 2 \leq m < 2\).
\(\Leftrightarrow - 2 \leq m < 2\).  \(\Rightarrow \left\{ \begin{matrix}
m \in \lbrack - 2;2) \\
m \in \mathbb{Z}
\end{matrix} \right.\ \Leftrightarrow m \in \left\{ - 2; - 1;0;1
\right\}.\)Chọn D.
\(\Rightarrow \left\{ \begin{matrix}
m \in \lbrack - 2;2) \\
m \in \mathbb{Z}
\end{matrix} \right.\ \Leftrightarrow m \in \left\{ - 2; - 1;0;1
\right\}.\)Chọn D.
Lưu ý: Dạng bài toán tìm tham số  \(m\) để phương trình
\(m\) để phương trình  \(f(u(x)) = m\) có nghiệm trên D
\(f(u(x)) = m\) có nghiệm trên D
- B1: Đặt
 \(t = u(x)\) ta chỉ cần tìm miền giá trị của hàm hàm
\(t = u(x)\) ta chỉ cần tìm miền giá trị của hàm hàm  \(u(x)\) trên D. giả sử
\(u(x)\) trên D. giả sử  \(u(x) \in K,\forall x \in
D\)
\(u(x) \in K,\forall x \in
D\) - B2: Tìm tham số
 \(m\) để PT
\(m\) để PT  \(f(t) = m\) có nghiệm trên tập K. Tương đương với
\(f(t) = m\) có nghiệm trên tập K. Tương đương với  \(m\) thuộc miền giá trị của
\(m\) thuộc miền giá trị của  \(f\) trên K.
\(f\) trên K.
Nhận xét: Cho phương trình  \(f(u(x)) =
m\), nếu bài toán về số nghiệm sẽ phức tạp hơn so với bài toán có nghiệm.
\(f(u(x)) =
m\), nếu bài toán về số nghiệm sẽ phức tạp hơn so với bài toán có nghiệm.
B. Bài tập vận dụng có đáp án chi tiết
Bài tập 1. Cho hàm số  \(y = f(x)\) có đồ thị như hình vẽ.
\(y = f(x)\) có đồ thị như hình vẽ.
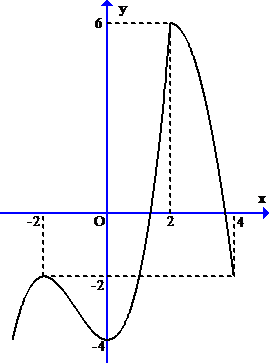
Có bao nhiêu số nguyên  \(m\) để phương trình
\(m\) để phương trình  \(\frac{1}{3}f\left( \frac{x}{2}
+ 1 \right) + x = m\) có nghiệm thuộc đoạn
\(\frac{1}{3}f\left( \frac{x}{2}
+ 1 \right) + x = m\) có nghiệm thuộc đoạn  \(\lbrack - 2\ ;\ 2\rbrack\)?
\(\lbrack - 2\ ;\ 2\rbrack\)?
A.  \(11\) B.
\(11\) B.  \(9\) C.
\(9\) C.  \(8\) D.
\(8\) D.  \(10\)
\(10\)
Bài tập 2. Cho hai hàm số  \(y =
f(x)\) và
\(y =
f(x)\) và  \(y = g(x)\) là các hàm xác định và liên tục trên
\(y = g(x)\) là các hàm xác định và liên tục trên  \(\mathbb{R}\) và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là đồ thị của hàm số
\(\mathbb{R}\) và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là đồ thị của hàm số  \(y = f(x)\)).
\(y = f(x)\)).
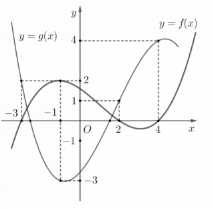
Có bao nhiêu số nguyên  \(m\) để phương trình
\(m\) để phương trình  \(f\left( 1 - g(2x - 1) \right) = m\) có nghiệm thuộc đoạn
\(f\left( 1 - g(2x - 1) \right) = m\) có nghiệm thuộc đoạn  \(\left\lbrack -
1;\frac{5}{2} \right\rbrack\).
\(\left\lbrack -
1;\frac{5}{2} \right\rbrack\).
A.  \(8\) B.
\(8\) B.  \(3\) C.
\(3\) C.  \(6\) D.
\(6\) D.  \(4\)
\(4\)
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
----------------------------------
Trong quá trình ôn thi THPT Quốc gia môn Toán, dạng bài tìm m để phương trình hàm hợp hoặc hàm ẩn chứa tham số có n nghiệm luôn được xem là một trong những dạng toán phân loại học sinh. Dạng này đòi hỏi khả năng kết hợp tư duy giải tích, khảo sát hàm số và phân tích số nghiệm theo tham số. Bài viết này sẽ cung cấp phương pháp tổng quát, cách lập luận nhanh, mẹo xử lý từng dạng phương trình, giúp bạn dễ dàng xác định số nghiệm và tìm điều kiện của tham số m một cách chính xác.










