Cho đồ thị hàm số tìm số nghiệm của phương trình f(u(x)) = a
Tìm số nghiệm của phương trình f(u(x)) = a từ đồ thị
Trong quá trình ôn thi THPT Quốc gia môn Toán, dạng bài Cho đồ thị hàm số, tìm số nghiệm của phương trình f(u(x)) = a xuất hiện rất thường xuyên và đòi hỏi khả năng đọc – hiểu đồ thị kết hợp biến đổi hàm hợp. Đây là dạng bài kiểm tra trực tiếp kỹ năng phân tích đồ thị, xác định giá trị hàm số và giải phương trình thông qua hình học trực quan. Bài viết này sẽ cung cấp phương pháp nhanh, cách suy luận chuẩn xác và ví dụ minh họa giúp học sinh nắm chắc dạng toán để tự tin chinh phục điểm cao trong đề thi.
A. PHƯƠNG PHÁP GIẢI TOÁN
Bài toán tổng quát: Cho đồ thị hoặc BBT của hàm số ![]() \(y = f(x)\) , tìm số nghiệm của các phương trình có dạng
\(y = f(x)\) , tìm số nghiệm của các phương trình có dạng ![]() \(f(x) = a\),
\(f(x) = a\), ![]() \(f\left( u(x) \right) = a\).
\(f\left( u(x) \right) = a\).
Cách giải: Ta sử dụng tính chất sau:
-
Nếu hàm số
 \(f\) đơn điệu trên khoảng
\(f\) đơn điệu trên khoảng  \((\alpha;\beta)\) và
\((\alpha;\beta)\) và  \(a\) là giá trị trung gian giữa
\(a\) là giá trị trung gian giữa  \(f(\alpha)\) và
\(f(\alpha)\) và  \(f(\beta)\) thì phương trình
\(f(\beta)\) thì phương trình  \(f(x) = a\) có nghiệm duy nhất.
\(f(x) = a\) có nghiệm duy nhất. -
Nếu phương trình
 \(f(x) = 0\) có nghiệm là
\(f(x) = 0\) có nghiệm là  \(\alpha\) thì phương trình
\(\alpha\) thì phương trình  \(f(u(x)) = 0\) có nghiệm là nghiệm phương trình
\(f(u(x)) = 0\) có nghiệm là nghiệm phương trình  \(u(x) =
\alpha\).
\(u(x) =
\alpha\).
B. BÀI TẬP MINH HỌA TÌM M ĐỂ PHƯƠNG TRÌNH CÓ N NGHIỆM
Ví dụ 1. Cho hàm số ![]() \(y = f(x)\) xác định, liên tục trên
\(y = f(x)\) xác định, liên tục trên ![]() \(\mathbb{R}\) và có bảng biến thiên như sau:
\(\mathbb{R}\) và có bảng biến thiên như sau:
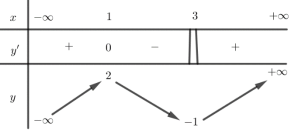
Số nghiệm của phương trình ![]() \(f(x) + 1 =
0\) là:
\(f(x) + 1 =
0\) là:
A. ![]() \(3\). B.
\(3\). B. ![]() \(0\). C.
\(0\). C. ![]() \(1\). D.
\(1\). D. ![]() \(2\).
\(2\).
Lời giải
Ta có phương trình ![]() \(f(x) + 1 = 0
\Leftrightarrow f(x) = - 1\).
\(f(x) + 1 = 0
\Leftrightarrow f(x) = - 1\).
Từ bảng biến thiên hàm số ![]() \(f(x)\) ta thấy phương trình có 2 nghiệm.
\(f(x)\) ta thấy phương trình có 2 nghiệm.
Đáp án D.
Ví dụ 2. Cho hàm số ![]() \(y = f(x)\) có bảng biến thiên sau:
\(y = f(x)\) có bảng biến thiên sau:
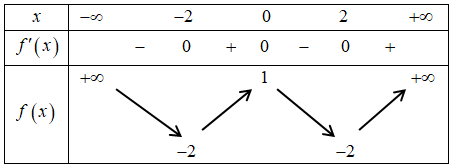
Số nghiệm của phương trình ![]() \(f(x + 1) =
0\) là
\(f(x + 1) =
0\) là
A. 0. B. 4. C. ![]() \(2\). D.
\(2\). D. ![]() \(1\).
\(1\).
Lời giải
Nhận xét: Số nghiệm của phương trình ![]() \(f(x
+ 1) = 0\) là số nghiệm của phương trình
\(f(x
+ 1) = 0\) là số nghiệm của phương trình ![]() \(f(x) = 0\).
\(f(x) = 0\).
Dựa vào BBT ta thấy số nghiệm của phương trình là 4.
Đáp án B
Ví dụ 3. Cho hàm số ![]() \(y = f(x)\) xác định trên
\(y = f(x)\) xác định trên ![]() \(\mathbb{R}\backslash\left\{ 0
\right\}\) có bảng biến thiên như sau:
\(\mathbb{R}\backslash\left\{ 0
\right\}\) có bảng biến thiên như sau:
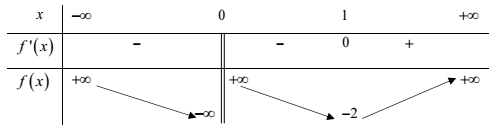
Số nghiệm của phương trình ![]() \(2f(3x - 5) - 7
= 0\) là
\(2f(3x - 5) - 7
= 0\) là
A. ![]() \(1\). B.
\(1\). B. ![]() \(2\). C.
\(2\). C. ![]() \(3\). D.
\(3\). D. ![]() \(4\).
\(4\).
Lời giải
Ta có phương trình:
![]() \(2f(3x - 5) - 7 = 0 \Leftrightarrow f(3x -
5) = \frac{7}{2}\).
\(2f(3x - 5) - 7 = 0 \Leftrightarrow f(3x -
5) = \frac{7}{2}\).
Đặt ![]() \(t = 3x - 5\), phương trình trở thành
\(t = 3x - 5\), phương trình trở thành ![]() \(f(t) = \frac{7}{2}\).
\(f(t) = \frac{7}{2}\).
Với mỗi nghiệm ![]() \(t\) thì có một nghiệm
\(t\) thì có một nghiệm ![]() \(x = \frac{t + 5}{3}\) nên số nghiệm
\(x = \frac{t + 5}{3}\) nên số nghiệm ![]() \(t\) của phương trình
\(t\) của phương trình ![]() \(f(t) = \frac{7}{2}\) bằng số nghiệm của phương trình
\(f(t) = \frac{7}{2}\) bằng số nghiệm của phương trình ![]() \(2f(3x - 5) - 7 =
0\).
\(2f(3x - 5) - 7 =
0\).
Dựa vào bảng biến thiên của hàm số ![]() \(y =
f(x)\) suy ra phương trình
\(y =
f(x)\) suy ra phương trình ![]() \(f(t) =
\frac{7}{2}\) có
\(f(t) =
\frac{7}{2}\) có ![]() \(3\) nghiệm phân biệt nên phương trình
\(3\) nghiệm phân biệt nên phương trình ![]() \(2f(3x - 5) - 7 =
0\) có
\(2f(3x - 5) - 7 =
0\) có ![]() \(3\) nghiệm phân biệt.
\(3\) nghiệm phân biệt.
Chọn C.
C. BÀI TẬP VẬN DỤNG CÓ ĐÁP ÁN CHI TIẾT
Bài tập 1. Cho hàm số ![]() \(y = f(x)\) có bảng biến thiên như sau:
\(y = f(x)\) có bảng biến thiên như sau:
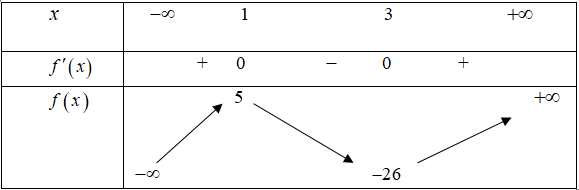
Đồ thị hàm số ![]() \(y = f\left( x^{2} - 4x + 5
\right)\) cắt trục hoành tại bao nhiêu điểm?
\(y = f\left( x^{2} - 4x + 5
\right)\) cắt trục hoành tại bao nhiêu điểm?
A. 2. B. 3 C. 4 D. 5.
Bài tập 2. Cho hàm số ![]() \(f(x)\) liên tục trên
\(f(x)\) liên tục trên ![]() \(\mathbb{R}\) có đồ thị
\(\mathbb{R}\) có đồ thị ![]() \(y = f(x)\) như hình vẽ bên.
\(y = f(x)\) như hình vẽ bên.
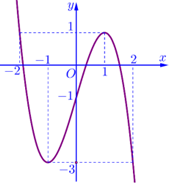
Phương trình ![]() \(f\left( f(x) \right) = - 2\) có tất cả bao nhiêu nghiệm dương phân biệt.
\(f\left( f(x) \right) = - 2\) có tất cả bao nhiêu nghiệm dương phân biệt.
A. 3. B. 4. C. 6. D. 7.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
-------------------------------
Dạng toán tìm số nghiệm của phương trình f(u(x)) = a từ đồ thị đòi hỏi sự cẩn thận, quan sát tinh tế và kỹ năng triển khai hợp lý các bước phân tích. Hy vọng nội dung bài viết đã giúp bạn hiểu đúng bản chất, biết cách xử lý từng trường hợp và làm chủ phương pháp tư duy để giải nhanh trong phòng thi. Hãy tiếp tục luyện tập với các bài giảng và chuyên đề khác để nâng cao tốc độ và độ chính xác trong môn Toán THPT Quốc gia.









