Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập phương trình mặt phẳng Toán 12 Có lời giải chi tiết

Ôn thi THPT Quốc gia môn Toán

Phương trình mặt phẳng lớp 12

Phương trình mặt phẳng là một trong những chuyên đề quan trọng của chương trình Toán lớp 12, đặc biệt trong phần hình học không gian. Để học tốt và làm chủ dạng toán này, học sinh cần luyện tập thường xuyên với các bài tập phương trình mặt phẳng trong không gian oxyz có lời giải chi tiết nhằm hiểu bản chất và phương pháp giải. Trong bài viết này, chúng tôi cung cấp tuyển chọn các bài tập từ cơ bản đến nâng cao, được trình bày rõ ràng, dễ hiểu, giúp bạn nắm chắc kiến thức, rèn luyện kỹ năng giải bài và sẵn sàng cho các kỳ kiểm tra, thi THPT Quốc gia. Cùng bắt đầu ôn luyện hiệu quả ngay hôm nay!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 31 câu
  • Điểm số bài kiểm tra: 31 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Chọn đáp án thích hợp

    Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1; - 2;1), B( - 1;3;3), C(2; - 4;2). Một vectơ pháp tuyến \overrightarrow{n} của mặt phẳng (ABC) là:

    Hướng dẫn:

    Phưowng pháp tự luận

    Ta có \overrightarrow{AB} = ( - 2;5;2), \overrightarrow{AC} = (1; - 2;1)

    \Rightarrow \overrightarrow{n} = \left\lbrack \overrightarrow{AB},\overrightarrow{AC} \right\rbrack = (9;4; - 1).

    Phương pháp trắc nghiệm

    Sử dụng MTBT tính tích có hướng.

    Có \overrightarrow{AB} = ( - 2;5;2), \overrightarrow{AC} = (1; - 2;1).

    Chuyển sang chế độ Vector: Mode 8.

    Ấn tiếp 1 – 1: Nhập tọa độ \overrightarrow{AB} vào vector A.

    Sau đó ấn AC. Shift – 5 – 1 – 2 – 1 Nhập tọa độ \overrightarrow{AC} vào vector B.

    Sau đó ấn AC.

    Để nhân \left\lbrack \overrightarrow{AB},\overrightarrow{AC} \right\rbrack ấn Shift – 5 –3 – X Shift - 5 – 4 - =

  • Câu 2: Nhận biết
    Chọn đáp án chính xác

    Trong không gian với hệ trục toạ độ Oxyz. Biết A,B,C là số thực khác 0, mặt phẳng chứa trục Oz có phương trình là:

    Hướng dẫn:

    Trục Oz là giao tuyến của 2 mặt phẳng (Ozx),(Oyz) nên mặt phẳng chứa Oz thuộc chùm mặt phẳng tạo bởi 2 mặt (Ozx),(Oyz) \Rightarrow Ax + By = 0

    Vậy Ax + By = 0.

  • Câu 3: Nhận biết
    Xác định phương trình thỏa mãn điều kiện

    Trong không gian với hệ trục toạ độ Oxyz. Phương trình mặt phẳng qua A(2;5;1) và song song với mặt phẳng (Oxy) là:

    Hướng dẫn:

    Phương pháp tự luận

    Mặt phẳng qua A(2;5;1) và có vectơ pháp tuyến \overrightarrow{k} = (0;0;1) có phương trình: z - 1 = 0.

    Phương pháp trắc nghiệm

    Mặt phẳng qua A và song song với (Oxy) có phương trình z = z_{A}.

  • Câu 4: Nhận biết
    Tìm khẳng định đúng

    Chọn khẳng định đúng

    Hướng dẫn:

    Câu đúng là: Nếu hai mặt phẳng song song thì hai vectơ pháp tuyến tương ứng cùng phương

  • Câu 5: Thông hiểu
    Chọn đáp án đúng

    Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(5;1;3),B(1;2;6),C(5;0;4),D(4;0;6). Viết phương trình mặt phẳng qua D và song song với mặt phẳng (ABC).

    Hướng dẫn:

    Phương pháp tự luận

    +)\overrightarrow{AB} = ( - 4;1;3),\ \ \overrightarrow{AC} = (0; - 1;1) \Rightarrow \left\lbrack \overrightarrow{AB},\overrightarrow{AC} \right\rbrack = (4;4;4).

    +) Mặt phẳng đi qua Dcó VTPT \overrightarrow{n} = (1;1;1)có phương trình: x + y + z - 10 = 0.

    +) Thay tọa độ điểm A vào phương trình mặt phẳng thấy không thỏa mãn.

    Vậy phương trình mặt phẳng thỏa mãn yêu cầu bài toán là: x + y + z - 10 = 0.

    Phương pháp trắc nghiệm

    Gọi phương trình mặt phẳng(ABC) có dạng Ax + By + Cz + D = 0.

    Sử dụng MTBT giải hệ bậc nhất 3 ẩn, nhập tọa độ 3 điểmA,B,Cvào hệ, chọn D = 1 ta được A = \frac{1}{9},B = \frac{1}{9},C = \frac{1}{9}. (Trong trường hợp chọn D = 1 vô nghiệm ta chuyển sang chọn D = 0).

    Suy ra mặt phẳng(ABC) có VTPT \overrightarrow{n} = (1;1;1)

    Mặt phẳng đi qua Dcó VTPT \overrightarrow{n} = (1;1;1)có phương trình: x + y + z - 10 = 0.

    Thay tọa độ điểm A vào phương trình mặt phẳng thấy không thỏa mãn.

  • Câu 6: Thông hiểu
    Tìm khẳng định đúng

    Trong không gian với hệ trục toạ độ Oxyz, cho điểm A( - 1;2;1) và hai mặt phẳng (\alpha):2x + 4y - 6z - 5 = 0 và (\beta):x + 2y - 3z = 0. Tìm khẳng định đúng?

    Hướng dẫn:

    Có \overrightarrow{n_{\alpha}} = (2;4; - 6), \overrightarrow{n_{\beta}} = (1;2; - 3) \Rightarrow (\alpha)//(\beta)

    Và A \in (\beta)

  • Câu 7: Thông hiểu
    Chọn đáp án đúng

    Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2; - 1;1),\ B(1;0;4)và C(0; - 2; - 1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:

    Hướng dẫn:

    Ta có: \overrightarrow{CB}(1;2;5).

    Mặt phẳng qua A và vuông góc với đường thẳng BCcó một VTPT là \overrightarrow{CB}(1;2;5)nên có phương trình là: x + 2y + 5z - 5 = 0.

    Vậy x + 2y + 5z - 5 = 0.

  • Câu 8: Nhận biết
    Xác định vecto pháp tuyến của mặt phẳng

    Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) có phương trình 3x + 2y - z + 1 = 0. Mặt phẳng (P) có một vectơ pháp tuyến là:

    Hướng dẫn:

    Mặt phẳng (P): 3x + 2y - z + 1 = 0 có một vectơ pháp tuyến \overrightarrow{n}(3;2; - 1)

  • Câu 9: Nhận biết
    Chọn đáp án đúng

    Trong không gian với hệ toạ độ Oxyz. Mặt phẳng (P) là - x + 3z - 2 = 0 có phương trình song song với:

    Hướng dẫn:

    Mặt phẳng (P) là - x + 3z - 2 = 0 có phương trình song song với trục Oy.

  • Câu 10: Nhận biết
    Tìm điểm thuộc mặt phẳng

    Trong không gian với hệ toạ độ Oxyz. Điểm nào sau đây thuộc mặt phẳng (P) - 2x + y - 5 = 0

    Hướng dẫn:

    Phương pháp tự luận

    Thay tọa độ các điểm vào phương trình mặt phẳng, nếu điểm nào làm cho vế trái bằng 0 thì đó là điểm thuộc mặt phẳng.

    Phương pháp trắc nghiệm

    Nhập phương trình mặt phẳng (P) vào máy tính dạng sau: - 2X + Y + 0A - 5 = 0, sau đó dùng hàm CALC và nhập tọa độ (x;y;z)của các điểm vào. Nếu bằng 0 thì điểm đó thuộc mặt phẳng.

  • Câu 11: Nhận biết
    Tìm tọa độ giao điểm

    Trong không gian với hệ trục tọa độ Oxyz. Tọa độ giao điểm Mcủa mặt phẳng (P):2x + 3y + z - 4 = 0 với trục Ox là?

    Hướng dẫn:

    Gọi M(a,0,0) là điểm thuộc trục Ox. Điểm M \in (P) \Rightarrow 2a - 4 = 0 \Leftrightarrow a = 2 .

    Vậy M(2,0,0) là giao điểm của (P),Ox.

    Phương pháp trắc nghiệm

    Giải hệ PT gồm PT của (P) và của (Ox): \left\{ \begin{matrix} 2x + 3y + z - 4 = 0 \\ y = 0 \\ z = 0 \\ \end{matrix} \right.; bấm máy tính.

  • Câu 12: Thông hiểu
    Chọn đáp án đúng

    Trong không gian với hệ trục tọa độ Oxyz, gọi (P)là mặt phẳng chứa trục Ox và vuông góc với mặt phẳng (Q):x + y + z - 3 = 0. Phương trình mặt phẳng (P) là:

    Hướng dẫn:

    +) Trục Ox véctơ đơn vị \overrightarrow{i} = (1;0;0).

    Mặt phẳng (Q) có VTPT {\overrightarrow{n}}_{(Q)} = (1;1;1).

    Mặt phẳng (P) chứa trục Ox và vuông góc với (Q):x + y + z - 3 = 0nên (P) có VTPT \overrightarrow{n} = \left\lbrack \overrightarrow{i},\overrightarrow{n_{(Q)}} \right\rbrack = (0; - 1;1).

    Phương trình mặt phẳng (P) là: y - z = 0.

  • Câu 13: Nhận biết
    Viết phương trình mặt phẳng

    Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(5;1;3),B(1;2;6),C(5;0;4),D(4;0;6). Viết phương trình mặt phẳng chứa AB và song song với CD.

    Hướng dẫn:

    +) \overrightarrow{AB} = ( - 4;1;3),\ \ \overrightarrow{CD} = ( - 1;0;2) \Rightarrow \left\lbrack \overrightarrow{AB},\overrightarrow{CD} \right\rbrack = (2;5;1).

    +) Mặt phẳng đi quaA có VTPT \overrightarrow{n} = (2;5;1)có phương trình là: 2x + 5y + z - 18 = 0.

    +) Thay tọa độ điểm Cvào phương trình mặt phẳng thấy không thỏa mãn.

    Vậy phương trình mặt phẳng thỏa mãn yêu cầu bài toán là: 2x + 5y + z - 18 = 0

  • Câu 14: Nhận biết
    Viết phương trình mặt phẳng (ABC)

    Trong không gian với hệ toạ độ Oxyz, cho A(a;0;0), B(0;b;0), C(0;0;c), (abc \neq 0). Khi đó phương trình mặt phẳng (ABC) là:

    Hướng dẫn:

    Phương trình mặt phẳng (ABC) cần tìm là: \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1.

  • Câu 15: Nhận biết
    Xác định phương trình mặt phẳng

    Trong không gian với hệ toạ độ Oxyz. Phương trình mặt phẳng (P) đi qua điểm A( - 1;2;0) và nhận \overrightarrow{n}( - 1;0;2) là VTPT có phương trình là:

    Hướng dẫn:

    Mặt phẳng (P) đi qua điểm A( - 1;2;0) và nhận \overrightarrow{n}( - 1;0;2) là VTPT có phương trình là:

    - 1(x + 1) + 0(y - 2) + 2(z - 0) = 0

    \Leftrightarrow - x - 1 + 2z = 0 \Leftrightarrow - x + 2z - 1 = 0.

    Vậy - x + 2z - 1 = 0.

    Phương pháp trắc nghiệm (nên có)

    Từ tọa độ VTPT suy ra hệ số B=0, vậy loại ngay đáp án - x + 2y - 5 = 0 và - x + 2y - 5 = 0

    Chọn 1 trong 2 PT còn lại bằng cách thay tọa độ điểm A vào.

  • Câu 16: Nhận biết
    Chọn khẳng định đúng

    Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (\alpha):3x - z = 0. Tìm khẳng định đúng trong các mệnh đề sau:

    Hướng dẫn:

    Khẳng định đúng là: “(\alpha) \supset Oy”

  • Câu 17: Nhận biết
    Chọn đáp án đúng

    Trong không gian với hệ trục toạ độ Oxyz. Mặt phẳng đi qua M(1;4;3) và vuông góc với trục Oy có phương trình là:

    Hướng dẫn:

    Phương pháp tự luận

    Mặt phẳng qua M(1;4;3) và có vectơ pháp tuyến \overrightarrow{j} = (0;1;0) có phương trình y - 4 = 0.

    Phương pháp trắc nghiệm

    Mặt phẳng qua M và vuông góc với trục Oy có phương trình y = y_{M}.

  • Câu 18: Nhận biết
    Tìm câu sai

    Trong không gian với hệ trục toạ độ Oxyz, cho điểm M(2; - 1;3) và các mặt phẳng: (\alpha):x - 2 = 0, (\beta):y + 1 = 0, (\gamma):z - 3 = 0. Tìm khẳng định sai.

    Hướng dẫn:

    Câu sai là: “(\alpha)//Ox”

  • Câu 19: Thông hiểu
    Xác định phương trình mặt phẳng

    Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (\alpha)đi qua A(2; - 1;4), B(3;2; - 1) và vuông góc với mặt phẳng (Q):x + y + 2z - 3 = 0. Phương trình mặt phẳng (\alpha) là:

    Hướng dẫn:

    Phương pháp tự luận

    \overrightarrow{AB} = (1;3; - 5), \overrightarrow{n_{Q}} = (1;1;2)

    Mặt phẳng (\alpha) đi qua A(2; - 1;4) và có vectơ pháp tuyến \left\lbrack \overrightarrow{AB},\overrightarrow{n_{Q}} \right\rbrack = ( - 10; - 6;8) = - 2(5;3; - 4) có phương trình: 5x + 3y - 4z + 9 = 0.

    Vậy 5x + 3y - 4z + 9 = 0.

    Phương pháp trắc nghiệm

    Do (\alpha)\bot(Q) \Rightarrow \overrightarrow{n_{\alpha}}.\overrightarrow{n_{Q}} = 0, kiểm tra mp (\alpha)nào có \overrightarrow{n_{\alpha}}.\overrightarrow{n_{Q}} = 0.

  • Câu 20: Nhận biết
    Tìm câu sai

    Chọn khẳng định sai

    Hướng dẫn:

    Câu sai: “Nếu hai đường thẳngAB,CD song song thì vectơ \left\lbrack \overrightarrow{AB},\overrightarrow{CD} \right\rbrack là một vectơ pháp tuyến của mặt phẳng (ABCD)”.

  • Câu 21: Thông hiểu
    Định phương trình mặt phẳng

    Trong không gian với hệ toạ độ Oxyz, gọi (\alpha) là mặt phẳng qua các hình chiếu của A(5;4;3)lên các trục tọa độ. Phương trình của mặt phẳng (\alpha)là:

    Hướng dẫn:

    Gọi M,\ N,\ P lần lượt là hình chiếu vuông góc của điểm A trên trục Ox,\ Oy,\ Oz.

    Ta có: M(5;0;0), N(0;4;0), P(0;0;3).

    Phương trình mặt phẳng (\alpha) qua M(5;0;0), N(0;4;0), P(0;0;3)là:

    \frac{x}{5} + \frac{y}{4} + \frac{z}{3} = 1 \Leftrightarrow 12x + 15y + 20z - 60 = 0.

    Vậy 12x + 15y + 20z - 60 = 0.

  • Câu 22: Thông hiểu
    Chọn đáp án đúng

    Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A( - 1;0;1),B( - 2;1;1). Phương trình mặt phẳng trung trực của đoạn AB là:

    Hướng dẫn:

    Phương pháp tự luận

    +) \overrightarrow{AB} = ( - 1;1;0).

    +) Trung điểm I của đoạnAB là I(\frac{- 3}{2};\frac{1}{2};1)

    Mặt phẳng trung trực của đọan AB là- (x + \frac{3}{2}) + (y - \frac{1}{2}) = 0 hay x - y + 2 = 0.

    Phương pháp trắc nghiệm

    Do (\alpha) là mặt phẳng trung trực của AB nên (\alpha)\bot AB

    Kiểm tra mặt phẳng (\alpha) nào có \overrightarrow{n_{\alpha}} = k\overrightarrow{AB}và chứa điểm I

    Cả 4 đáp án đều thỏa điều kiện \overrightarrow{n_{\alpha}} = k\overrightarrow{AB}.

    Cả 4 PT đều chung dạng: x–y+0z+D=0, nên để kiếm tra PT nào thỏa tọa độ điểm I ta bấm máy tính: 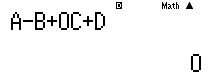trong đó nhập A, B, C là tọa độ I, còn D là số hạng tự do từng PT, nếu cái nào làm bằng 0 thì chọn.

  • Câu 23: Nhận biết
    Tìm khẳng định sai

    Chọn khẳng định sai

    Hướng dẫn:

    Câu sai: “Nếu \overrightarrow{n} là một vectơ pháp tuyến của mặt phẳng (P) thì k\overrightarrow{n}\ \ (k\mathbb{\in R}) cũng là một vectơ pháp tuyến của mặt phẳng (P).”

  • Câu 24: Nhận biết
    Tìm vecto pháp tuyến của mặt phẳng

    Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) có phương trình - 2x + 2y - z - 3 = 0. Mặt phẳng (P) có một vectơ pháp tuyến là:

    Hướng dẫn:

    Mặt phẳng (P) có phương trình - 2x + 2y - z - 3 = 0 có một vectơ pháp tuyến \overrightarrow{n}(4; - 4;2)

  • Câu 25: Thông hiểu
    Định phương trình mặt phẳng ABC

    Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(3; - 2; - 2), B(3;2;0), C(0;2;1). Phương trình mặt phẳng (ABC) là:

    Hướng dẫn:

    Phương pháp tự luận

    \overrightarrow{AB} = (0;4;2), \overrightarrow{AC} = ( - 3;4;3)

    (ABC) qua A(3; - 2; - 2) và có vectơ pháp tuyến \left\lbrack \overrightarrow{AB},\overrightarrow{AC} \right\rbrack = (4; - 6;12) = 2(2; - 3;6)

    \Rightarrow (ABC):2x - 3y + 6z = 0

    Phương pháp trắc nghiệm

    Sử dụng MTBT tính tích có hướng.

    Hoặc thay tọa độ cả 3 điểm A, B, C vào mặt phẳng xem có thỏa hay không?

  • Câu 26: Nhận biết
    Tìm khẳng định sai

    Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (\alpha):Ax + By + Cz + D = 0. Tìm khẳng định sai trong các mệnh đề sau:

    Hướng dẫn:

    Khẳng định sai: “A \neq 0,B = 0,C \neq 0,D = 0 khi và chỉ khi (\alpha) song song với mặt phẳng (Oyz).”

  • Câu 27: Thông hiểu
    Viết phương trình mặt phẳng

    Trong không gian với hệ toạ độ Oxyz. Mặt phẳng (P) đi qua các điểm A( - 1;0;0), B(0;2;0), C(0;0; - 2) có phương trình là:

    Hướng dẫn:

    Phương pháp tự luận

    Theo công thức phương trình mặt chắn ta có: \frac{x}{- 1} + \frac{y}{2} + \frac{z}{- 2} = 1

    \Leftrightarrow - 2x + y - z - 2 = 0.

    Vậy - 2x + y - z - 2 = 0.

    Phương pháp trắc nghiệm

    Nhập phương trình mặt phẳng (P) vào máy tính, sau đó dùng hàm CALC và nhập tọa độ (x;y;z)của các điểm vào. Nếu tất cả các điểm đều cho kết quả bằng 0 thì đó đó là mặt phẳng cần tìm. Chỉ cần 1 điểm làm cho phương trình khác 0 đều loại.

  • Câu 28: Nhận biết
    Tìm khẳng định sai

    Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (\alpha):6x - 3y - 2z - 6 = 0. Khẳng định nào sau đây sai?

    Hướng dẫn:

    Do d\left( O,(\alpha) \right) = \frac{6}{\sqrt{36 + 9 + 4}} = \frac{6}{7}.

  • Câu 29: Nhận biết
    Định phương trình mặt phẳng

    Trong không gian với hệ trục tọa độ Oxyz. Phương trình của mặt phẳng chứa trục Ox và qua điểm I(2; - 3;1) là:

    Hướng dẫn:

    Trục Ox đi qua A(1;0;0) và có \overrightarrow{i} = (1;0;0)

    Mặt phẳng đi qua I(2; - 3;1) và có vectơ pháp tuyến \overrightarrow{n} = \left\lbrack \overrightarrow{i},\overrightarrow{AI} \right\rbrack = (0;1;3) có phương trình y + 3z = 0.

    Vậy y + 3z = 0.

  • Câu 30: Thông hiểu
    Viết phương trình mặt phẳng

    Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (\alpha)đi qua hai điểm A(5; - 2;0), B( - 3;4;1) và có một vectơ chỉ phương là \overrightarrow{a}(1;1;1). Phương trình của mặt phẳng (\alpha) là:

    Hướng dẫn:

    Ta có: \overrightarrow{AB}( - 8;6;1).

    Mặt phẳng (\alpha)đi qua hai điểm A(5; - 2;0), B( - 3;4;1) và có một vectơ chỉ phương là \overrightarrow{a}(1;1;1) nên có một VTPT là: \overrightarrow{n} = \left\lbrack \overrightarrow{AB},\overrightarrow{a} \right\rbrack = (5;9; - 14).

    Mặt phẳng (\alpha)đi qua điểm A(5; - 2;0) và có một VTPT \overrightarrow{n} = (5;9; - 14) có phương trình là:

    5x + 9y - 14z - 7 = 0.

    Vậy 5x + 9y - 14z - 7 = 0.

  • Câu 31: Thông hiểu
    Chọn phương án thích hợp

    Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (\alpha) đi qua M(0; - 2;3), song song với đường thẳng d:\frac{x - 2}{2} = \frac{y + 1}{- 3} = z và vuông góc với mặt phẳng (\beta):x + y - z = 0 có phương trình:

    Hướng dẫn:

    Phương pháp tự luận

    Ta có \overrightarrow{u_{d}} = (2; - 3;1), \overrightarrow{n_{\beta}} = (1;1; - 1)

    Mặt phẳng (\alpha) đi qua M(0; - 2;3) và có vectơ pháp tuyến \overrightarrow{n_{\ ^{\alpha}}} = \left\lbrack \overrightarrow{u_{d}},\overrightarrow{n_{\beta}} \right\rbrack = (2;3;5)

    \Rightarrow (\alpha):2x + 3y + 5z - 9 = 0.

    Phương pháp trắc nghiệm

    Do \left\{ \begin{matrix} (\alpha)//(d) \\ (\alpha)\bot(Q) \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} \overrightarrow{n_{\alpha}} = k\overrightarrow{n_{Q}} \\ \overrightarrow{n_{\alpha}}.\overrightarrow{n_{Q}} = 0 \\ \end{matrix} \right. kiểm tra mp (\alpha)nào thỏa hệ

0/31
31 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (61%):
    2/3
  • Thông hiểu (39%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
Tải file làm trên giấy
1
50 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này