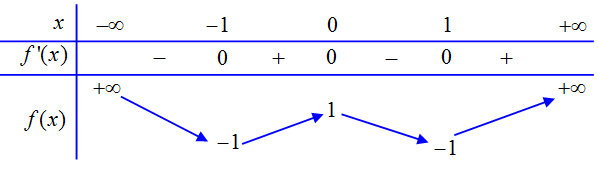
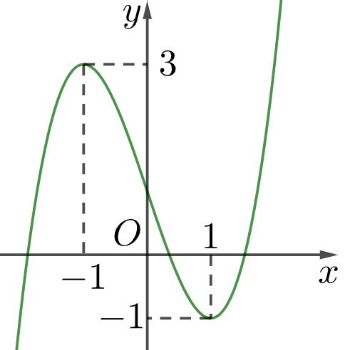
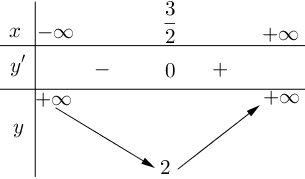
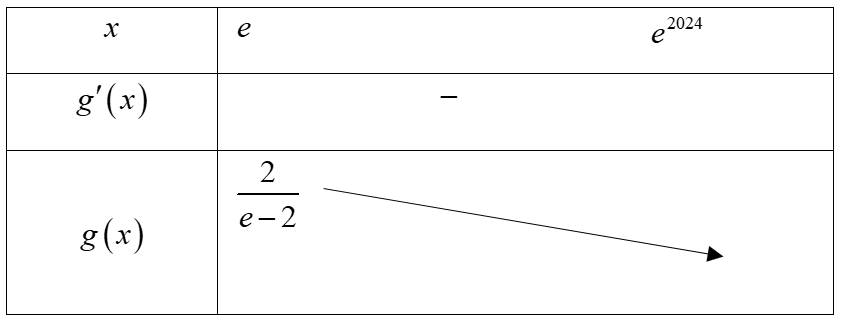
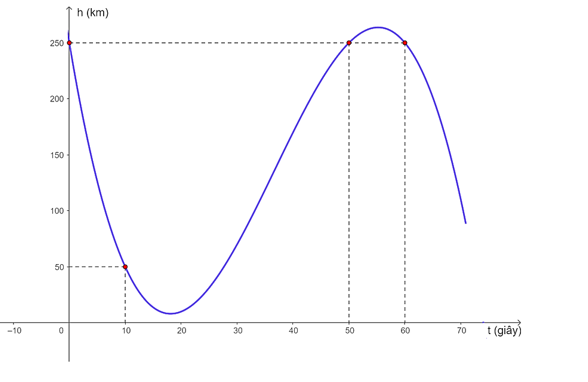
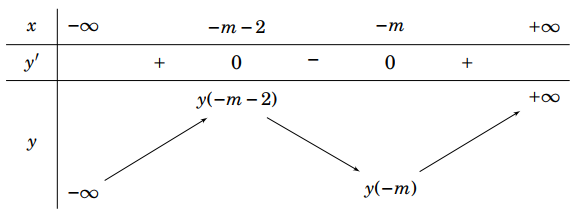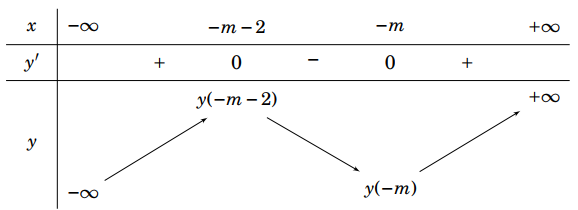Cho hàm số bậc bốn . Hàm số
có đồ thị như hình dưới đây
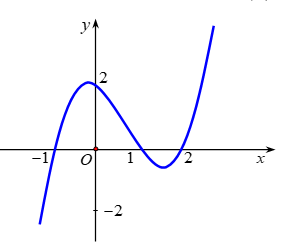
Xét tính đúng sai của các nhận định sau:
a) Hàm số đồng biến trên khoảng
. Sai||Đúng
b) Hàm số đồng biến trên khoảng
. Đúng||Sai
c) Hàm số nghịch biến trên khoảng
. Sai||Đúng
d) Hàm số nghịch biến trên khoảng
. Đúng||Sai
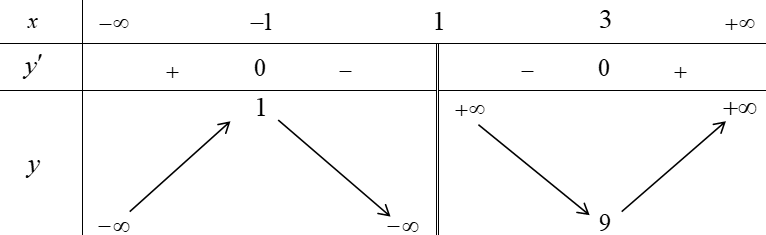
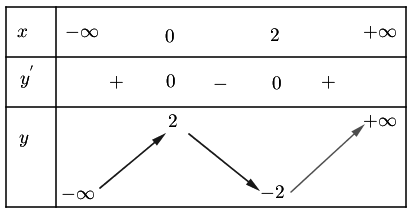
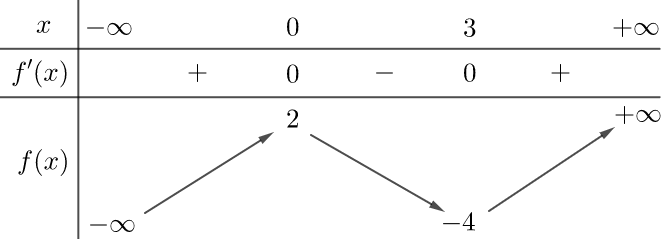
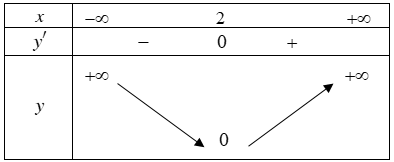
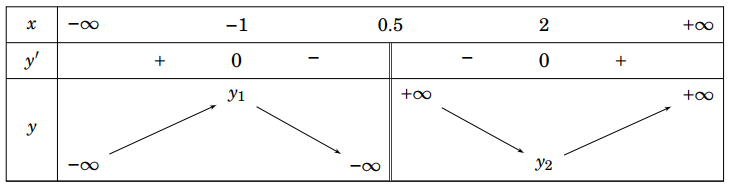
Cho hàm số bậc bốn . Hàm số
có đồ thị như hình dưới đây

Xét tính đúng sai của các nhận định sau:
a) Hàm số đồng biến trên khoảng
. Sai||Đúng
b) Hàm số đồng biến trên khoảng
. Đúng||Sai
c) Hàm số nghịch biến trên khoảng
. Sai||Đúng
d) Hàm số nghịch biến trên khoảng
. Đúng||Sai
a) Saib) Đúngc) Said) Đúng
a) Sai, vì dựa vào đồ thị thì
.
b) Đúng, vì dựa vào đồ thị thì
.
c) Sai, vì dựa vào đồ thị thì
.
d) Đúng, vì dựa vào đồ thị thì
.