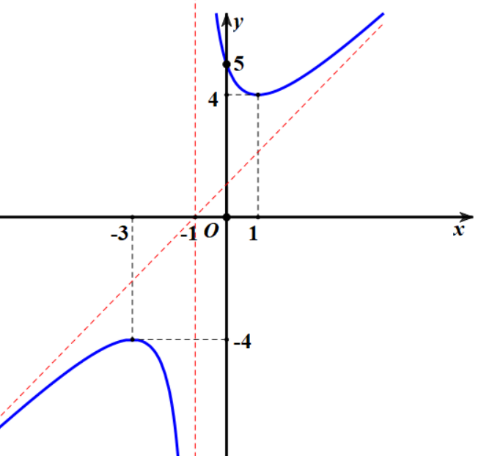
Cho hàm số có đồ thị
. Xét tính đúng sai của các khẳng định dưới đây:
a) Tập xác định của hàm số đã cho là . Sai||Đúng
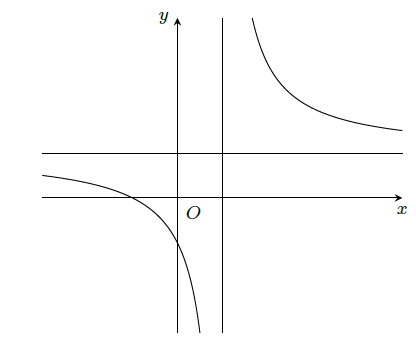
b) Đồ thị hàm số có tiệm cận đứng là đường thẳng và có tiệm cận xiên là đường thẳng
. Đúng||Sai
c) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng . Đúng||Sai
d) Cho đường thẳng . Khi đó có đúng 8 giá trị nguyên của tham số
không vượt quá 10 để đồ thị hàm số đã cho cắt đường thẳng
tại hai điểm phân biệt nằm về hai phía so với tiệm cận đứng của đồ thị
. Sai||Đúng
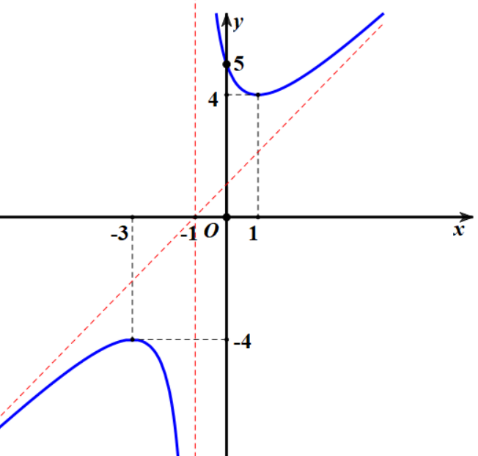
Cho hàm số có đồ thị
. Xét tính đúng sai của các khẳng định dưới đây:
a) Tập xác định của hàm số đã cho là . Sai||Đúng
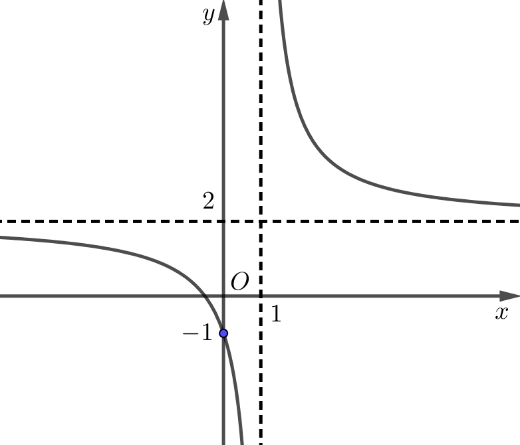
b) Đồ thị hàm số có tiệm cận đứng là đường thẳng và có tiệm cận xiên là đường thẳng
. Đúng||Sai
c) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng . Đúng||Sai
d) Cho đường thẳng . Khi đó có đúng 8 giá trị nguyên của tham số
không vượt quá 10 để đồ thị hàm số đã cho cắt đường thẳng
tại hai điểm phân biệt nằm về hai phía so với tiệm cận đứng của đồ thị
. Sai||Đúng
|
a) Sai |
b) Đúng |
c) Đúng |
d) Sai |
a) SAI vì Tập xác định của hàm số đã cho là .
b) ĐÚNG. Dễ thấy tiệm cận đứng là .
Ta có
.
Vậy phương trình tiệm cận xiên là .
c) ĐÚNG. Ta có .
Ta thấy .
.
Vậy tổng các giá trị cực đại và giá trị cực tiểu là .
d) SAI. Phương trình hoành độ giao điểm
Dễ thấy phương trình không có nghiệm nên phương trình tương đương
.
Nếu thì phương trình có nghiệm duy nhất
.
Nếu , phương trình đã cho có hai nghiệm
.
Yêu cầu bài toán tương đương .
Vậy có 9 giá trị nguyên của tham số thỏa mãn là
.