Một vật rơi tự do có phương trình chuyển động là , trong đó
. Tìm vận tốc tức thời của vật tại thời điểm
.
Ta có: .
Vận tốc tức thời của vật tại thời điểm là:
.
Việc vận dụng đạo hàm để giải quyết các bài toán thực tiễn là một trong những nội dung quan trọng trong chương trình Toán lớp 12. Đây không chỉ là phần kiến thức nền tảng giúp học sinh ôn thi THPT Quốc gia hiệu quả mà còn rèn luyện kỹ năng tư duy logic, phân tích và giải quyết vấn đề thực tế. Trong bài viết này, chúng tôi tổng hợp các dạng bài tập Toán 12 ứng dụng đạo hàm thường gặp nhất, có đầy đủ lời giải chi tiết, phương pháp tư duy kèm ví dụ minh họa cụ thể. Tài liệu phù hợp với học sinh lớp 12 ôn thu THPT Quốc gia môn Toán.
Một vật rơi tự do có phương trình chuyển động là , trong đó
. Tìm vận tốc tức thời của vật tại thời điểm
.
Ta có: .
Vận tốc tức thời của vật tại thời điểm là:
.
Trên mặt phẳng tọa độ (Oxy), cho điểm Một đường thẳng đi qua A cắt trục hoành tại B, cắt trục tung tại C tạo thành một tam giác OBC, với O là gốc tọa độ (tham khảo hình vẽ).
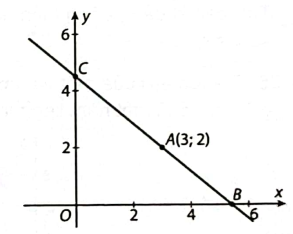
Tìm toạ độ điểm để diện tích tam giác OBC là nhỏ nhất.
+ Đường thằng qua và
có phương trinh
. Hay
.
Vậy điểm có tung độ là
.
Diện tích tam giác OBC là .
+ Khảo sát sự biến thiên của hàm số .
Tập xác đỉnh: .
Sự biến thiên: Ta có .
- (do
).
- Hàm số nghịch biến trên khoảng (3; 6), đồng biến trên khoảng
.
- Hàm số đạt cực tiểu tại với
.
- Giới hạn vô cực: , giới hạn tại vô cực:
.
- Bảng biến thiên:
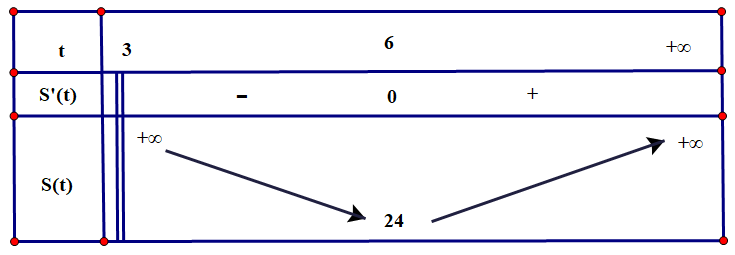
Diện tích tam giác OBC nhỏ nhất với điểm .
Giả sử chi phí để sản xuất
máy vô tuyến là
.
Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ sản phẩm lên
sản phẩm. Hỏi chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 90 sản phẩm lên 91 sản phẩm bằng bao nhiêu?
Xét là số gia của biến số tại điểm
.
Ta có:
.
Ta thấy: .
Vậy hàm chi phí biên là: .
Ta có:.
Dựa vào kết quả đó, ta thấy chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 90 sản phẩm lên 91 sản phẩm là .
Số dân của một thị trấn sau năm kể từ năm
được ước tính bởi công thức
được tính bằng nghìn người).

Hỏi trong khoảng thời gian từ năm đến năm
dân số của thị trấn đạt giá trị lớn nhất bằng bao nhiêu?
Xét hàm số với
suy ra
.
Suy ra hàm số đồng biến trên đoạn
.
Vậy dân số đạt giá trị lớn nhất bằng .
Một chuyển động thẳng xác định bởi phương trình , trong đó
tính bằng mét và
là thời gian tính bằng giây. Tính vận tốc tức thời tại thời điểm
.
Ta có .
Vận tốc tức thời tại thời điểm là
.
Giả sử chi phí để sản xuất sản phẩm của một nhà máy được cho bởi
(triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là
. Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?
Khảo sát sự biến thiên của hàm số .
Tập xác định: .
Sự biến thiên: Ta có .
- (do
).
- Hàm số đồng biến trên khoảng
, nghịch biến trên khoàng
.
- Hàm số đạt cực tiều tại
với
.
- Giới hạn tại vô cực: .
Bảng biến thiên:
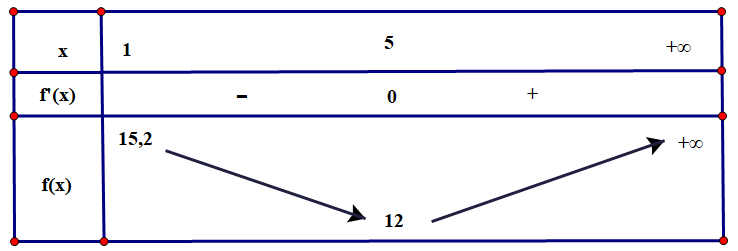
Số lượng sản phẩm cần sản xuất là để chi phí trung bình là thấp nhất
Giả sử chi phí để sản xuất đơn vị hàng hóa nào đó là
. Khi đó hàm chi phí biên tương ứng là
Hàm chi phí biên tương ứng là: .
Một vật chuyển động có quãng đường được xác định bởi phương trình , trong đó
tính bằng mét và
là thời gian tính bằng giây. Tính vận tốc tức thời tại thời điểm
.
Ta có
Một bể ban đầu chứa lít nước. Sau đó, cứ mỗi phút người ta bơm thêm
lít nước, đồng thời cho vào bể
gam chất khử trùng. Đặt
gam/lít là nồng độ chất khử trùng trong bể sau
phút , biết rằng sau khi khảo sát sự biến thiên của hàm số
, ta thấy giá trị
tăng theo
nhưng không vượt ngưỡng
gam/lít. Tìm số
.
Sau phút, trong bể chứa
lít nước và
gam chất khử trùng.
Suy ra nồng độ chất khử trùng trong bể sau phút là
gam/lít.
Khảo sát sự biến thiên hàm số ,
.
Ta có:
Bảng biến thiên
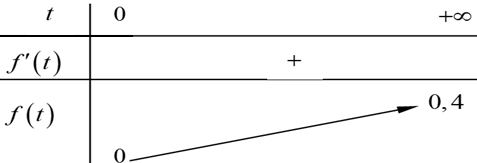
Dựa vào BBT ta thấy giá trị tăng theo
nhưng không vượt ngưỡng
gam/lít.
Vậy .
Mực nước biển trung bình tại trường sa từ năm 2013 đến năm 2019 được cho bởi biểu đồ trong hình bên dưới.
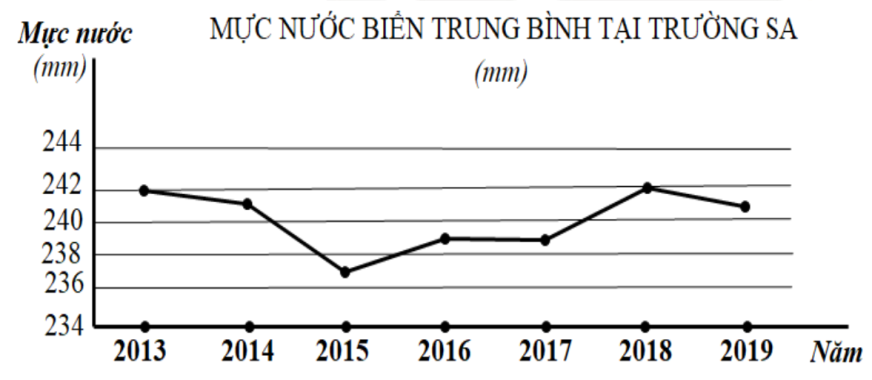
Trong khoảng thời gian từ năm 2016 đến năm 2019, năm nào mực nước biển trung bình tại trường sa cao nhất ?
Nhìn vào biểu đồ ta thấy, tại năm 2018 mực nước biển trung bình tại trường sa cao nhất bằng .
Hình vẽ cho biết nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh đo bằng đơn vị . Hãy cho biết trong năm 2020 tại Thành phố Hồ Chí Minh thì nhiệt độ trung bình của tháng nào cao nhất, nhiệt độ trung bình của tháng nào thấp nhất?
Nhiệt độ trung bình các tháng năm 2020 tại TPHCM
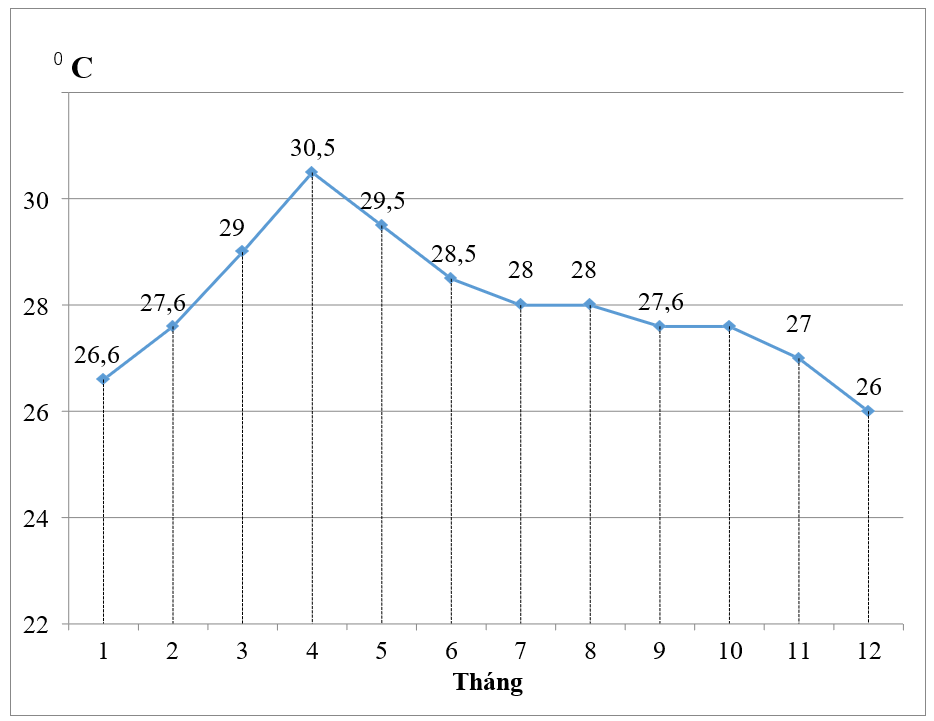
Từ hình vẽ ta thấy nhiệt độ trung bình của tháng cao nhất là tháng 4. Nhiệt độ trung bình của tháng thấp nhất là tháng 12.
Dân số (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức
, trong đó
là thời gian được tính bằng năm. Tìm tốc độ tăng dân số tại thời điểm
.
Tốc độ tăng trưởng dân số là:
Khi thì
Một chất điểm chuyển động của phương trình trong đó
,
tính bằng giây,
tính bằng centimét. Tính vận tốc tức thời của chất điểm tại thời điểm
.
Vận tốc tức thời của chất điểm tại thời điểm là:
.
Vậy vận tốc tức thời của chất điểm tại thời điểm là:
Một chất điểm chuyển động của phương trình trong đó
,
tính bằng giây,
tính bằng mét. Tính vận tốc tức thời của chất điểm tại thời điểm
.
Vận tốc tức thời của chất điểm tại thời điểm là:
.
Vậy vận tốc tức thời của chất điểm tại thời điểm là:
Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán là , trong đó
là giá bán của mỗi sản phẩm mà tại giá bán này có
sản phẩm được bán ra. Khi đó hàm doanh thu của công ty là
Ta có khi có sản phẩm được bán ra thì giá bán là
, do đó doanh thu của cửu hàng khi bán ra
sản phẩm là
.
Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyển động , trong đó
,
là thời gian chuyển động,
là độ cao so với mặt đất. Tính vận tốc tức thời của viên đạn khi viên đạn đạt được độ cao
.
Vận tốc tức thời của viên đạn tại thời điểm là:
Viên đạn đạt được độ caovào thời điểm
kể từ lúc bắn, khi đó vận tốc tức thời của viên đạn là:
.
Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được mét vải lụa
.Tổng chi phí sản xuất
mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 320 nghìn đồng/mét. Gọi là lợi nhuận thu được khi bán
mét vải lụa. Hãy viết biểu thức tính
theo
?
Khi bán mét vải lụa
Số tiền thu được là: .
Lợi nhuận thu được là: .
Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyển động , trong đó
,
là thời gian chuyển động,
là độ cao so với mặt đất. Tại thời điểm viên đạn đạt vận tốc tức thời bằng
thì viên đạn đang ở độ cao bao nhiêu mét so với mặt đất?
Viên đạn đạt vận tốc tức thời bằng ta có phương trình:
Khi đó viên đạn đang ở độ cao là:
.
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao so với bể mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao
của con tàu so với bề mặt của Mặt Trăng được tính (gẩn đúng) bởi hàm
trong đó
là thời gian tính bằng giây và
là độ cao tính bằng kilômét. Gọi
là vận tốc tức thời của con tàu ở thời điểm
(giây) kể từ khi đốt cháy các tên lửa hãm với
. Tại thời điểm
(giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
Vận tốc tức thời của con tàu ở thời điểm ,
, là đạo hàm của hàm số
theo thời gian
. Hàm số
đã cho là:
Để tìm , ta lấy đạo hàm của
:
Vậy hàm số biểu diễn vận tốc tức thời của con tàu ở thời điểm
là:
Để xác định liệu vận tốc của con tàu tại thời điểm t = 25 giây có đang tăng hay giảm, chúng ta cần xem xét đạo hàm bậc hai của hàm số , tức là gia tốc của con tàu.
Gia tốc là đạo hàm của vận tốc
tức là đạo hàm bậc hai của
Tại thời điểm giây, gia tốc của con tàu là:
Vi gia tốc , nên vận tốc của con tàu tại thời điểm
giây đang giảm
Hình bên cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày. Thời điểm nào trong ngày có nhiệt độ thấp nhất ?
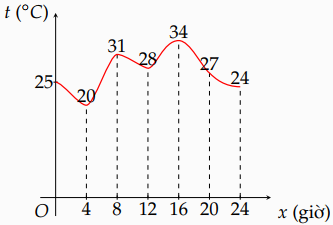
Từ đồ thị ta thấy thời điểm có nhiệt độ thấp nhất trong ngày là vào 4h sáng.
Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất
quả bóng trong một giờ. Chi phí thiết lập các máy này là
nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là
nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động là thấp nhất?
ọi số máy móc công ty sử dụng để sản xuất là .
Thời gian cần để sản xuất hết quả bóng là:
.
Tổng chi phí để sản xuất là:
Ta có: .
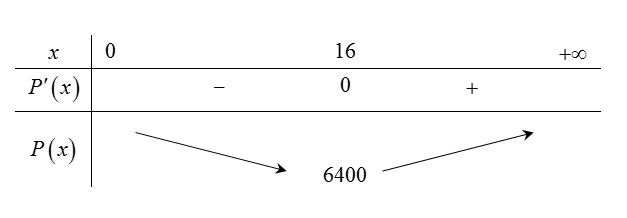
Vậy công ty nên sử dụng máy để chi phí hoạt động là thấp nhất.
Người ta ước tính rằng sau tháng tính từ bây giờ, dân số của một huyện nào đó sẽ là
người. Dân số sẽ thay đổi với tốc độ bao nhiêu sau 12 tháng?
Tốc độ thay đổi dân số tương ứng với thời gian là đạo hàm của hàm dân số. Tức là:
Tốc độ thay đổi:
Tốc độ thay đổi dân số sau 12 tháng sẽ là: người/tháng.
Một cửa hàng bán dầu muốn đóng những thùng đựng dầu có thể tích không đổi bằng , thùng có dạng hình hộp chữ nhật có nắp; đáy là hình vuông cạnh
(
). Trên thị trường, giá nguyên vật liệu làm đáy và nắp thùng là
đồng
, giá nguyên vật liệu làm mặt xung quanh của thùng là
đồng
. Chi phí để cửa hàng làm một thùng đựng dầu được cho bởi công thức?
Hình vẽ minh họa
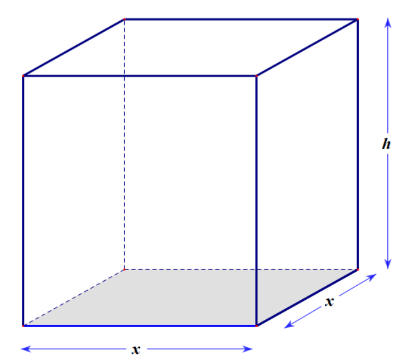
Thể tích của thùng , vì
(
, đơn vị
) là cạnh đáy của thùng nên chiều cao của thùng là:
.
Giá nguyên vật liệu làm đáy và nắp thùng là đồng
, giá nguyên vật liệu làm mặt xung quanh của thùng là
đồng
.
Diện tích mặt đáy, nắp thùng và diện tích xung quanh lần lượt là: . Chi phí làm một thùng đựng dầu là:
.
Trên Mặt Trăng, quãng đường rơi tư do của một vật được cho bởi công thức , với
được tính bằng giây và
tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt Trăng tại thời điểm
.

(Nguồn: https:/www.britannica.complace/Moon)
Vận tốc tức thời của vật là:
Tại thời điểm thì
Giả sử chi phí (USD) để sản xuất
máy vô tuyến là
.
Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ sản phẩm lên
sản phẩm. Giả sử chi phí biên được xác định bởi hàm số
. Hãy tính chi phí sản xuất máy vô tuyến thứ 100.
Chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ sản phẩm lên
sản phẩm. Chi phí biên được xác định bởi hàm số
Chi phí sản xuất 101 máy vô tuyến là:
Chi phí sản xuất 100 máy vô tuyến là:
Chi phí sản xuất máy vô tuyến thứ 100 là
Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là thì độ cao
của nó (tính bằng m) sau
giây được cho bởi công thức
. Tìm vận tốc của vật khi nó chạm đất.
Tại thời điểm mà vật đạt độ cao bằng 0, ta có:
Khi (thời điểm vật chạm đất), ta có:
.
Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động , trong đó
tính bằng giây và
tính bằng centimet. Tìm thời điểm mà vận tốc của con lắc bẳng
.
Ta có:
Vận tốc của con lắc bẳng
=>
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao so với bể mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao
của con tàu so với bề mặt của Mặt Trăng được tính (gẩn đúng) bởi hàm
trong đó
là thời gian tính bằng giây và
là độ cao tính bằng kilômét. Gọi
là vận tốc tức thời của con tàu ở thời điểm
(giây) kể từ khi đốt cháy các tên lửa hãm với
. Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu?
Vận tốc tức thời của con tàu ở thời điểm ,
, là đạo hàm của hàm số
theo thời gian
. Hàm số
đã cho là:
Để tìm , ta lấy đạo hàm của
:
Vậy hàm số biểu diễn vận tốc tức thời của con tàu ở thời điểm
là:
Tại thời điểm bắt đầu hãm phanh , vận tốc của con tàu là:
Một vật rơi tự do có phương trình chuyển động là , trong đó
. Tìm thời điểm mà vận tốc tức thời của vật tại thời điểm đó bằng
.
Thật vậy: .
Ta có: .
Vậy vận tốc tức thời của vật đạt tại thời điểm
.
Giả sử một công ty du lịch bán tour với giá là /khách thì doanh thu sẽ được biểu diễn qua hàm số
. Công ty phải bán giá tour cho một khách là bao nhiêu để doanh thu từ tour xuyên Việt là lớn nhất.
Doanh thu là .
Ta có , tính được
.
Bảng biến thiên
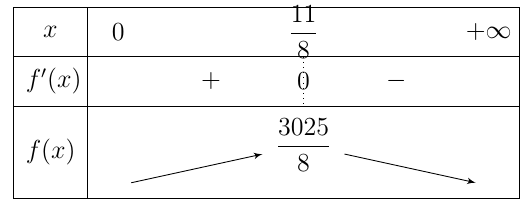
Dựa vào bảng biến thiên ta thấy đạt giá trị lớn nhất khi
Vậy công ty cần bán tour với giá 1,38 triệu đồng/khách thì doanh thu sẽ cao nhất.
Giả sử chi phí (USD) để sản xuất
máy vô tuyến là
.
Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ sản phẩm lên
sản phẩm. Giả sử chi phí biên được xác định bởi hàm số
. Tìm
?
Chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ sản phẩm lên
sản phẩm. Chi phí biên được xác định bởi hàm số
=> Ý nghĩa: Chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 89 sản phẩm lên 90 sản phẩm là 260 (USD)
Một cửa hàng trà sữa có đồ thị biểu diễn số ly trà sữa bán được trong một tuần như sau. Số ly trà sữa cửa hàng đó bán được nhiều nhất trong một ngày là bao nhiêu
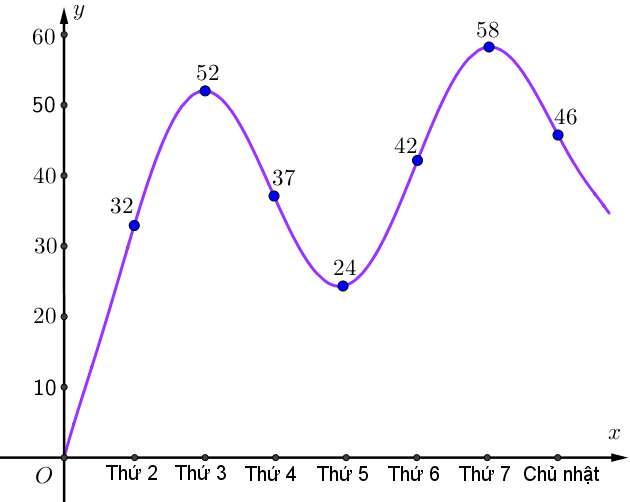
Từ đồ thị ta thấy vào thứ 7 cửa hàng bán được nhiều nhất là 58 ly trà sữa.
Đồ thị bên dưới là tốc độ của một chiếc xe đua trên đoạn đường đua bằng phẳng dài 3 km.
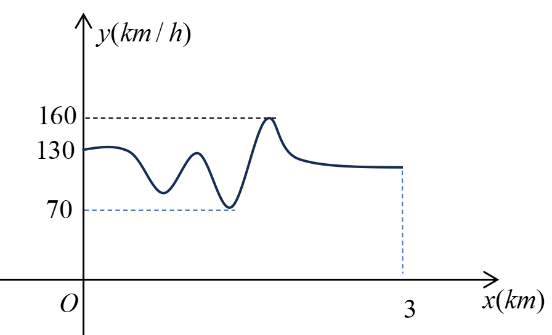
Tốc độ nhỏ nhất của xe đua trên đoạn đường này bằng
Dựa vào đồ thị ta thấy tốc độ nhỏ nhất bằng .
Một công ty chuyên sản xuất thùng phi nhận được đơn đặt hàng với yêu cầu là thùng phi phải có dạng hình trụ và chứa được mỗi chiếc. Hỏi chiếc thùng phải có chiều cao
và bán kính đáy
bằng bao nhiêu để sản xuất ít tốn vật liệu nhất?
Do thùng phi có dạng hình trụ nên:
Diện tích toàn phần của thùng phi là:
Thay vào ta được:
Bảng biến thiên

Vậy để sản xuất thùng phi ít tốn vật liệu nhất thì và chiều cao là
.
Một chủ nhà hàng kinh doanh phần ăn đồng giá có chiến lược kinh doanh như sau:
- Phí cố định được ước tính trong một năm là 50000 nghìn đồng.
- Chi phí một phần ăn ước tính khoảng 22 nghìn đồng.
- Giá niêm yết trên thực đơn là 30 nghìn đồng.
Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu là số phần ăn phục vụ trong một năm, giả sử
thuộc khoảng
a) Gọi lả tổng chi phí hằng năm cho
phần ăn này. Khi đó:
.Sai||Đúng
b) Giá thành của một phần ăn cho bởi biểu thức ( nghìn đồng)Đúng||Sai
c) Dựa vào đồ thị hàm số và đường thẳng y = 30, ta thấy điểm hoà vốn của nhà hàng, tức là số lượng phần ăn tối thiểu phải được phục vụ hằng năm để hoạt động của nhà hàng tạo ra lợi nhuận là 6250. Đúng||Sai
d) Tổng lợi nhuận hằng năm cho phần ăn được biểu thị bởi:
(nghìn đồng).Đúng||Sai
Một chủ nhà hàng kinh doanh phần ăn đồng giá có chiến lược kinh doanh như sau:
- Phí cố định được ước tính trong một năm là 50000 nghìn đồng.
- Chi phí một phần ăn ước tính khoảng 22 nghìn đồng.
- Giá niêm yết trên thực đơn là 30 nghìn đồng.
Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu là số phần ăn phục vụ trong một năm, giả sử
thuộc khoảng
a) Gọi lả tổng chi phí hằng năm cho
phần ăn này. Khi đó:
.Sai||Đúng
b) Giá thành của một phần ăn cho bởi biểu thức ( nghìn đồng)Đúng||Sai
c) Dựa vào đồ thị hàm số và đường thẳng y = 30, ta thấy điểm hoà vốn của nhà hàng, tức là số lượng phần ăn tối thiểu phải được phục vụ hằng năm để hoạt động của nhà hàng tạo ra lợi nhuận là 6250. Đúng||Sai
d) Tổng lợi nhuận hằng năm cho phần ăn được biểu thị bởi:
(nghìn đồng).Đúng||Sai
a)
b) nghìn đồng.
c) Vẽ đồ thị hàm số và đường thẳng
trên cùng một hệ trục tọa độ
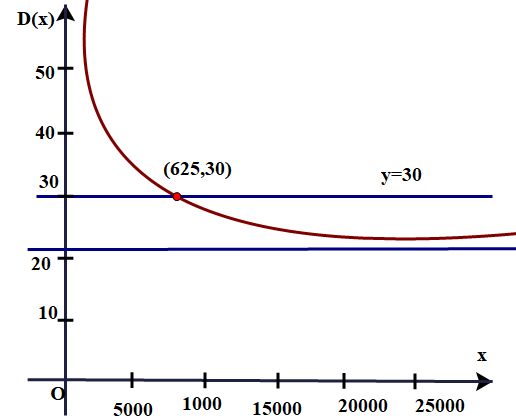
Quan sát đồ thị của hai hàm số, ta thấy giao điểm của đồ thị hàm số và đường thẳng
là điểm có tọa độ
Nghĩa là khi phục vụ được tối thiểu 6250 phần ăn thì chi phí một phần ăn đúng bằng tiền bán một phần ăn (là 30 nghìn đồng).
d) .
Doanh thu (USD) từ việc cho thuê
căn hộ có thể được mô hình hoá bằng hàm số:
Tìm doanh thu biên khi
.
Hàm doanh thu biên là .
Ta có doanh thu biên khi là
.
Kính viễn vọng không gian Hubble được triển khai vào ngày 24 tháng 4 năm 1990, bởi tàu con thoi Discovery. Vận tốc của tàu con thoi trong nhiệm vụ này từ khi xuất phát tại (s) cho đến khi tên lửa đẩy nhiên liệu rắn bị loại bỏ ở
(s) được xác định theo phương trình sau:
(Nguồn: James Stewan, Calculus)
Tính gia tốc tức thời của tàu con thoi trên tại thời điểm (s) (làm tròn kết quả đến hàng phần nghìn).
Gia tốc tức thời của tàu con thoi tại thời điểm (s) là:
Gia tốc tức thời của tàu con thoi tại thời điểm (s) là:
Hình bên cho biết lượng mưa trung bình các tháng năm 2019 tại Thành phố Hồ Chí Minh đo theo đơn vị milimet. Hãy cho biết vào tháng nào trong năm 2019 thì lượng mưa là cao nhất ?
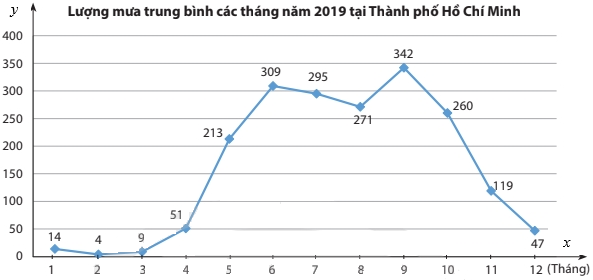
Từ đồ thị ta thấy vào Tháng 9 thì lượng mưa ở Thành phố Hồ Chí Minh cao nhất trong năm 2019
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động , trong đó
tính bằng giây và
tính bằng centimet. Vận tốc tức thời và gia tốc tức thời của con xắc lò xo tại thời điểm
lần lượt là:
Ta có:
a) Vận tốc tức thời của con xắc lò xo tại thời điểm là:
Gia tốc tức thời của con xắc lò xo tại thời điểm là:
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: trong đó
là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
Xét hàm số .
Ta có: .
Khi đó, với .
Bảng biến thiên của hàm số như sau:
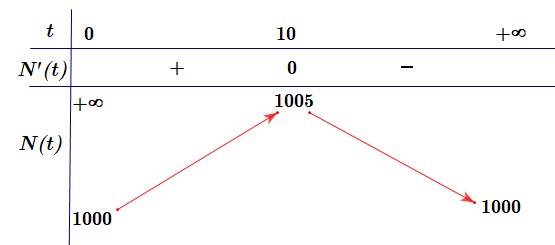
Căn cứ bảng biến thiên, ta thấy: Trên khoảng , hàm số
đạt giá trị lớn nhất bằng 1005 tại
.
Vậy số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng là 1005 con.
Chuyển động của một hạt trên một dây rung được cho bởi công thức , trong đó
tính bằng centimét và
tính bằng giây. Vận tốc của hạt sau
giây là
. Vận tốc cực đại của hạt là bao nhiêu (làm tròn kết quả đến chữ số thập thứ nhất)?
Vận tốc của hạt sau giây là:
.
Vận tốc cực đại của hạt là: , đạt được khi
hay
.
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao so với bể mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao
của con tàu so với bề mặt của Mặt Trăng được tính (gẩn đúng) bởi hàm
trong đó
là thời gian tính bằng giây và
là độ cao tính bằng kilômét. Gọi
là vận tốc tức thời của con tàu ở thời điểm
(giây) kể từ khi đốt cháy các tên lửa hãm với
. Xác định hàm số
.
Vận tốc tức thời của con tàu ở thời điểm ,
, là đạo hàm của hàm số
theo thời gian
. Hàm số
đã cho là:
Để tìm , ta lấy đạo hàm của
:
Vậy hàm số biểu diễn vận tốc tức thời của con tàu ở thời điểm
là:
Chuyển động của một hạt trên một dây rung được cho bởi , trong đó
tính bằng centimét và
tính bằng giây. Tính vận tốc của hạt sau
giây. Vận tốc cực đại của hạt là bao nhiêu?
Đạo hàm của hàm theo thời gian
:
Ta thấy rằng hàm là một hàm cosin với biên độ bằng
, do đó giá trị lớn nhất của hàm này là
.
Vậy vận tốc cực đại của hạt là .
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong giờ được tính theo công thức
. Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
Với ,
ta có
.
Cho
Bảng biến thiên
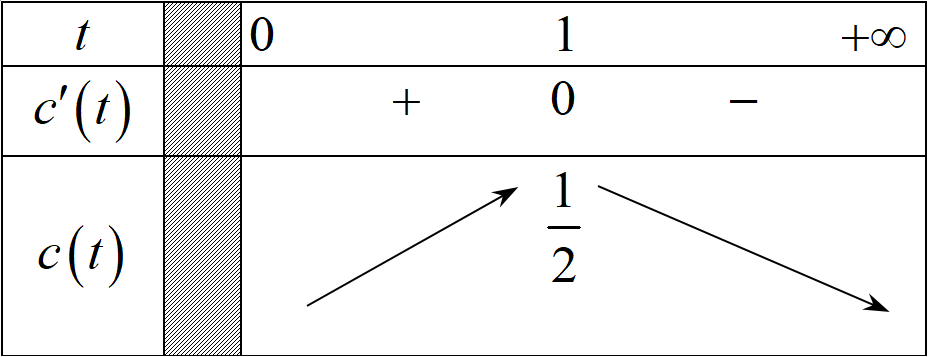
Vậy khi
.
Giả sử chi phí để sản xuất
máy vô tuyến là
.
Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ sản phẩm lên
sản phẩm. Giả sử chi phí biên được xác định bởi hàm số
. Tìm hàm chi phí biên.
Xét là số gia của biến số tại điểm
.
Ta có:
.
Ta thấy: .
Vậy hàm chi phí biên là: .
Một chuyển động thẳng xác định bởi phương trình , trong đó
tính bằng mét và
là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại
.
Vận tốc tức thời của chuyển động là:
Khi
Để điều chỉnh nhiệt độ trong phòng, một hệ thống điều hòa không khí được phép hoạt động trong 10 phút. Gọi là nhiệt độ phòng ở phút thứ
được cho bởi công thức
với
. Trong thời gian
phút kể từ khi hệ thống điều hòa không khí bắt đầu hoạt động, nhiệt độ trong phòng tăng hay giảm?
Xét hàm số với
.
.
Suy ra hàm số nghịch biến trên đoạn
. Vậy trong thời gian
phút kể từ khi hệ thống làm mát bắt đầu hoạt động, nhiệt độ trong phòng giảm.
Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. Khi đó viên đạn cách mặt đất bao nhiêu mét (lấy
)?
Phương trình của viên đạn đi theo phương thẳng đứng được cho bởi:
Vận tốc viên đạn tại thời điểm t là:
Từ đó, ta nhận thấy:
Thời điểm tại đó tốc độ của viên đạn bằng 0 được cho bởi:
Khi đó viên đạn cách mặt đất một khoảng cho bởi:
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất sản phẩm (
) được cho bởi hàm số
và được minh họa bằng đồ thị ở hình bên dưới.
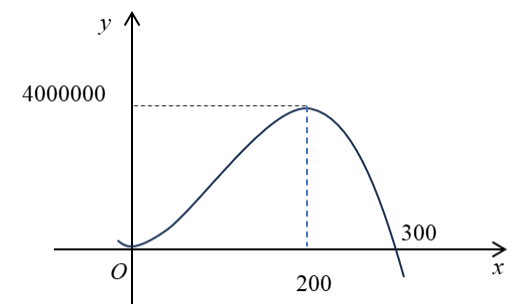
Cần sản xuất bao nhiêu sản phẩm để doanh nghiệp thu được lợi nhuận cao nhất?
Dựa vào đồ thị ta thấy hàm số có giá trị lớn nhất bằng khi
Do đó cần sản suất sản phẩm thì doanh nghiệp thu được lợi nhuận cao nhất.
Số dân của một thị trấn sau năm kể từ đầu năm 2020 được tính bởi công thức
được tính bằng vạn người. Xem
là một hàm số xác định trên nửa khoảng
và đạo hàm của hàm số
biểu thị tốc độ tăng dân số của thị trấn. Trong khoảng thời gian nào dưới đây thì dân số của thị trấn này giảm?
Tốc độ tăng dân số của thị trấn là
Ta cần tìm sao cho
.
Ta có
Kết hợp với điều kiện ta có
.
Do đó dân số của thị trấn giảm trong khoảng thời gian từ đầu năm 2020 đến hết năm 2021.
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ được mô phỏng ở hình. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ
là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số.
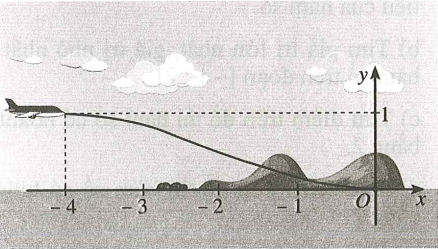
a) Hàm số mô phỏng đường bay của máy bay trên đoạn là hàm số bậc 3 có hệ số a âm. Sai|Đúng
b) Công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn là
. Đúng||Sai
c) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất là dặm? (Biết đơn vị trên hệ trục toạ độ là dặm). Sai|Đúng
d) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang 2 dặm. Đúng||Sai
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ được mô phỏng ở hình. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ
là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số.

a) Hàm số mô phỏng đường bay của máy bay trên đoạn là hàm số bậc 3 có hệ số a âm. Sai|Đúng
b) Công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn là
. Đúng||Sai
c) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất là dặm? (Biết đơn vị trên hệ trục toạ độ là dặm). Sai|Đúng
d) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang 2 dặm. Đúng||Sai
a. Sai
b) .
c) Thay , ta được
.
Vậy khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất (dặm).
d) Thay ta được
. Do
nên
.
Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyển động , trong đó
,
là thời gian chuyển động,
là độ cao so với mặt đất. Sau bao lâu kể từ khi bắn thì viên đạn đạt được độ cao
?
Khi viên đạn đạt được độ cao, ta có phương trình:
Vậy sau kể từ khi bắn thì viên đạn đạt được độ cao
.
Sau khi uống đồ uống có cồn, nồng độ cồn trong máu tăng lên rồi giảm dần được xác định bằng hàm số , trong đó
là nồng độ cồn,
là thời điểm đo tính từ ngay sau khi uống
đồ uống có cồn.
(Nguồn: P. Wilkinson et al., Pharmacokinetics of Ethanol after Ora' Administration in the Fasting State, 1977)
Giả sử một người uống hết nhanh đồ uống có cồn. Tính tốc độ chuyển hoá nồng độ cồn trong máu của người đó tại thời điểm
(h) (làm tròn kết quả đến hàng phần triệu).
Ta có: .
Vậy tốc độ chuyển hoá nồng độ cồn tức thời trong máu của người đó tại thời điểm (h) là:
Một loại vi khuẩn được tiêm một loại thuốc kích thích sự sinh sản. Sau t phút, số vi khuẩn được xác định theo công thức . Hỏi sau bao giây thì số vi khuẩn lớn nhất?
Xét hàm số .
.
.
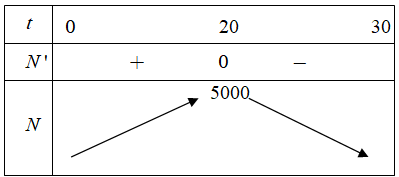
Với giây thì số vi khuẩn lớn nhất.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
