VnDoc.com

Cách dùng Casio giải bài toán tích phân thực tế nhanh và chính xác

Casio tích phân thực tế

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word

Phân loại: Tài liệu Tính phí

Toán 12 tích phân thực tế

A. Mẹo dùng Casio giải nhanh bài toán tích phân thực tế
B. Bài tập tự rèn luyện tính bài toán tích phân thực tế

Trong chương trình Toán THPT, đặc biệt ở lớp 12, các dạng bài toán tích phân thực tế ngày càng xuất hiện nhiều trong các đề kiểm tra và đề thi tốt nghiệp THPT. Các bài toán này thường liên quan đến quãng đường, vận tốc, năng lượng, diện tích, sản lượng,… Yêu cầu học sinh phải biết xử lý số liệu nhanh và chính xác. Vì vậy, việc sử dụng máy tính Casio để hỗ trợ giải phân tích trở thành kỹ năng vô cùng quan trọng, giúp tối ưu thời gian làm bài và hạn chế sai sót.

Bài viết này thuộc chuyên mục Casio tích phân thực tế, sẽ hướng dẫn bạn cách sử dụng máy tính cầm tay Casio để tính phân tích, kiểm tra kết quả, ước lượng và xử lý các bài toán thực tế thường gặp. Mọi thao tác đều được trình bày chi tiết, kèm theo ví dụ minh họa dễ hiểu, giúp học sinh nắm vững phương pháp và áp dụng hiệu quả trong phòng này. Đây là tài liệu hữu ích cho mọi bạn đang luyện thi THPT Quốc Gia hoặc muốn tăng tốc độ làm bài phần tích phân.

A. Mẹo dùng Casio giải nhanh bài toán tích phân thực tế

Bài toán 1. Một người muốn dán tấm bảng hiệu cũ là một phần của hình elip với kích thước như hình vẽ. Tính gần đúng chi phí mà người đó phải bỏ ra để mua giấy dán biết giá của $1m^{2}$ $1m^{2}$ giấy là $20000$ ?

Hướng dẫn giải:

Xây dựng hệ trục tọa độ $Oxy$ như hình:

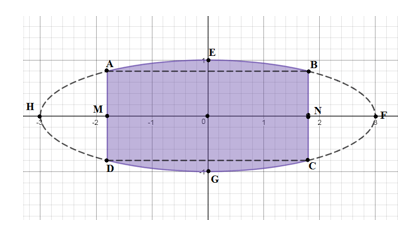
Phương trình Elip có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(E)$

($a,b$ lần lượt là nữa trục dài và trục ngắn của Elip)

Theo đề bài ta có: $b = OE = \frac{1}{2}EG = 1$ $b = OE = \frac{1}{2}EG = 1$

Do $B(1.8;0.8) \in (E)$ $B(1.8;0.8) \in (E)$ nên $\frac{1.8^{2}}{a^{2}} + \frac{0.8^{2}}{1^{2}} = 1 \Rightarrow a^{2} = 9$ $\frac{1.8^{2}}{a^{2}} + \frac{0.8^{2}}{1^{2}} = 1 \Rightarrow a^{2} = 9$

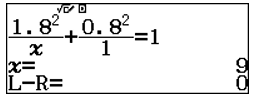
Suy ra $(E):\frac{x^{2}}{9} + y^{2} = 1$ $(E):\frac{x^{2}}{9} + y^{2} = 1$ hay $y = \pm \sqrt{1 - \frac{x^{2}}{9}}$ $y = \pm \sqrt{1 - \frac{x^{2}}{9}}$

Ta có: $S = 4S_{OEBN} = 4\int_{0}^{1.8}{\sqrt{1 - \frac{x^{2}}{9}}dx}$ $S = 4S_{OEBN} = 4\int_{0}^{1.8}{\sqrt{1 - \frac{x^{2}}{9}}dx}$

Sử dụng máy tính CASIO fx- 580VN X tính tích phân trên và lưu vào A

Vậy số tiền người chủ phải bỏ ra để mua giấy dán là

$20000A \approx 134820$ $20000A \approx 134820$

Nhận xét:

Đối với những bài toán tính diện tích của một hình phức tạp không có sẵn công thức ta có thể sử dụng tích phân để tính diện tích
Để có thể áp dụng tích phân để tính diện tích ta cần xây dựng hệ trục tọa độ $Oxy$ và xây dựng các hàm số phù hợp, đơn giản mà không mất tính tổng quát, kết quả diện tích không sai lệch.

Bài toán 2. Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian quy luật $v(t) = \frac{1}{120}t^{2} + \frac{58}{45}t(m/s)$ $v(t) = \frac{1}{120}t^{2} + \frac{58}{45}t(m/s)$ trong đó $t$ (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 3 giây so với và có gia tốc bằng $a(m/s^{2})$ $a(m/s^{2})$ ($a$ là hằng số). Sau khi B xuất phát được $15s$ thì đuổi kịp A. Vận tốc B tại thời điểm đuổi kịp A bằng

A. $25(m/s)$ B. $30(m/s)$ C.$36(m/s)$ D.$21(m/s)$

Hướng dẫn giải

Tính quãng đường A đi được cho đến khi B đuổi kịp A

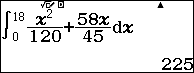
$S = \int_{0}^{18}{v_{A}(t)dt} = \int_{0}^{18}{\left( \frac{1}{120}t^{2} + \frac{58}{45}t \right)dt} = 225$ $S = \int_{0}^{18}{v_{A}(t)dt} = \int_{0}^{18}{\left( \frac{1}{120}t^{2} + \frac{58}{45}t \right)dt} = 225$

Tính quãng đường B đi được cho đến khi B đuổi kịp A

Vận tốc của B tại thời điểm $t(s)$ tính từ lúc B xuất phát là $v_{B}(t) = at(m/s)$ $v_{B}(t) = at(m/s)$

Quãng đường B đi được cho đến khi B đuổi kịp A

$S = \int_{0}^{15}{v_{B}(t)dt = \int_{0}^{15}{at}}dt = \frac{at^{2}}{2}\left| \begin{matrix} 15 \\ 0 \\ \end{matrix} \right.\ = \frac{225}{2}a(m)$ $S = \int_{0}^{15}{v_{B}(t)dt = \int_{0}^{15}{at}}dt = \frac{at^{2}}{2}\left| \begin{matrix} 15 \\ 0 \\ \end{matrix} \right.\ = \frac{225}{2}a(m)$

Tính vận tốc B tại thời điểm đuổi kịp A: $\frac{225}{2}a = 225 \Leftrightarrow a = 2$ $\frac{225}{2}a = 225 \Leftrightarrow a = 2$

$v_{B}(t) = 2t \Rightarrow v_{B}(15) = 30(m/s)$ $v_{B}(t) = 2t \Rightarrow v_{B}(15) = 30(m/s)$

Đáp án B

Lưu ý: Để có thể làm tốt các bài toán trên, chúng ta cần nhớ mối hệ của các đại lượng Quãng đường $S(t)$ , Vận tốc $v(t)$ và Gia tốc $a(t)$

Quãng đường đi được $S(t)$là nguyên hàm của vận tốc $v(t)$
Quãng đường đi được của vật trong khoảng thời gian nào bằng tích phân của hàm vận tốc $v(t)$ khi biến $t$ chạy trong khoảng thời gian đó.
Đạo hàm của vận tốc $v(t)$ tại thời điểm $t$ chính là gia tốc của vật chuyển động tại thời điểm đó $a(t)$ .

Bài toán 3. Người ta thay nước mới cho 1 bể bơi có dạng hình hộp chữ nhật có độ sâu là $h_{1} = 300cm$ $h_{1} = 300cm$. Giả sử $h(t)$ là chiều cao (tính bằng cm) của mực nước bơm được tại thời điểm $t$ giây, biết rằng tốc độ tăng chiều cao mực nước tại giây thứ $t$ là $h'(t) = \frac{1}{500}\sqrt[3]{t + 3}$ và lúc đầu hồ bơi không có nước. Hỏi sau bao lâu thì nước bơm được $\frac{3}{4}$ $\frac{3}{4}$ độ sâu của hồ bơi

2 giờ 7 phút
1 giờ 7 phút
4 giờ 7 phút
3 giờ 7 phút

Hướng dẫn giải

Mực nước của hồ bơi tại thời gian $t$ giây là: $h(t) = h(0) + \int_{0}^{t}{\left( \frac{1}{500}\sqrt[3]{x + 3} \right)dx} = \int_{0}^{t}{\left( \frac{1}{500}\sqrt[3]{x + 3} \right)dx}$ $h(t) = h(0) + \int_{0}^{t}{\left( \frac{1}{500}\sqrt[3]{x + 3} \right)dx} = \int_{0}^{t}{\left( \frac{1}{500}\sqrt[3]{x + 3} \right)dx}$

Theo đề bài, lượng nước bơm được bằng $\frac{3}{4}$ $\frac{3}{4}$ độ sâu của hồ bơi nên ta có:

$h(t) = \frac{3}{4}h_{1} \Leftrightarrow \int_{0}^{t}{\left( \frac{1}{500}\sqrt[3]{x + 3} \right)dx} = \frac{3}{4}300 = 225$ $h(t) = \frac{3}{4}h_{1} \Leftrightarrow \int_{0}^{t}{\left( \frac{1}{500}\sqrt[3]{x + 3} \right)dx} = \frac{3}{4}300 = 225$

Dùng chức năng SOLVE của Casio fx 580vnx để tìm nghiệm cho phương trình trên:

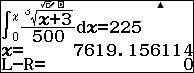
Vậy $t \approx 7619 \approx$ $t \approx 7619 \approx$2 giờ 7 phút

Đáp án A

Bài toán 4. Ban đầu trong một mẫu nước có khoảng $600$con vi khuẩn, trong 1 giờ số lượng này tăng lên với tốc độ $v(t) = 400e^{1.25t}$ $v(t) = 400e^{1.25t}$. Hỏi sau 3 giờ, 5giờ và 7 giờ số lượng vi khuẩn trong mẫu lần lượt là bao nhiêu?

$13886 - 166044 - 2019700$
$17608 - 207805 - 2524875$
$18808 - 210205 - 2528475$
$18702 - 220350 - 2516969$

Hướng dẫn giải

Cách 1: Đặt $S(t)$ là số vi khuẩn trong mẫu sau $t$ giờ

Khi đó ta có: $S(t) = \int_{}^{}{v(t)dt = \int_{}^{}{400e^{1.25t}dt = 320e^{1.25t} + C}}$ $S(t) = \int_{}^{}{v(t)dt = \int_{}^{}{400e^{1.25t}dt = 320e^{1.25t} + C}}$

Theo đề bài ta có: $S(0) = 600 \Leftrightarrow 320 + C = 600 \Leftrightarrow C = 280$ $S(0) = 600 \Leftrightarrow 320 + C = 600 \Leftrightarrow C = 280$

Suy ra: $S(t) = 320e^{1.25t} + 280$ $S(t) = 320e^{1.25t} + 280$

Sử dụng Casio fx 580vnx tìm số lượng vi khuẩn sau 3 giờ, 5giờ và 7 giờ

Nhập biểu thức vào máy:

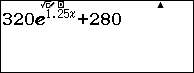
Sử dụng lệnh r lần lượt tại các giá trị $x = 3$; $x = 5$ và $x = 7$

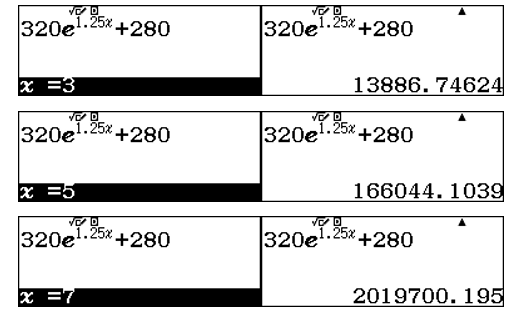
Đáp án A

Cách 2 Đặt $S(t)$ là số vi khuẩn trong mẫu sau $t$ giờ

Ta có $S(t) = S(0) + \int_{0}^{t}{400e^{1.25x}dx = 600 +}\int_{0}^{t}{400e^{1.25x}dx}$ $S(t) = S(0) + \int_{0}^{t}{400e^{1.25x}dx = 600 +}\int_{0}^{t}{400e^{1.25x}dx}$

Nhập biểu thức vào máy:

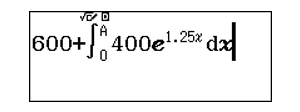
Sử dụng lệnh r lần lượt tại các giá trị $A = 3$; $A = 5$ và $A = 7$

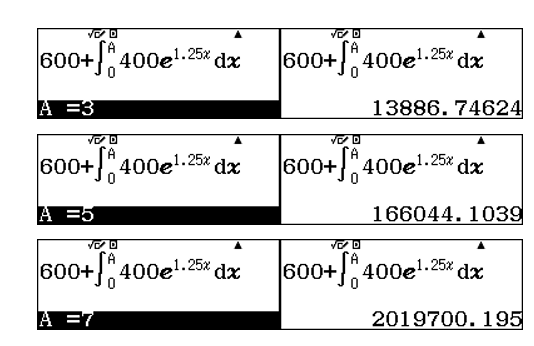
Đáp án A

B. Bài tập tự rèn luyện tính bài toán tích phân thực tế

Bài toán 1 Một xe ô tô đang chạy thì phanh lại. Sau khi đạp phanh, ô tô bắt đầu chuyển động chậm dần đều với vận tốc $v(t) = - 40t + 20(m/s)$, trong đó $t$ là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ?

A. $4.5(m)$ B. $5(m)$ C.$5.5(m)$ D.$6(m)$

Bài toán 2. Một công ty dự định đầu tư một khu nhà máy sản xuất. Giả sử sau $t$ năm, dự án lần 1 có tốc độ phát sinh lợi nhuận là $P_{1}(t) = 100 + t^{2}$ $P_{1}(t) = 100 + t^{2}$trăm đôla/năm, tiếp sau đó dự án lần 2 có tốc độ phát sinh lợi nhuận là $P_{2}(t) = 150 + 5t$ $P_{2}(t) = 150 + 5t$ trăm đôla/năm. Biết rằng sau thời gian $t$ thì tốc độ lợi nhuận lần 1 gấp 2 lần tốc độ lợi nhuận lần 2. Tính lợi nhuận chênh lệch thực tế cho khoảng thời gian trên

$676.66$ trăm đô
$755$ trăm đô
$750$ trăm đô
$666.67$ trăm đô

Bài toán 3. Công ty vừa đưa vào một dây chuyền sản xuất để chế tạo máy tính mới. Sau vài tuần, sản lượng đạt được $q(t) = 2000\left\lbrack 1 - \frac{10}{(10 - t)^{2}} \right\rbrack$ $q(t) = 2000\left\lbrack 1 - \frac{10}{(10 - t)^{2}} \right\rbrack$ máy/tuần. Tìm số máy sản xuất được từ đầu tuần thứ ba đến hết tuần thứ tư

$147$ máy
$1523$ máy
$1470$ máy
$3166$ máy

Bài toán 4. Một cái lu có bán kính ở 2 đầu là$2(dm)$và ở giữa là $4(dm)$, chiều cao của cái lu là $8(dm)$. Tính lượng nước tối đa mà lu có thể chứa được.

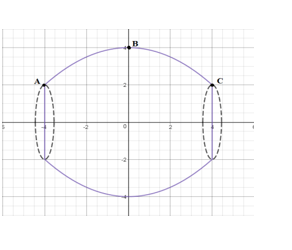
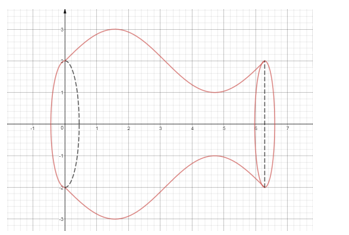
Bài toán 5: Tính thể tích cái bình hoa với kích thước như hình vẽ biết bình cao $2\pi(cm)$ $2\pi(cm)$ và đường sinh của bình khi nằm ngang là đường cong có dạng $y = sinx + 2$?

Bài toán 6: Vận tốc chuyển động của máy bay là $v(t) = 6t^{2} + 1(m/s)$ $v(t) = 6t^{2} + 1(m/s)$. Hỏi quãng đường máy bay bay từ giây thứ 5 đến giây thứ 15 là bao nhiêu?

A. $2400m$ B. $1202m$ C. $6510m$ D. $1134m$.

C. Đáp án bài tập tự rèn luyện tính tích phân thực tế

Bài 1:

Chọn mốc thời gian là lúc người lái xe đạp phanh và $T$ là thời điểm ô tô dừng hẳn

Khi đó $v(T) = 0$ hay $- 40T + 20 = 0$. Suy ra $T = 0.5$

Như vậy, kể từ lúc đạp phanh ô tô mất thêm $0.5s$ để dừng hẳn và quãng đường ô tô di chuyển trong thời gian này là: $S = \int_{0}^{0.5}{v(t)dt =}\int_{0}^{0.5}{( - 40t + 20)dt}$ $S = \int_{0}^{0.5}{v(t)dt =}\int_{0}^{0.5}{( - 40t + 20)dt}$

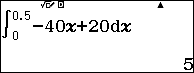
Đáp án: B

Bài 2

Khoảng thời gian $t(t > 0)$ để tốc độ lợi nhuận lần 1 gấp 2 lần tốc độ lợi nhuận lần 2 là nghiệm dương của phương trình:

$P_{1}(t) = 2P_{2}(t)$ $P_{1}(t) = 2P_{2}(t)$

$\Leftrightarrow 100 + t^{2} = 300 + 10t \Leftrightarrow \left\lbrack \begin{matrix} t = 20 \\ t = - 10 \end{matrix} \right.$ $\Leftrightarrow 100 + t^{2} = 300 + 10t \Leftrightarrow \left\lbrack \begin{matrix} t = 20 \\ t = - 10 \end{matrix} \right.$

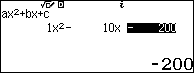
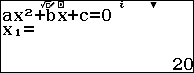
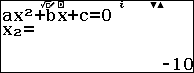
Vậy lợi nhuận chênh lệch thực tế cho khoảng thời gian $0 \leq t \leq 20$ $0 \leq t \leq 20$ là

$\int_{0}^{20}\left\lbrack P_{1}(t) - P_{2}(t) \right\rbrack dt = \int_{0}^{20}{\left\lbrack \left( 100 + t^{2} \right) - (150 + 5t) \right\rbrack dt = \int_{0}^{20}{\left( t^{2} - 5t - 50 \right)dt}}$ $\int_{0}^{20}\left\lbrack P_{1}(t) - P_{2}(t) \right\rbrack dt = \int_{0}^{20}{\left\lbrack \left( 100 + t^{2} \right) - (150 + 5t) \right\rbrack dt = \int_{0}^{20}{\left( t^{2} - 5t - 50 \right)dt}}$

Đáp án D

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-------------------------------------

Hy vọng rằng qua bài viết, bạn đã biết cách sử dụng phân tích toán học Casio nhanh chóng và chính xác , từ thao tác biểu thức, sử dụng phân tích chức năng, kiểm tra kết quả để xử lý các loại bài nâng cao. Khi luyện tập thường xuyên, bạn sẽ tối ưu hóa thời gian làm bài, giảm thiểu sai số và tự động hoàn thành mọi dạng bài tích trong các kỳ quan trọng.

Đừng quên lưu lại bài viết và tiếp tục khám phá thêm nhiều nội dung trong chuyên môn Casio tích phân thực tế như kiểm tra cách tra đạo hàm bằng Casio, tìm phương pháp xử lý, xử lý bảng số liệu thực tế,… Tất cả đều được biên dịch rõ ràng, chính xác và tham gia chương trình Toán 12, phù hợp cho sinh viên muốn nâng cao hiệu quả học tập. Nếu bạn muốn tổng hợp thêm bài phân tích, tạo tập tin PDF công thức Casio, hoặc viết bộ chủ đề Casio giải toán 12, hãy yêu cầu lại — mình luôn sẵn sàng hỗ trợ bạn đầy đủ nhất!

Tải về

Chọn file muốn tải về: