Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập Toán 12 Tính góc trong không gian

Ôn thi THPT Quốc gia Môn Toán

Tính góc trong không gian là một chuyên đề quan trọng trong chương trình Toán 12 phần hình học không gian. Đây là dạng bài thường xuyên xuất hiện trong các đề kiểm tra và đề thi THPT Quốc gia. Bài viết này sẽ giúp bạn hệ thống hóa kiến thức lý thuyết, công thức tính góc giữa đường thẳng và mặt phẳng, góc giữa hai đường thẳng, góc giữa hai mặt phẳng,... cùng với các bài tập minh họa có lời giải chi tiết. Thông qua việc luyện tập và phân tích từng dạng bài, bạn sẽ nắm vững phương pháp giải và nâng cao kỹ năng xử lý bài toán hình học không gian một cách hiệu quả nhất. Hãy cùng khám phá và luyện tập ngay dưới đây để đạt điểm cao trong kỳ thi sắp tới!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 31 câu
  • Điểm số bài kiểm tra: 31 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Chọn đáp án chính xác

    Trong không gian với hệ trục toạ độ Oxyz cho mặt phẳng \left( P \right):x + y - z + 2 = 0 và hai đường thẳng d:\left\{ \begin{matrix} x = 1 + t \\ y = t \\ z = 2 + 2t \\ \end{matrix} \right.\ ;d':\left\{ \begin{matrix} x = 3 - t' \\ y = 1 + t' \\ z = 1 - 2t' \\ \end{matrix} \right.. Biết rằng có 2 đường thẳng có các đặc điểm: song song với (P); cắt d;d' và tạo với d góc 30^{0}. Tính cosin góc tạo bởi hai đường thẳng đó.

    Hướng dẫn:

    Gọi \Delta là đường thẳng cần tìm, \overrightarrow{n_{(P)}} là VTPT của mặt phẳng (P).

    Gọi M(1 + t;t;2 + 2t) là giao điểm của \Delta và d;M'(3 - t';1 + t';;1 - 2t') là giao điểm của \Delta và d’

    Ta có: \overrightarrow{MM'} = (2 - t' - t;t' - t; - 1 - 2t' - 2t)

    MM'//(P) \Leftrightarrow \left\{ \begin{matrix} M \in (P) \\ \overrightarrow{MM'}\bot\overrightarrow{n_{(P)}} \\ \end{matrix} \right.

    \Rightarrow t' = - 2 \Rightarrow \overrightarrow{MM'} = (4 - t; - 1 - t;3 - 2t)

    Ta có: cos30^{0} = \cos\left( \overrightarrow{MM'};\overrightarrow{u_{d}} \right)

    \Leftrightarrow \frac{\sqrt{3}}{2} = \frac{| - 6t + 9|}{\sqrt{36t^{2} - 108t + 156}}

    \Leftrightarrow \left\lbrack \begin{matrix} t = 4 \\ t = - 1 \\ \end{matrix} \right.

    Vậy, có 2 đường thằng thoả mãn là \Delta_{1}:\left\{ \begin{matrix} x = 5 \\ y = 4 + t \\ \end{matrix} \right.\ ;\Delta_{2}:\left\{ \begin{matrix} x = t \\ y = - 1 \\ z = 10 + t \\ \end{matrix} \right.

    Khi đó, \cos\left( \Delta_{1};\Delta_{2} \right) = \frac{1}{2}

  • Câu 2: Thông hiểu
    Tính giá trị biểu thức

    Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d_{1}:\frac{x - 1}{2} = \frac{y - 2}{- 2} = \frac{z + 1}{- 1} và d_{2}:\left\{ \begin{matrix} x = t \\ y = 0 \\ z = - t \\ \end{matrix} \right.. Mặt phẳng (P) qua d_{1} tạo với d_{2} một góc 45^{0} và nhận vectơ \overrightarrow{n} = (1;b;c) làm một vectơ pháp tuyến. Xác định tích bc.

    Hướng dẫn:

    Đường thẳng d_{1};d_{2} có vectơ chỉ phương lần lượt là \overrightarrow{u_{1}} = (2; - 2; - 1) và \overrightarrow{u_{2}} = (1;0; - 1).

    Mặt phẳng (P) có vectơ pháp tuyến là \overrightarrow{n} = (1;b;c).

    \left\{ \begin{matrix} \overrightarrow{n}.\overrightarrow{u_{1}} = 0 \\ \cos\left( \overrightarrow{n};\overrightarrow{u_{2}} \right) = \sin\left( d_{2};(P) \right) \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} 2.1 + ( - 2).b + ( - 1).c = 0 \\ \frac{\left| 1.1 + 0.b + ( - 1).c \right|}{\sqrt{1 + b^{2} + c^{2}}.\sqrt{2}} = \frac{1}{\sqrt{2}} \\ \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} 2 - 2b - c = 0 \\ |1 - c| = \sqrt{1 + b^{2} + c^{2}} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} 2b + c = 2 \\ (1 - c)^{2} = 1 + b^{2} + c^{2} \\ \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} 2b + c = 2 \\ b^{2} + 2c = 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} b = 2 \\ c = - 2 \\ \end{matrix} \right.

    Vậybc = - 4.

  • Câu 3: Thông hiểu
    Xác định tổng tất cả các giá trị tham số m

    Trong không gian Oxyz, cho mặt cầu (S):(x - 1)^{2} + y^{2} + (z + 2)^{2} = 4 và đường thẳng d:\left\{ \begin{matrix} x = 2 - t \\ y = t \\ z = m - 1 - t \\ \end{matrix} \right. Tổng các giá trị thực của tham số m để d cắt (S) tại hai điểm phân biệt A; B và các tiếp diện của (S) tại A; B tạo với nhau một góc lớn nhất bằng

    Hướng dẫn:

    Mặt cầu (S) có tâm I(1;0; - 2) và bán kính R = 2.

    Các tiếp diện của (S) tại A và B tạo với nhau một góc lớn nhất

    ( bằng 90^{0})

    \Leftrightarrow IA\bot IB \Leftrightarrow d(I;d) = \frac{R}{\sqrt{2}} = \sqrt{2}

    Đường thẳng d đi qua điểm M(2;0;m - 1) và có một VTCP \overrightarrow{u} = ( - 1;1; - 1).

    Suy ra: \overrightarrow{IM} = (1;0;m + 1), \left\lbrack \overrightarrow{IM},\overrightarrow{u} \right\rbrack = ( - m - 1; - m;1).

    d(I;d) = \sqrt{2} \Leftrightarrow \frac{\left| \left\lbrack \overrightarrow{IM},\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \sqrt{2}

    \Leftrightarrow \frac{\sqrt{2m^{2} + 2m + 2}}{\sqrt{3}} = \sqrt{2}

    \Leftrightarrow m^{2} + m - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = 2 \\ m = - 2 \\ \end{matrix} \right.

    Vậy tổng các giá trị thực của tham số m bằng -1.

  • Câu 4: Thông hiểu
    Xác định góc giữa hai đường thẳng

    Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳngd_{1}:\left\{ \begin{matrix} x = - t \\ y = - 1 + 4t \\ z = 3t \\ \end{matrix} \right. và d_{2}:\frac{x}{1} = \frac{y + 8}{- 4} = \frac{z + 3}{- 3}. Xác định góc giữa hai đường thẳng d_{1} và d_{2}.

    Hướng dẫn:

    Đường thẳng d_{1} có VTCP\overrightarrow{u_{1}} = ( - 1;4;3), d_{2} có VTCP \overrightarrow{u_{2}} = (1; - 4; - 3) = - \overrightarrow{u_{1}}.

    Vậy góc giữa hai đường thẳng là 0^{0}

  • Câu 5: Nhận biết
    Chọn đáp án thích hợp

    Trong không gianOxyz, cho hai đường thẳng \Delta_{1}:\frac{x - 1}{2} = \frac{y - 2}{- 3} = \frac{z - 3}{1} và\Delta_{2}:\frac{x + 3}{3} = \frac{y - 2}{1} = \frac{z + 1}{- 2}. Tính cosin góc giữa hai đường thẳng \Delta_{1};\Delta_{2}?

    Hướng dẫn:

    Véc tơ chỉ phương của \Delta_{1} là \overrightarrow{u_{1}} = (2; - 3;1)

    Véc tơ chỉ phương của \Delta_{2} là \overrightarrow{u_{2}} = (3;1; - 2)

    \cos\left( \Delta_{1};\Delta_{2} \right) = \cos\left( \overrightarrow{u_{1}};\overrightarrow{u_{2}} \right) = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right|}{\left| \overrightarrow{u_{1}} \right|\left| \overrightarrow{u_{2}} \right|} = \frac{1}{14}.

  • Câu 6: Nhận biết
    Tìm góc giữa hai đường thẳng

    Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng

    \Delta:\left\{ \begin{matrix} x = t \\ y = 5 - 2t \\ z = 14 - 3t \\ \end{matrix} \right. và \Delta':\left\{ \begin{matrix} x = 1 - 4t \\ y = 2 + t \\ z = - 1 + 5t \\ \end{matrix} \right.. Xác định góc giữa hai đường thẳng \Delta và \Delta'.

    Hướng dẫn:

    Đường thẳng \Delta có VTCP \overrightarrow{u} = (1; - 2; - 3), \Delta' có VTCP \overrightarrow{u'} = ( - 4;1;5).

    Gọi \varphi là góc giữa hai đường thẳng \Delta và \Delta'.

    Ta có \cos\varphi = \left| \cos\left( \overrightarrow{u},\overrightarrow{u'} \right) \right|

    = \frac{\left| 1.( - 4) + ( - 2).1 + ( - 3).5 \right|}{\sqrt{1^{2} + ( - 2)^{2} + ( - 3)^{2}}.\sqrt{( - 4)^{2} + 1^{2} + 5^{2}}} = \frac{\sqrt{3}}{2}

    \rightarrow \varphi = 30^{0}.

  • Câu 7: Vận dụng
    Tính giá trị của biểu thức

    Trong không gian Oxyz, cho đường thẳng \Delta:\left\{ \begin{matrix} x = 1 + 2t \\ y = 2 + t \\ z = - 2 - t \end{matrix} \right.và (P): - x + 2y + 2z + 5 = 0. Gọi d là đường thẳng đi qua điểm A( - 1;0; - 1) cắt đường thẳng \Delta_{1} và tạo với đường thẳng \Delta_{2} một góc nhỏ nhất. Vectơ chỉ phương \overrightarrow{u_{d}} = (a;b;c). Tính tổng a + 2b - 3c?

    Hướng dẫn:

    Giả sử đường thẳng dcắt đường thẳng \Delta_{1} tại B, ta có: B(1 + 2t;2 + t; - 2 - t) \in \Delta_{1}.

    Đường thẳng dcó VTCP là: \overrightarrow{AB} = (2t + 2;t + 2; - t - 1), mặt phẳng (P) có VTPT \overrightarrow{n} = ( - 1;2;2).

    Gọi \varphi là góc giữa d và \Delta_{2}, ta có:

    \sin\varphi = \frac{| - 2t - 2 + 2t + 4 - 2t - 2|}{3\sqrt{6t^{2} + 14t + 9}} = \frac{|2t|}{3\sqrt{6t^{2} + 14t + 9}} \geq 0

    \Rightarrow d tạo với đường thẳng \Delta_{2} một góc \varphi nhỏ nhất khi \varphi = 0{^\circ}hay \sin\varphi = 0 \Rightarrow t = 0.

    Khi đó đường thẳng d đi qua điểm A( - 1;0; - 1) và có VTCP \overrightarrow{AB} = (2;2; - 1).

    Vậy a = 2,b = 2,c = - 1

    \Rightarrow a + 2b - 3c = 2 + 2.2 - 3.( - 1) = 9

  • Câu 8: Thông hiểu
    Tính góc giữa hai cạnh

    Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1) và D( - 2;1; - 1). Góc giữa hai cạnh AB và CD có số đo là:

    Hướng dẫn:

    Ta có \overrightarrow{AB} = ( - 1;1;0) và \overrightarrow{CD} = ( - 2;1; - 2).

    Gọi \varphi là góc giữa hai đường thẳng AB và CD.

    Ta có \cos\varphi = \left| \cos\left( \overrightarrow{AB},\overrightarrow{CD} \right) \right| = \frac{\sqrt{2}}{2} \rightarrow \varphi = 45^{0}.

  • Câu 9: Nhận biết
    Tính góc giữa hai đường thẳng

    Tính góc của hai đường thẳng (D):\frac{x - 1}{2} = \frac{y + 3}{4} = \frac{z + 2}{4} và

    (d):x = 3 + 2t;y = 2t - 4; z = 2 \left( t\mathbb{\in R} \right).

    Hướng dẫn:

    (D) và (d) có vectơ chỉ phương \overrightarrow{a} = (2,4,4);\overrightarrow{b} = (2,2,0)

    \Rightarrow \cos\alpha = \frac{|2.2 + 4.2 + 4.0|}{6.2\sqrt{2}} = \frac{\sqrt{2}}{2} \Rightarrow \alpha = 45^{0}

  • Câu 10: Thông hiểu
    Tính góc giữa đường thẳng và mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:\frac{x - 3}{2} = \frac{y - 2}{1} = \frac{z}{1} và mặt phẳng (\alpha):3x + 4y + 5z + 8 = 0. Góc giữa đường thẳng (d) và mặt phẳng (d) có số đo là:

    Hướng dẫn:

    Đường thẳng d có VTCP \overrightarrow{u_{d}} = (2;1;1). Mặt phẳng (\alpha) có VTPT \overrightarrow{n_{\alpha}} = (3;4;5).

    Gọi \varphi là góc giữa đường thẳng d và mặt phẳng (\alpha).

    Ta có \sin\varphi = \left| \cos\left( \overrightarrow{n_{\alpha}};\overrightarrow{u_{d}} \right) \right| = \frac{\sqrt{3}}{2} \Rightarrow \varphi = 60^{0}

  • Câu 11: Nhận biết
    Tính góc giữa hai đường thẳng

    Trong không gian với hệ tọa độ Oxyz, tính góc giữa hai đường thẳng d_{1}:\frac{x}{1} = \frac{y + 1}{- 1} = \frac{z - 1}{2} và d_{2}:\frac{x + 1}{- 1} = \frac{y}{1} = \frac{z - 3}{1}.

    Hướng dẫn:

    Ta có:

    \cos\left( \widehat{d_{1};d_{2}} \right) = \left| \cos\left( \overrightarrow{n_{d_{1}}};\overrightarrow{n_{d_{2}}} \right) \right|

    = \frac{\left| 1.( - 1) + ( - 1).1 + 2.1 \right|}{\sqrt{1^{2} + ( - 1)^{2} + 2^{2}}\sqrt{( - 1)^{2} + 1^{2} + 1^{2}}} = 0

    \Rightarrow \left( \widehat{d_{1};d_{2}} \right) = 90{^\circ}

  • Câu 12: Thông hiểu
    Tính góc giữa đường thẳng và mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:\left\{ \begin{matrix} x = 6 + 5t \\ y = 2 + t \\ z = 1 \\ \end{matrix} \right. và mặt phẳng 3x-2y=0. Tính góc hợp bởi giữa đường thẳng d và mặt phẳng (P).

    Hướng dẫn:

    Đường thẳng d có VTCP \overrightarrow{u_{d}} = (5;1;0).

    Mặt phẳng (P) có VTPT \overrightarrow{n_{(P)}} = (3; - 2;0).

    Gọi \varphi là góc giữa đường thẳng d và mặt phẳng (P).

    Ta có \sin\varphi = \left| \cos\left( \overrightarrow{u_{d}};\overrightarrow{n_{(P)}} \right) \right| = \frac{\sqrt{2}}{2} \Rightarrow \varphi = 45^{0}

  • Câu 13: Vận dụng
    Chọn đáp án đúng

    Trong không gian Oxyz, cho mặt phẳng (P):ax + by + cz - 1 = 0với c < 0 đi qua 2 điểm A(0;1;0);B(1;0;0) và tạo với (Oyz) một góc 60{^\circ}. Tính tổng a + b + c? (Làm tròn đến hàng phần trăm)?

    Hướng dẫn:

    Mặt phẳng (P) đi qua 2 điểm A, B nên ta có: \left\{ \begin{matrix} b - 1 = 0 \\ a - 1 = 0 \end{matrix} \right.\ \Rightarrow a = b = 1

    Và (P)tạo với (Oyz) một góc 60{^\circ} nên \cos\left( (P);(Oyz) \right) = \frac{|a|}{\sqrt{a^{2} + b^{2} + c^{2}}.\sqrt{1}} = \frac{1}{2}\ \ \ \ (*)

    Thay a = b = 1 vào phương trình (*) được: \sqrt{2 + c^{2}} = 2 \Rightarrow c = - \sqrt{2}

    Khi đó: a + b + c = 2 - \sqrt{2} \approx 0,59

  • Câu 14: Nhận biết
    Tính cosin góc giữa hai đường thẳng

    Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng

    d_{1}:\frac{x - 2}{2} = \frac{y}{2} = \frac{z + 1}{- 1} và d_{2}:\frac{x + 1}{1} = \frac{y - 2}{- 2} = \frac{z + 3}{1}. Tính cosin của góc giữa hai đường thẳng d_{1} và d_{2}.

    Hướng dẫn:

    Đường thẳng d_{1} có VTCP \overrightarrow{u_{1}} = (2;2; - 1).

    Đường thẳng d_{2} có VTCP \overrightarrow{u_{2}} = (1; - 2;1).

    Ta có

    \cos\left( d_{1};d_{2} \right) = \left| \cos\left( \overrightarrow{u_{1}};\overrightarrow{u_{2}} \right) \right| = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right|}{\left| \overrightarrow{u_{1}} \right|\left| \overrightarrow{u_{2}} \right|}

    = \frac{|2 - 4 - 1|}{\sqrt{4 + 4 + 1}.\sqrt{1 + 4 + 1}} = \frac{\sqrt{6}}{6}

  • Câu 15: Thông hiểu
    Chọn đáp án đúng

    Trong không gian với hệ tọa độ Oxyz cho A(3;0;1),B(6; - 2;1). Viết phương trình mặt phẳng (P) đi qua A, B và (P) tạo với mặt phẳng (Oyz) góc \alpha thỏa mãn \cos\alpha = \frac{2}{7}?

    Hướng dẫn:

    Gọi \overrightarrow{n_{P}} = (a;b;c);\left( a^{2} + b^{2} + c^{2} \neq 0 \right)

    Ta có:

    A,B \in (P) \Rightarrow \overrightarrow{AB}\bot\overrightarrow{n_{P}} \Rightarrow 3a - 2b = 0

    \Leftrightarrow 3a = 2b \Leftrightarrow 9a^{2} = 4b^{2}(1)

    \cos\left( \widehat{(P),(Oyz)} \right) = \frac{2}{7}

    \Rightarrow \frac{\left| \overrightarrow{n_{P}}.\overrightarrow{n_{Oyz}} \right|}{\left| \overrightarrow{n_{P}} \right|.\left| \overrightarrow{n_{Oyz}} \right|} = \frac{|a|}{\sqrt{a^{2} + b^{2} + c^{2}}.\sqrt{1}} = \frac{2}{7}

    \Leftrightarrow \frac{|a|}{\sqrt{a^{2} + \left( \frac{3a}{2} \right)^{2} + c^{2}}} = \frac{2}{7} \Leftrightarrow \frac{|a|}{\sqrt{\frac{13}{4}a^{2} + c^{2}}} = \frac{2}{7}

    \Leftrightarrow a^{2} = \frac{4}{49}\left( \frac{13}{4}a^{2} + c^{2} \right)

    \Leftrightarrow 9a^{2} = c^{2}(2)(1),(2)

    \Rightarrow c^{2} = 4b^{2} \Leftrightarrow \left\lbrack \begin{matrix} c = 2b \\ c = - 2b \end{matrix} \right.

    Chọn: a = 2 \Rightarrow b = 3 \Rightarrow c = 6 \Rightarrow (P):2x + 3y + 6z - 12 = 0

    a = - 2 \Rightarrow b = - 3 \Rightarrow c = 6 \Rightarrow (P):2x + 3y - 6z = 0

  • Câu 16: Vận dụng
    Tính cosin góc giữa hai mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2; - 1),B(0;4;0) và mặt phẳng (P) có phương trình 2x - y - 2z + 2015 = 0. Gọi \alpha là góc nhỏ nhất mà mặt phẳng (Q) đi qua hai điểm A, B tạo với mặt phẳng (P). Giá trị của \cos\alpha là

    Hướng dẫn:

    Ta có:

    (Q) đi qua A nên:

    (Q):a(x - 1) + b(y - 2) + c(z + 1) = 0

    (Q) đi qua B nên:

    a.(0 - 1) + b.(4 - 2) + c.(0 + 1) = 0

    \Rightarrow - a + 2b + c = 0 \Rightarrow a = 2b + c

    \Rightarrow (Q):(2b + c)(x - 1) + b(y - 2) + c(z + 1) = 0

    \Rightarrow \overrightarrow{n_{(Q)}} = (2b + c;b;c)

    (P):2x - y - 2z + 2015 = 0 \Rightarrow \overrightarrow{n_{(P)}} = (2; - 1; - 2)

    \Rightarrow cos\left( \widehat{(P);(Q)} \right) = \left| \cos\left( \overrightarrow{n_{(P)}};\overrightarrow{n_{(Q)}} \right) \right|

    \Rightarrow cos\left( \widehat{(P);(Q)} \right) = \frac{\left| 2(2b + c) - b - 2c \right|}{\sqrt{(2b + c)^{2} + b^{2} + c^{2}}.\sqrt{2^{2} + ( - 1)^{2} + 2^{2}}}

    \Rightarrow cos(\alpha) = \frac{|3b|}{3.\sqrt{5b^{2} + 4bc + 2c^{2}}}

    Ta cần tìm \alpha_{\min} \Leftrightarrow (cos\alpha)_{\max}

    cos\alpha = \frac{|3b|}{3.\sqrt{5b^{2} + 4bc + 2c^{2}}} = \frac{|b|}{\sqrt{3b^{2} + 2(b + c)^{2}}} \leq \frac{1}{\sqrt{3}}

    Dấu " = " xảy ra khi: b = - c .

  • Câu 17: Thông hiểu
    Tìm tham số m thỏa mãn yêu cầu bài toán

    Trong không gian Oxyz, hai đường thẳng d_{1}:\frac{x - 2}{1} = \frac{y + 1}{\sqrt{2}} = \frac{z - 3}{1} và d_{2}:\frac{x + 5}{1} = \frac{y + 3}{\sqrt{2}} = \frac{z - 5}{m} tạo với nhau góc 60^{0}, giá trị của tham số m bằng

    Hướng dẫn:

    Ta có vectơ chỉ phương của hai đường thẳng d_{1};d_{2} lần lượt là \overrightarrow{u_{1}} = \left( 1;\sqrt{2};1 \right) và \overrightarrow{u_{2}} = \left( 1;\sqrt{2};m \right).

    Theo công thức tính góc tạo bởi hai đường thẳng thì \cos\varphi = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right|}{\left| \overrightarrow{u_{1}} \right|.\left| \overrightarrow{u_{2}} \right|} với \varphi = \widehat{\left( d_{1};d_{2} \right)}.

    Từ giả thiết suy ra

    \frac{1}{2} = \frac{|3 + m|}{2\sqrt{m^{2} + 3}} \Leftrightarrow \sqrt{m^{2} + 3} = |3 + m|

    \Leftrightarrow m^{2} + 3 = (3 + m)^{2}

    \Leftrightarrow m^{2} + 3 = m^{2} + 6m + 9 \Leftrightarrow m = - 1

  • Câu 18: Thông hiểu
    Tính sin góc giữa hai đối tượng

    Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x - 2y + 2z - 3 = 0 và đường thẳng d:\frac{x}{2} = \frac{y}{- 1} = \frac{z}{1}. Tính số đo của góc giữa đường thẳng d và mặt phẳng (P).

    Hướng dẫn:

    Mặt phẳng (P) có VTPT \overrightarrow{n_{(P)}} = (1; - 2;2).

    Đường thẳng d có VTCP \overrightarrow{u_{d}} = (2; - 1;1).

    Gọi \varphi là góc giữa đường thẳng d và mặt phẳng (P).

    Ta có \sin\varphi = \left| \cos\left( \overrightarrow{n_{\alpha}};\overrightarrow{u_{d}} \right) \right| = \frac{\sqrt{6}}{3}

  • Câu 19: Thông hiểu
    Tìm tham số m thỏa mãn yêu cầu

    Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d_{1}:\left\{ \begin{matrix} x = - 1 + t \\ y = - \sqrt{2}t \\ z = 2 + t \\ \end{matrix} \right. và d_{2}:\left\{ \begin{matrix} x = 2 + t \\ y = 1 + \sqrt{2}t \\ z = 2 + mt \\ \end{matrix} \right..Tìm giá trị của tham số m để hai đường thẳng hợp với nhau một góc bằng 60^{0}?

    Hướng dẫn:

    Đường thẳng d_{1} có VTCP \overrightarrow{u_{1}} = \left( 1; - \sqrt{2};1 \right), d_{2} có VTCP \overrightarrow{u_{2}} = \left( 1;\sqrt{2};m \right).

    Do đó

    \cos60^{0} = \cos\left( d_{1};d_{2} \right) \Leftrightarrow \frac{1}{2} = \left| \cos\left( \overrightarrow{u_{1}};\overrightarrow{u_{2}} \right) \right|

    \Leftrightarrow \frac{1}{2} = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right|}{\left| \overrightarrow{u_{1}} \right|\left| \overrightarrow{u_{2}} \right|} \Leftrightarrow \frac{1}{2} = \frac{|m - 1|}{2\sqrt{m^{2} + 3}} \Leftrightarrow m = - 1.

  • Câu 20: Thông hiểu
    Chọn đáp án đúng

    Trong không gian Oxyz cho đường thẳng \Delta:\frac{x}{1} = \frac{y}{2} = \frac{z}{- 1} và mặt phẳng (\alpha):x - y + 2z = 0. Tính góc giữa đường thẳng \Delta và mặt phẳng (\alpha)?

    Hướng dẫn:

    Đường thẳng  \Delta  có vectơ chỉ phương \overrightarrow{u} = (1;2; - 1), mặt phẳng (\alpha) có vectơ pháp tuyến \overrightarrow{n} = (1; - 1;2).

    Gọi \varphi là góc giữa đường thẳng \Delta và mặt phẳng(\alpha), khi đó

    \sin(\varphi) = \left| \cos\left( \overrightarrow{n};\overrightarrow{u} \right) \right| = \frac{\left| \overrightarrow{u}.\overrightarrow{n} \right|}{\left| \overrightarrow{u} \right|\left| \overrightarrow{n} \right|}

    = \frac{|1 - 2 - 2|}{\sqrt{6}.\sqrt{6}} = \frac{1}{2} \Rightarrow \varphi = 30^{0}

  • Câu 21: Thông hiểu
    Tính số đo góc giữa đường thẳng và mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:\left\{ \begin{matrix} x = 1 - t \\ y = 2 + 2t \\ z = 3 + t \\ \end{matrix} \right.\ ;\left( t\mathbb{\in R} \right) và mặt phẳng (P):x - y + 3 = 0. Tính số đo góc giữa đường thẳng d và mặt phẳng (P).

    Hướng dẫn:

    Đường thẳng d có véc tơ chỉ phương là \overrightarrow{u} = ( - 1;2;1)

    Mặt phẳng (P) có véc tơ pháp tuyến là \overrightarrow{n} = (1; - 1;0)

    Gọi \alpha là góc giữa đường thẳng d và mặt phẳng (P).

    Khi đó ta có

    \sin\alpha = \frac{\left| \overrightarrow{u}.\overrightarrow{n} \right|}{\left| \overrightarrow{u} \right|\left| \overrightarrow{n} \right|} = \frac{3}{2\sqrt{3}} = \frac{\sqrt{3}}{2}

    Do đó \alpha = 60^{0}

  • Câu 22: Thông hiểu
    Tính góc tạo bởi mặt phẳng và trục Ox

    Trong không gian Oxyz, cho mặt phẳng (P): - \sqrt{3}x + y + 1 = 0. Tính góc tạo bởi (P) với trục Ox?

    Hướng dẫn:

    Mặt phẳng (P) có VTPT \overrightarrow{n} = \left( - \sqrt{3};1;0 \right)

    Trục Ox có VTCP \overrightarrow{i} = (1;0;0)

    Góc tạo bởi (P) với trục Ox

    \sin\left( (P);Ox \right) = \left| \cos\left( (P);Ox \right) \right| = \frac{\left| \overrightarrow{n}.\overrightarrow{i} \right|}{\left| \overrightarrow{i} \right|\left| \overrightarrow{n} \right|} = \frac{\sqrt{3}}{2}

    Vậy góc tạo bởi (P) với trục Ox bằng 60^{()}.

  • Câu 23: Vận dụng
    Tính góc giữa đường thẳng và mặt phẳng

    Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, thỏa mãn điều kiện, AB = BC = a,AD = 2a, SA vuông góc với mặt đáy (ABCD), SA = a. Gọi M,N lần lượt là trung điểm của SB,CD. Tính cosin của góc giữa MN và (SAC). (Làm tròn kết quả đến hàng phần trăm)

    Hướng dẫn:

    Chọn hệ trục tọa độ như hình vẽ

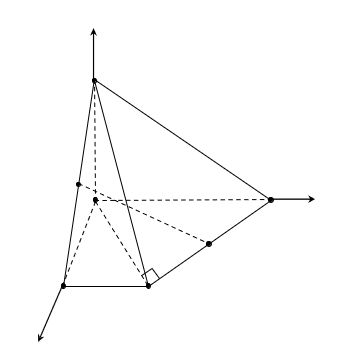
    Chọn đơn vị là a

    Có A(0;0;0),B(1;0;0),C(1;1;0),D(0;2;0),S(0;0;1),M\left( \frac{1}{2};0;\frac{1}{2} \right),N\left( \frac{1}{2};\frac{3}{2};0 \right).

    Vecto chỉ phương của \overrightarrow{MN}là \overrightarrow{MN} = \left( 0;\frac{3}{2};\frac{- 1}{2} \right) \Rightarrow 2\overrightarrow{MN} = (0;3; - 1)

    Vecto pháp tuyến của (SAC)là \overrightarrow{n} = \left\lbrack \overrightarrow{AC},\overrightarrow{AS} \right\rbrack = (1; - 1;0)

    Vậy \sin\left( MN,(SAC) \right) = \frac{|3|}{\sqrt{9 + 1}.\sqrt{2}} = \frac{3\sqrt{5}}{10}

    Suy ra: \cos\left( MN,(SAC) \right) = \sqrt{1 - \left( \frac{3\sqrt{5}}{10} \right)^{2}} = \frac{\sqrt{55}}{10} \approx 0,74

  • Câu 24: Thông hiểu
    Tính góc giữa đường thẳng và mặt phẳng

    Trong không gian với hệ tọa độ Oxyz cho đường thẳng d:\left\{ \begin{matrix} x = 1 - t \\ y = 2 + 2t \\ z = 3 + t \\ \end{matrix} \right. và mặt phẳng (P):x - y + 3 = 0. Tính số đo góc giữa đường thẳng d và mặt phẳng (P).

    Hướng dẫn:

    Đường thẳng (d) có vectơ chỉ phương là: \overrightarrow{u} = ( - 1;2;1).

    Mặt phẳng (P) có vectơ pháp tuyến là: \overrightarrow{n} = (1; - 1;0).

    Khi đó: \sin\alpha = \frac{\left| \overrightarrow{u};\overrightarrow{n} \right|}{\left| \overrightarrow{u} \right|.\left| \overrightarrow{n} \right|} = \frac{\sqrt{3}}{2}

    Vậy \alpha = 60^{0}.

  • Câu 25: Thông hiểu
    Chọn phương án đúng

    Cho mặt phẳng (P):3x + 4y + 5z + 8 = 0 và đường thẳng d là giao tuyến của hai mặt phẳng: (\alpha):x - 2y + 1 = 0 và (\beta):x - 2z - 3 = 0. Gọi \varphi là góc giữa đường thẳng d và mặt phẳng (P). Khi đó:

    Hướng dẫn:

    Ta có: \overrightarrow{u_{d}} = \left\lbrack \overrightarrow{n_{\alpha}};\overrightarrow{n_{\beta}} \right\rbrack = (4;2;2)

    \sin\left( d;(P) \right) = \left| \cos\left( \overrightarrow{u_{d}};\overrightarrow{n_{(P)}} \right) \right| = \frac{\sqrt{3}}{2} \Rightarrow \varphi = 60^{0}.

  • Câu 26: Nhận biết
    Tính góc giữa hai đường thẳng

    Trong không gian Oxyz, cho hai đường thẳng \Delta_{1}:\frac{x - 1}{- 2} = \frac{y + 2}{1} = \frac{z - 3}{2} và \Delta_{2}:\frac{x + 3}{1} = \frac{y - 1}{1} = \frac{z + 2}{- 4}. Góc giữa hai đường thẳng \Delta_{1};\Delta_{2} bằng?

    Hướng dẫn:

    Véc tơ chỉ phương của \Delta_{1} là \overrightarrow{u_{1}} = ( - 2;1;2)

    Véc tơ chỉ phương của \Delta_{2} là \overrightarrow{u_{2}} = (1;1; - 4)

    \cos\left( \Delta_{1};\Delta_{2} \right) = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right|}{\left| \overrightarrow{u_{1}} \right|.\left| \overrightarrow{u_{2}} \right|} = \frac{\sqrt{2}}{2}.

    Do đó góc giữa hai đường thẳng \Delta_{1} và \Delta_{2} là 45^{0}

  • Câu 27: Thông hiểu
    Tìm số đo góc ABC

    Trong không gian hệ tọa độ Oxyz, cho các điểm A( - 1;2;4),B( - 1;1;4),C(0;0;4). Tìm số đo của \widehat{ABC}.

    Hướng dẫn:

    Ta có:

    A( - 1;2;4),B( - 1;1;4),C(0;0;4)

    \Rightarrow \overrightarrow{AB} = (0; - 1;0);\overrightarrow{BC} = (1; - 1;0)

    \cos\left( \overrightarrow{AB},\overrightarrow{BC} \right) = \frac{\overrightarrow{AB}.\overrightarrow{BC}}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{BC} \right|} = \frac{1}{\sqrt{2}}

    \Rightarrow 180{^\circ} - ABC = 45{^\circ} \Rightarrow ABC = 135{^\circ}

  • Câu 28: Thông hiểu
    Chọn phương án thích hợp

    Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d_{1}:\left\{ \begin{matrix} x = - t \\ y = - 1 + 4t \\ z = 3t \\ \end{matrix} \right. và d_{2}:\frac{x}{1} = \frac{y + 8}{- 4} = \frac{z + 3}{- 3}. Xác định góc giữa hai đường thẳng d_{1} và d_{2}.

    Hướng dẫn:

    Đường thẳng d_{1} có VTCP \overrightarrow{u_{1}} = ( - 1;4;3), d_{2} có VTCP \overrightarrow{u_{2}} = (1; - 4; - 3) = - \overrightarrow{u_{1}}.

    Vậy đáp án cần tìm là: 0^{0}

  • Câu 29: Nhận biết
    Tính góc giữa hai mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - y + z + 2 = 0 và (Q):x + y + 2z - 1 = 0. Góc giữa (P) và (Q) là

    Hướng dẫn:

    Góc giữa (P) và (Q) là: \overrightarrow{n_{P}} = (2; - 1;1);\overrightarrow{n_{Q}} = (1;1;2)

    \cos(\alpha) = \frac{\left| \overrightarrow{n_{P}}.\overrightarrow{n_{Q}} \right|}{\left| \overrightarrow{n_{P}} \right|\left| \overrightarrow{n_{Q}} \right|}

    = \frac{\left| 2.1 + ( - 1).1 + 1.2 \right|}{\sqrt{2^{2} + ( - 1)^{2} + 1^{2}.\sqrt{1^{2} + 1^{2} + 2^{2}}}} = \frac{1}{2}

    \Rightarrow \alpha = 60{^\circ}

  • Câu 30: Thông hiểu
    Chọn công thức đúng

    Góc của đường thẳng (D):\frac{x - x_{0}}{a_{1}} = \frac{y - y_{0}}{a_{2}} = \frac{z - z_{0}}{a_{3}}; \left( a_{1}, a_{2}, a_{3} \neq \ 0 \right) và mặt phẳng (P): Ax + By + Cz + D = 0 ;\left( A^{2} + B^{2} + C^{2} > 0 \right) tính bởi công thức nào sau đây?

    Hướng dẫn:

    Công thức đúng là: \sin\alpha = \frac{\left| Aa_{1} + Ba_{2} + Ca_{3} \right|}{\sqrt{A^{2} + B^{2} + C^{2}}.\sqrt{{a_{1}}^{2} + {a_{2}}^{2} + {a_{3}}^{2}}}

  • Câu 31: Vận dụng
    Tính giá trị của biểu thức P

    Trong không gian Oxyz cho hai đường thẳng d_{1}:\ \frac{x}{- 1} = \frac{y + 1}{2} = \frac{z}{2},\ \ d_{2}:\ \left\{ \begin{matrix} x = 2t \\ y = 1 \\ z = 1 - t \end{matrix} \right.. Gọi \varphi là góc giữa hai đường thẳng d_{1},\ d_{2}. Giá trị \cos\varphi có dạng \frac{a\sqrt{c}}{b}. Tính giá trị biểu thức P = b - 3a + c ?

    Hướng dẫn:

    Ta có {\overrightarrow{u}}_{d_{1}} = ( - 1;\ 2;\ 2),\ {\overrightarrow{u}}_{d_{2}} = (2;\ 0;\ - 1)

    Khi đó \cos\varphi = \frac{\left|{\overrightarrow{u}}_{d_{1}}.{\overrightarrow{u}}_{d_{2}}\right|}{\left| {\overrightarrow{u}}_{d_{1}} \right|\left|{\overrightarrow{u}}_{d_{2}} \right|}

    = \frac{\left| - 1.2 + 2.0 + 2.( -1) \right|}{\sqrt{( - 1)^{2} + 2^{2} + 2^{2}}.\sqrt{2^{2} + 0^{2} + ( -1)^{2}}}= \frac{4}{3\sqrt{5}} = \frac{4\sqrt{5}}{15}.

    Vậy a = 4,b = 15,c = 5\Rightarrow b - 3a+ c = 15 - 3.4 + 5 = 8

0/31
31 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (23%):
    2/3
  • Thông hiểu (61%):
    2/3
  • Vận dụng (16%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
26 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Chuyên đề Toán 12
Xem thêm