VnDoc.com

Chuyên đề Toán 12 Ứng dụng hình học tích phân tính diện tích hình phẳng

Ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Giải nhanh bài toán diện tích hình phẳng bằng tích phân

A. Đề bài trắc nghiệm Ứng dụng hình học tích phân tính diện tích hình phẳng
B. Đáp án tổng quan bài tập trắc nghiệm
C. Hướng dẫn giải chi tiết bài tập trắc nghiệm

Trong Toán 12, chuyên đề ứng dụng hình học của tích phân để tính diện tích hình phẳng là một phần kiến thức quan trọng, thường xuyên xuất hiện trong đề thi THPT quốc gia môn Toán. Đây là nội dung giúp học sinh rèn luyện khả năng kết hợp giữa giải tích và hình học, từ đó tìm ra diện tích các miền phẳng giới hạn bởi đồ thị hàm số. Bài viết này sẽ cung cấp cho bạn công thức, phương pháp giải nhanh và các dạng bài tập tiêu biểu, hỗ trợ việc ôn thi hiệu quả và đạt kết quả cao.

A. Đề bài trắc nghiệm Ứng dụng hình học tích phân tính diện tích hình phẳng

Câu 1: Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2}$ , trục hoành , các đường thẳng , .

A. $S = \frac{7}{3}$ B. $S = \frac{5}{3}$ C. $S = \frac{3}{5}$ D. $S = \frac{3}{7}$

Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = (x - 2)^{2} - 1$ , trục hoành và hai đường thẳng $x = 1,\ x = 2$ .

A. $S = \frac{1}{3}$ B. $S = \frac{2}{3}$ C. D. $S = \frac{4}{3}$

Câu 3: Tính diện tích của hình phẳng giới hạn bởi $y = x^{2} - 2x$ , , , .

A. B. C. D.

Câu 4: Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số $y = x^{3} - 1$ , trục hoành, trục tung và đường thẳng .

A. $S = \frac{7}{2}$ B. $S = \frac{5}{2}$ C. $S = \frac{1}{2}$ D. $S = \frac{3}{2}$

Câu 5: Hình phẳng giới hạn bởi các đường cong và $y = x^{3} - x$ có diện tích bằng $\frac{a}{b}$ là phân số tối giản. Kết luận nào sau đây đúng?

A. B.

C. D.

Câu 6: Trường Nguyễn Văn Trỗi muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là mét, chiều rộng tiếp giáp với mặt đất là mét. Giá thuê mỗi mét vuông là đồng. Vậy số tiền nhà trường phải trả là bao nhiêu đồng?

A. đồng B. đồng

C. đồng D. đồng

Câu 7: Một cổng chào có dạng hình Parabol chiều cao $18\ \ m$ , chiều rộng chân đế $12\ \ m$ . Người ta căng hai sợi dây trang trí , nằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số $\frac{AB}{CD}$ bằng:

A. $\frac{AB}{CD} = \frac{1}{2}$ B. $\frac{AB}{CD} = \frac{1}{\sqrt[3]{2}}$

C. $\frac{AB}{CD} = 2$ D. $\frac{AB}{CD} = \sqrt[3]{2}$

Câu 8: Một họa tiết hình cánh bướm như hình vẽ bên.

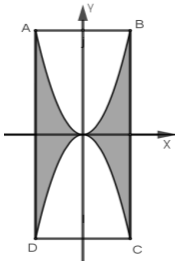
Phần tô đậm được đính đá với giá thành $500.000đ/m^{2}$ . Phần còn lại được tô màu với giá thành $250.000đ/m^{2}$ . Cho Hỏi để trang trí họa tiết như vậy cần số tiền bỏ ra là bao nhiêu?

A. đồng B. đồng

C. đồng D. đồng

Câu 9: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết cm, cm. Biết giá trang trí hoa văn $1cm^{2}$ là 50.000 đồng, tính số tiền cần bỏ ra để trang trí hoa văn đó.

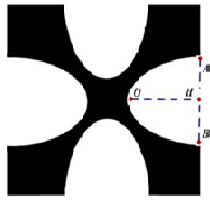
A. đồng B. đồng

C. đồng D. đồng

Câu 10: Một viên gạch hoa hình vuông cạnh . Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ dưới).

Tính diện tích mỗi cánh hoa của viên gạch.

A. $\frac{400}{3}\left( cm^{2} \right)$ B. $\frac{500}{3}\left( cm^{2} \right)$ C. $100\left( cm^{2} \right)$ D. $150\left( cm^{2} \right)$

Câu 11: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2} + 2$ và ?

A. 1 B. $\frac{1}{4}$ C. $\frac{1}{6}$ D. $\frac{1}{2}$

Câu 12: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \frac{x + 1}{x - 2}$ và các trục tọa độ. Chọn kết quả đúng?

A. B. $3ln\frac{3}{2}$ C. $3ln\frac{3}{2} - 2$ D. $3ln\frac{3}{2} - 1$

Câu 13: Cho hàm số $f(x) = x^{3} - 3x^{2} + 2x$ . Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số , trục tung, trục hoành và đường thẳng ?

A. $S = \frac{10}{4}$ B. $S = \frac{12}{4}$ C. $S = \frac{11}{4}$ D. $S = \frac{9}{4}$

Câu 14: Tính diện tích hình phẳng S giới hạn bởi đồ thị các hàm số $y = 2^{x}$ và , trục hoành và trục tung.

A. $S = \frac{5}{2} - \frac{1}{ln2}$ B. C. $S = 2 - \frac{1}{ln2}$ D.

Câu 15: Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị , , , , ?

A. $S = \int_{a}^{b}\left( f(x) - g(x) \right)dx$ B. $S = \int_{a}^{b}{\left| f(x) - g(x) \right|dx}$

C. $S = \int_{a}^{b}{\left( f(x) - g(x) \right)^{2}dx}$ D. $S = \int_{a}^{b}{\left( f^{2}(x) - g^{2}(x) \right)dx}$

B. Đáp án tổng quan bài tập trắc nghiệm

1 - A	2 - B	3 - A	4 - A	5 - C	6 - D	7 – B
8 - A	9 - A	10 - A	11 - C	12 - D	13 - C	14 – A
15 - B	16 - B	17 - A	18 - B	19 - C	20 - B	21 - D

C. Hướng dẫn giải chi tiết bài tập trắc nghiệm

Câu 1:

Diện tích hình phẳng là $S = \int_{1}^{2}{\left| x^{2} \right|dx} = \int_{1}^{2}{x^{2}dx} = \left. \ \frac{x^{3}}{3} \right|_{1}^{2} = \frac{8}{3} - \frac{1}{3} = \frac{7}{3}$ .

Câu 2:

Xét phương trình $(x - 2)^{2} - 1 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 3 \end{matrix} \right.$ .

Ta có:

$S = \int_{1}^{2}{\left| (x - 2)^{2} - 1 \right|dx} = \int_{1}^{2}{\left| x^{2} - 4x + 3 \right|dx}$

$= \left| \int_{1}^{2}{\left( x^{2} - 4x + 3 \right)dx} \right| = \frac{2}{3}.$

Câu 3:

Xét phương trình hoành độ giao điểm: $x^{2} - 2x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \end{matrix} \right.$ .

Diện tích: $S = \int_{- 4}^{1}{\left| x^{2} - 2x \right|dx}$

$= \int_{- 4}^{0}{\left( x^{2} - 2x \right)dx} - \int_{0}^{1}{\left( x^{2} - 2x \right)dx}$

$= \left. \ \left( \frac{x^{3}}{3} - x^{2} \right) \right|_{- 4}^{0} - \left. \ \left( \frac{x^{3}}{3} - x^{2} \right) \right|_{0}^{1} = 38$ .

Câu 4:

Phương trình hoành độ giao điểm $x^{3} - 1 = 0 \Leftrightarrow x = 1$ .

$S = \int_{0}^{2}\left| x^{3} - 1 \right|\ dx = \int_{0}^{1}\left| x^{3} - 1 \right|dx + \int_{1}^{2}\left| x^{3} - 1 \right|dx$

$= \int_{0}^{1}\left( 1 - x^{3} \right)dx + \int_{1}^{2}\left( x^{3} - 1 \right)dx$

$= \left. \ \left( x - \frac{x^{4}}{4} \right) \right|_{0}^{1} + \left. \ \left( \frac{x^{4}}{4} - x \right) \right|_{1}^{2} = \frac{7}{2}$ .

Câu 5:

Ta có: $x(1 - x) = x^{3} - x \Leftrightarrow x^{3} + x^{2} - 2x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = - 2 \\ x = 1 \end{matrix} \right.$

Gọi là diện tích hình phẳng giới hạn bởi các đường cong và $y = x^{3} - x$ .

Khi đó $S = \int_{- 2}^{1}{\left| x^{3} + x^{2} - 2x \right|dx}$

$= \int_{- 2}^{0}{\left| x^{3} + x^{2} - 2x \right|dx} + \int_{0}^{1}{\left| x^{3} + x^{2} - 2x \right|dx}$

$= \left| \int_{- 2}^{0}{\left( x^{3} + x^{2} - 2x \right)dx} \right| + \left| \int_{0}^{1}{\left( x^{3} + x^{2} - 2x \right)dx} \right|$

$= \frac{8}{3} + \frac{5}{12} = \frac{37}{12}$ (đvdt).

Câu 6:

Gọi phương trình parabol $(P):y = ax^{2} + bx + c$ . Do tính đối xứng của parabol nên ta có thể chọn hệ trục tọa độ sao cho có đỉnh $I \in Oy$ (như hình vẽ).

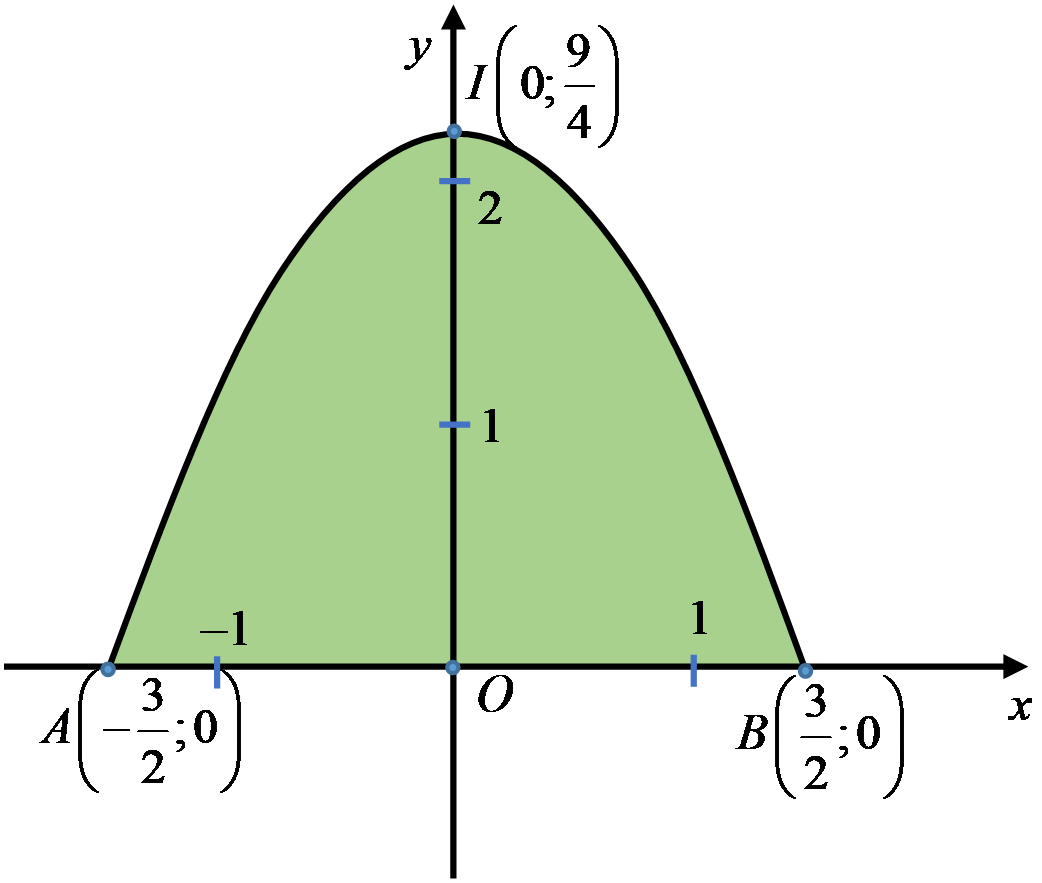
Ta có hệ phương trình:

$\left\{ \begin{matrix} \frac{9}{4} = c,\left( I \in (P) \right) \\ \frac{9}{4}a - \frac{3}{2}b + c = 0\left( A \in (P) \right) \\ \frac{9}{4}a + \frac{3}{2}b + c = 0\left( B \in (P) \right) \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} c = \frac{9}{4} \\ a = - 1 \\ b = 0 \end{matrix} \right.$ .

Vậy $(P):y = - x^{2} + \frac{9}{4}$ .

Dựa vào đồ thị, diện tích cửa parabol là:

$S = \int_{\frac{- 3}{2}}^{\frac{3}{2}}{\left( - x^{2} + \frac{9}{4} \right)dx} = 2\int_{0}^{\frac{3}{2}}{\left( - x^{2} + \frac{9}{4} \right)dx}$

$= \left. \ 2\left( \frac{- x^{3}}{3} + \frac{9}{4}x \right) \right|_{0}^{\frac{9}{4}} = \frac{9}{2}m^{2}$ .

Số tiền phải trả là: $\frac{9}{2}.1500000 = 6750000$ đồng.

Câu 7:

Chọn hệ trục tọa độ như hình vẽ.

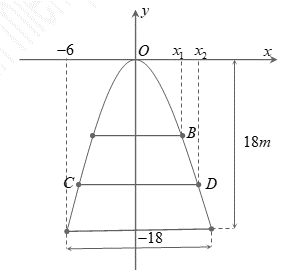
Phương trình Parabol có dạng $y = a.x^{2}$ .

đi qua điểm có tọa độ suy ra: $- 18 = a.( - 6)^{2}$

$\Leftrightarrow a = - \frac{1}{2}$ $\Rightarrow (P):y = - \frac{1}{2}x^{2}$ .

Từ hình vẽ ta có: $\frac{AB}{CD} = \frac{x_{1}}{x_{2}}$ .

Diện tích hình phẳng giới bạn bởi Parabol và đường thẳng $AB:y = - \frac{1}{2}x_{1}^{2}$ là

$S_{1} = 2\int_{0}^{x_{1}}{\left\lbrack - \frac{1}{2}x^{2} - \left( - \frac{1}{2}x_{1}^{2} \right) \right\rbrack dx}\left. \ = 2\left( - \frac{1}{2}.\frac{x^{3}}{3} + \frac{1}{2}x_{1}^{2}x \right) \right|_{0}^{x_{1}} = \frac{2}{3}x_{1}^{3}$ .

Diện tích hình phẳng giới hạn bởi Parabol và đường thẳng $y = - \frac{1}{2}x_{2}^{2}$ là

$S_{2} = 2\int_{0}^{x_{2}}{\left\lbrack - \frac{1}{2}x^{2} - \left( - \frac{1}{2}x_{2}^{2} \right) \right\rbrack dx}\left. \ = 2\left( - \frac{1}{2}.\frac{x^{3}}{3} + \frac{1}{2}x_{2}^{2}x \right) \right|_{0}^{x_{2}} = \frac{2}{3}x_{2}^{3}$

Từ giả thiết suy ra $S_{2} = 2S_{1} \Leftrightarrow x_{2}^{3} = 2x_{1}^{3} \Leftrightarrow \frac{x_{1}}{x_{2}} = \frac{1}{\sqrt[3]{2}}$ . Vậy $\frac{AB}{CD} = \frac{x_{1}}{x_{2}} = \frac{1}{\sqrt[3]{2}}$ .

Câu 8:

Vì $AB = 4dm;BC = 8dm. \Rightarrow A( - 2;4),B(2;4),C(2; - 4),D( - 2; - 4)$ .

Parabol là: $y = x^{2}$ hoặc $y = - x^{2}$

Diện tích phần tô đậm là $S_{1} = 4\int_{0}^{2}{x^{2}dx = \frac{32}{3}\begin{matrix} \end{matrix}(dm^{2})}$

Diện tích hình chữ nhật là $S = 4.8 = 32\begin{matrix} \end{matrix}(m^{2})$

Diện tích phần trắng là $S_{2} = S - S_{1} = 32 - \frac{32}{3} = \frac{64}{3}\begin{matrix} \end{matrix}(dm^{2})$

Tổng chi phí trang chí là: $T = \left( \frac{32}{3}.5000 + \frac{64}{3}.2500 \right).1000 \approx 106666667đ$

Câu 9:

Hình vẽ minh họa:

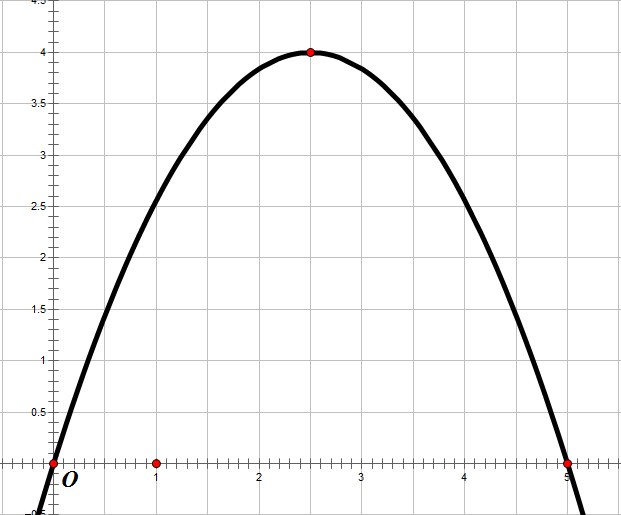
Đưa parabol vào hệ trục ta tìm được phương trình là: $(P):y = - \frac{16}{25}x^{2} + \frac{16}{5}x$ .

Diện tích hình phẳng giới hạn bởi $(P):y = - \frac{16}{25}x^{2} + \frac{16}{5}x$ , trục hoành và các đường thẳng , là:

$S = \int_{0}^{5}\left( - \frac{16}{25}x^{2} + \frac{16}{5}x \right)dx = \frac{40}{3}$ .

Tổng diện tích phần bị khoét đi: $S_{1} = 4S = \frac{160}{3}$ $cm^{2}$ .

Diện tích của hình vuông là: $S_{hv} = 100\ cm^{2}$ .

diện tích bề mặt hoa văn là: $S_{2} = S_{hv} - S_{1} = 100 - \frac{160}{3} = \frac{140}{3}\ cm^{2}$ .

Vậy số tiền cần bỏ ra để trang trí hoa văn đó là: $\frac{140}{3}.50000 \approx 2333333$ đồng

Câu 10:

Hình vẽ minh họa:

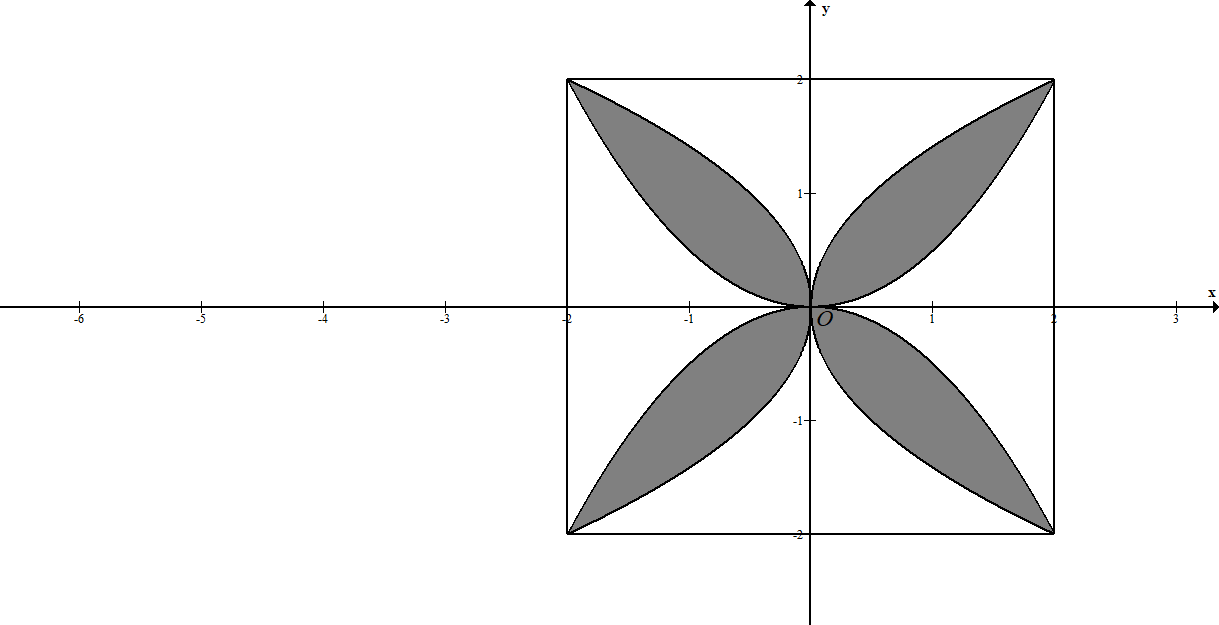
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng ), các cánh hoa tạo bởi các đường parabol có phương trình $y = \frac{x^{2}}{2}$ , $y = - \frac{x^{2}}{2}$ , $x = - \frac{y^{2}}{2}$ , $x = \frac{y^{2}}{2}$ .

Diện tích một cánh hoa (nằm trong góc phàn tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y = \frac{x^{2}}{2}$ , $y = \sqrt{2x}$ và hai đường thẳng .

Do đó diện tích một cánh hoa bằng

$\int_{0}^{2}{\left( \sqrt{2x} - \frac{x^{2}}{2} \right)dx}$ $= \left. \ \left. \ \left( \frac{2\sqrt{2}}{3}\sqrt{(2x)^{3}} - \frac{x^{3}}{6} \right) \right| \right|_{0}^{2}$

$= \frac{4}{3}\left( dm^{2} \right) = \frac{400}{3}\left( cm^{2} \right) = \frac{4}{3}\left( dm^{2} \right) = \frac{400}{3}\left( cm^{2} \right)$ .

-----------------------------------------------------------------------

Có thể khẳng định rằng, chuyên đề Toán 12 ứng dụng hình học tích phân tính diện tích hình phẳng không chỉ giúp học sinh hiểu rõ mối liên hệ giữa giải tích và hình học mà còn nâng cao kỹ năng tư duy tổng hợp, phân tích và trình bày lời giải logic. Đây là dạng toán quen thuộc, thường xuất hiện trong các đề thi từ cơ bản đến nâng cao, đòi hỏi sự thành thạo trong thiết lập công thức tích phân, xử lý miền giới hạn và tính toán chính xác.

Hy vọng bài viết đã cung cấp cho bạn tài liệu ôn luyện hữu ích, giúp hệ thống hóa công thức, phương pháp và dạng bài tập thường gặp. Để đạt hiệu quả cao nhất trong kỳ thi THPT quốc gia môn Toán, hãy kết hợp học lý thuyết với luyện tập qua đề minh họa và đề thi chính thức, từ đó cải thiện tốc độ, nâng cao độ chính xác và tự tin giành điểm số tối ưu.

Tải về

Chọn file muốn tải về: