Trong không gian , cho
. Gọi
là hình chiếu của
trên mặt phẳng
. Khi tứ giác
là hình bình hành thì giá trị
bằng?
là hình chiếu của
trên mặt phẳng
.
là hình bình hành
.
Vậy .
Chinh phục chuyên đề Tọa độ của Vectơ trong không gian lớp 12 với bộ bài tập mức độ vận dụng và vận dụng cao (VD, VDC) được chọn lọc sát với cấu trúc đề thi THPT Quốc gia. Tài liệu được biên soạn kỹ lưỡng, giúp học sinh luyện tập từng bước từ cơ bản đến nâng cao, làm chủ kiến thức về tọa độ, vectơ, hình học không gian và kỹ năng giải nhanh các bài toán trắc nghiệm.
Mỗi bài tập đều kèm theo đáp án và hướng dẫn chi tiết, giúp học sinh dễ dàng tự học, tự kiểm tra và đánh giá năng lực bản thân. Đây là tài liệu không thể thiếu cho học sinh lớp 12 đang trong quá trình ôn thi THPT Quốc gia môn Toán, cũng như các giáo viên cần nguồn tài liệu chất lượng để giảng dạy. Hãy luyện tập thường xuyên để đạt điểm cao trong kỳ thi!
Trong không gian , cho
. Gọi
là hình chiếu của
trên mặt phẳng
. Khi tứ giác
là hình bình hành thì giá trị
bằng?
là hình chiếu của
trên mặt phẳng
.
là hình bình hành
.
Vậy .
Trong không gian điểm
thuộc trục
và cách đều hai điểm
và
là
Ta có:
cách đều hai điểm
khi
Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm đến điểm
trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là gì?
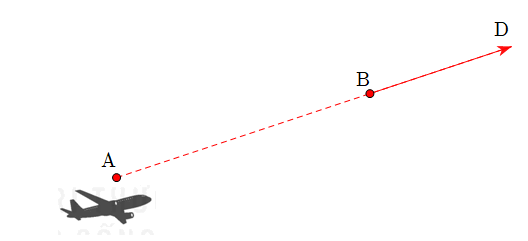
Gọi là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên
và
cùng hướng. Do vận tốc của máy bay không đổi và thời gian bay từ
đến
gấp đôi thời gian bay từ
đến
nên
.
Do đó .
Mặt khác, nên
.
Vậy tọa độ của máy bay sau 5 phút tiếp theo là .
Trong không gian cho ba điểm
và
Để
thẳng hàng thì giá trị
bằng
Ta có
thẳng hàng khi
cùng phương
Vậy
Trong không gian , cho
,
. Điểm
thay đổi thuộc mặt phẳng
. Tính giá trị của biểu thức
khi
nhỏ nhất.
Gọi là điểm thỏa:
.
Ta có:
.
Do đó nhỏ nhất khi và chỉ khi
nhỏ nhất.
Điều này xảy ra khi và chỉ khi là hình chiếu của
lên mặt phẳng
.
Suy ra .
Vậy .
Cho biết máy bay đang bay với vận tốc
(đơn vị:
. Máy bay
ngược hướng và có tốc độ gấp 2 lần tốc độ của máy bay
. Tọa độ vectơ vận tốc
của máy bay
là
Tọa độ vectơ vận tốc của máy bay
là:
Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm đến điểm
trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo
. Khi đó

Gọi là vị trí của máy bay sau 10 phút bay tiếp theo. Vì hướng của máy bay không đổi nên
và
cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ
đến
bằng thời gian bay từ
đến
nên
.
Do đó, .
Mặt khác: nên
Vậy .
Vậy tọa độ của máy bay trong 10 phút tiếp theo là .
Suy ra
Trong không gian , cho hình bình hành
với
,
, và
a. Tọa độ điểm .Sai||Đúng
b. Tọa độ vectơ . Đúng||Sai
c. . Đúng||Sai
d. Nếu hình bình hành, thì
. Đúng||Sai
Trong không gian , cho hình bình hành
với
,
, và
a. Tọa độ điểm .Sai||Đúng
b. Tọa độ vectơ . Đúng||Sai
c. . Đúng||Sai
d. Nếu hình bình hành, thì
. Đúng||Sai
(a) Tọa độ điểm .
Trong không gian , gốc tọa độ
.
» Chọn SAI.
(b) Tọa độ vectơ .
Điểm , suy ra
.
» Chọn ĐÚNG.
(c) .
Ta có . Suy ra vectơ
.
» Chọn ĐÚNG.
(d) Nếu hình bình hành, thì
.
Ta có ,
.
hình bình hành, thì
. Khi đó
.
» Chọn ĐÚNG.
Trong không gian với hệ toạ độ , cho điểm
và vectơ
. Tìm toạ độ điểm
biết rằng
.
Ta có: .
Gọi . Ta có
.
Khi đó .
Vậy .
Trong không gian , cho
và
. Khi
thì giá trị
bằng?
Ta có: .
.
Vậy .
Trong không gian , cho hình lập phương
có cạnh bằng 4, đỉnh
trùng với gốc
, các điểm
lần lượt nằm trên các tia
.
a. Tọa độ của điểm là:
Sai||Đúng
b. Tọa độ của vec tơ là:
Sai||Đúng
c. Tọa độ của vec tơ là:
Đúng||Sai
d. Tọa độ của vec tơ là:
Đúng||Sai
Trong không gian , cho hình lập phương
có cạnh bằng 4, đỉnh
trùng với gốc
, các điểm
lần lượt nằm trên các tia
.
a. Tọa độ của điểm là:
Sai||Đúng
b. Tọa độ của vec tơ là:
Sai||Đúng
c. Tọa độ của vec tơ là:
Đúng||Sai
d. Tọa độ của vec tơ là:
Đúng||Sai
Hình vẽ minh họa
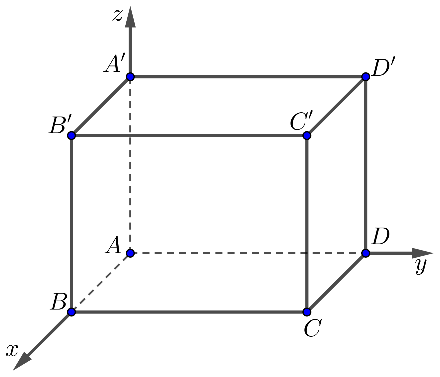
(a) Tọa độ của điểm là:
Do cùng hướng với
và
nên
hay
.
Suy ra: .
» Chọn SAI.
(b) Tọa độ của vec tơ là:
Do cùng hướng với
và
nên
hay
.
Theo quy tắc hình bình hành, ta có: .
Suy ra: .
» Chọn SAI.
(c) Tọa độ của vec tơ là:
Do cùng hướng với
và
nên
hay
.
Suy ra: .
» Chọn ĐÚNG.
(d) Tọa độ của vec tơ là:
.
Theo quy tắc hình hộp, ta có: .
Suy ra:
» Chọn ĐÚNG.
Máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm đến điểm
trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 15 phút tiếp theo bằng bao nhiêu?

Gọi là tọa độ của máy bay sau 15 phút tiếp theo.
Vì máy bay giữ nguyên hướng bay nên và
cùng hướng.
Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ gấp 2 lần thời gian bay từ
nên
Suy ra
Tọa độ của máy bay sau 15 phút tiếp theo là
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là m, chiều rộng là
m và chiều cao là
m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục toạ độ
có gốc
trùng với một góc phòng và mặt phẳng
trùng với mặt sàn, đơn vị đo được lấy theo mét. Hãy tìm toạ độ của điểm treo đèn
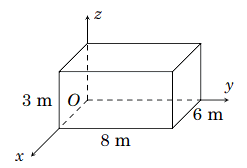
Gọi toạ độ các điểm như hình vẽ dưới đây:
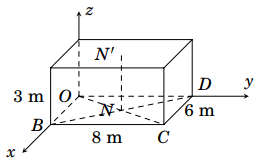
Gọi là trung điểm của
,
là hình chiếu của
lên mặt phẳng trần nhà suy ra
là điểm treo đèn.
Khi đó
Vậy toạ độ của điểm treo đèn là
Trong không gian với hệ tọa độ , cho vectơ
và điểm
. Tọa độ điểm
thỏa mãn
là:
Gọi tọa độ điểm là
, ta có:
.
Ta có:
.
Vậy .
Trong không gian cho hình hộp chữ nhật
có các cạnh
,
,
(xem hình vẽ dưới đây). Tọa độ
. Tính giá trị biểu thức
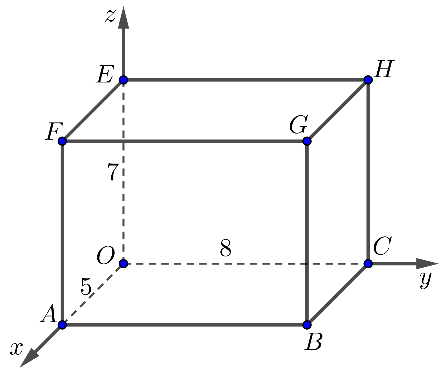
Ta có và hình chiếu của
lên
trùng với
nên
.
.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm và
. Điểm
thỏa mãn
có tọa độ là:
Từ giả thiết nên ba điểm
thẳng hàng và
nằm khác phía so với điểm M do
âm.
Lại có
.
.
Gọi tọa độ , khi đó
Trong không gian với hệ tọa độ , cho hai điểm
và
. Điểm
thỏa mãn
có tọa độ là:
Từ giả thiết nên ba điểm
thẳng hàng và
nằm cùng phía so với điểm
do
dương.
Lại có
.
Vậy B là trung điểm của MA.
Khi đó ta đươc tọa độ điểm .
Cho tứ diện có
là tam giác vuông tại
,
vuông góc với mặt phẳng
và có độ dài bằng 2. Chọn hệ trục tọa độ như hình bên dưới. Điểm
sao cho
là hình bình hành. Khi đó
bằng bao nhiêu?
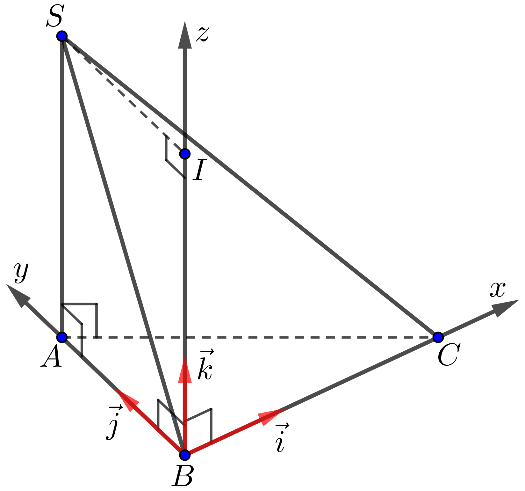
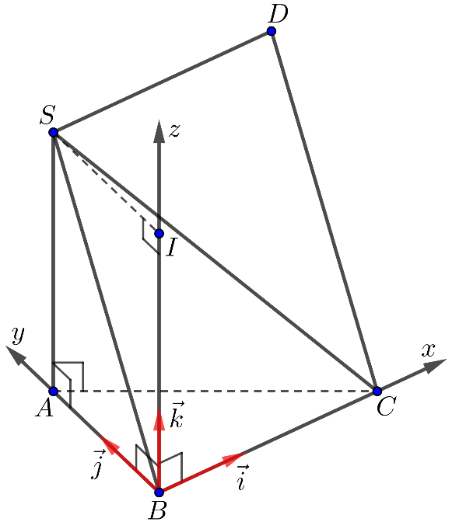
Các vectơ đơn vị trên các trục lần lượt là
có độ dài bằng
.
Vì cùng hướng với
và
nên
Gọi sao cho
là hình bình hành, ta có
cùng hướng với
và
nên
Theo quy tắc hình bình hành, ta có:
Vì cùng hướng với
và
nên
Gọi
Để là hình bình hành thì
Vậy
Trong không gian cho
,
,
. Gọi
là điểm thuộc mặt phẳng
sao cho biểu thức
đạt giá trị nhỏ nhất. Khi đó
có giá trị là
Do thuộc mặt phẳng
nên
.
Ta có ,
,
.
.
Suy ra đạt giá trị nhỏ nhất
khi và chỉ khi
.
Vậy .
Cho hình chóp có đáy
là tam giác đều cạnh bằng
vuông góc với đáy và
bằng 1. Thiết lập hệ tọa độ như hình vẽ bên dưới, tọa độ điểm
. Khi đó
bằng bao nhiêu?
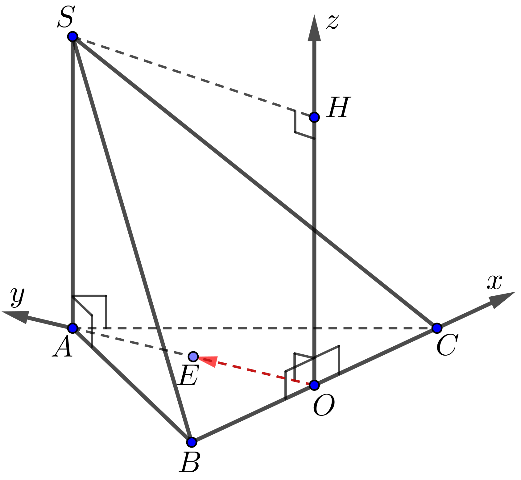
Các vectơ đơn vị trên các trục lần lươt là
với
là điểm thuộc tia
sao cho
và
là điểm thuộc tia
sao cho
.
Vì đều và
nên
là trung điểm cùa
.
Mà nên
và
.
Vì và
cùng hướng và
nên
.
Theo quy tắc hình bình hành, ta có .
Suy ra . Vậy
Trong không gian , cho hình chóp
có đáy
là hình thoi cạnh bằng 5 , giao điểm hai đường chéo
và
trùng với gốc
. Các vectơ
lần lượt cùng hướng với
,
và
như hình bên dưới. Toạ độ vectơ
với
là trung điểm của cạnh
, khi đó
bằng bao nhiêu?
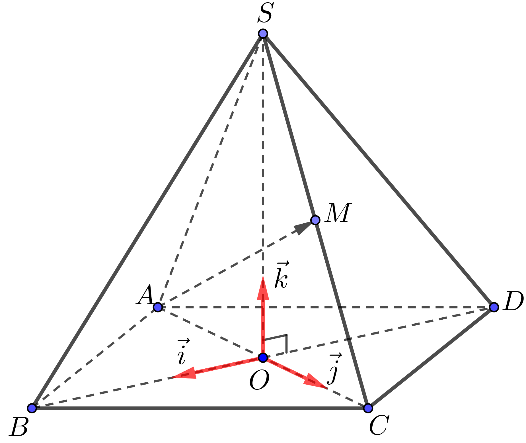
Vì là hình thoi cạnh bằng 5 ,
là giao điểm của
và
nên
là trung điểm của
và
.
Xét vuông tại
, có
.
Vì và
cùng hướng và
nên
.
Vì và
cùng hướng và
nên
.
Ta có
Có mà
và
cùng hướng nên
.
Có và
cùng hướng và
nên
.
Có
Lại có .
Vì là trung điểm của
nên
.
Do đó .
Suy ra
Dưới đây là một giá đỡ chịu hai lực. Biểu diễn từng lực dưới dạng vectơ Descartes

a. Sai||Đúng
b. Đúng||Sai
c. Độ lớn lực tổng hợp lên giá đỡ bằng Đúng||Sai
d. Góc tạo bởi lực tổng hợp lên trục là
Sai||Đúng
Dưới đây là một giá đỡ chịu hai lực. Biểu diễn từng lực dưới dạng vectơ Descartes

a. Sai||Đúng
b. Đúng||Sai
c. Độ lớn lực tổng hợp lên giá đỡ bằng Đúng||Sai
d. Góc tạo bởi lực tổng hợp lên trục là
Sai||Đúng
(a)
Độ lớn lực tác dụng lên từng trục tọa độ Descartes như sau:
» Chọn SAI.
(b)
Cắt mặt phẳng tọa độ lực tác dụng lên trục tọa độ là
là chiều ngang và
là chiều dọc như hình vẽ

Độ lớn lực tác dụng lên trục tọa độ
và
bằng
Cắt mặt phẳng tọa độ lực tác dụng lên trục tọa độ là
là chiều ngang và
là chiều dọc như hình vẽ
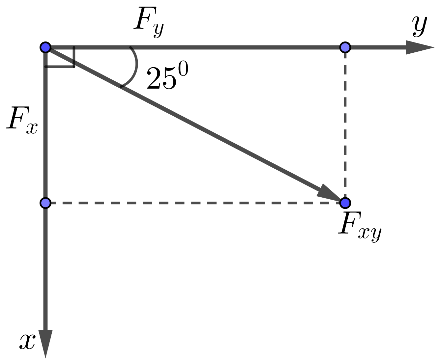
Vậy
» Chọn ĐÚNG.
(c) Độ lớn lực tổng hợp lên giá đỡ bằng
Lực tổng hợp tác dụng lên giá đỡ là :
» Chọn ĐÚNG.
(d) Góc tạo bởi lực tổng hợp lên trục là
Gọi là góc tạo bởi lực tổng hợp lên trục
.
» Chọn SAI.
Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ toạ độ có gốc
trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng
trùng với mặt đất với trục
hướng về phía tây, trục
hướng về phía nam và trục
hướng thẳng đứng lên trời. Sau khi cất cánh và đạt độ cao nhất định, chiếc máy bay duy trì hướng bay về phía nam với tốc độ không đổi là
trong nửa giờ. Xác định toạ độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó đối với hệ toạ độ đã chọn, biết rằng đơn vị đo trong không gian
được lấy theo kilômét.
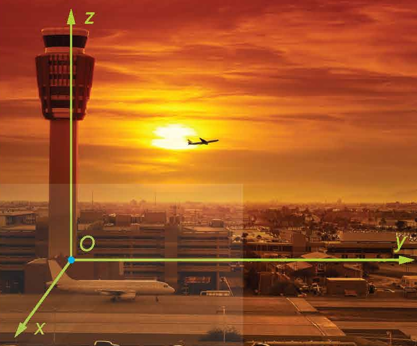
Quãng đường máy bay bay được với vận tốc trong nửa giờ là:
Vì máy bay duy trì hướng bay về phía nam nên tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó với hệ tọa độ đã chọn là
Nếu một vật có khối lượng thì lực hấp dẫn
của trái đất tác dụng lên vật được xác định theo công thức
, trong đó
là gia tốc rơi tự do có độ lớn
. Độ lớn của lực Trái Đất tác dụng lên một quả lê có khối lượng
là
Đổi
Độ lớn của lực hấp dẫn của trái đất tác dụng lên quả lê là:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
