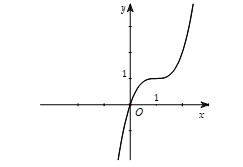Nhận dạng đồ thị hàm số Toán 12
Chuyên đề Toán 12: Khảo sát đồ thị hàm số
Toán 12 Nhận biết dạng đồ thị hàm số vừa được VnDoc.com biên soạn và xin gửi tới bạn đọc để bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.
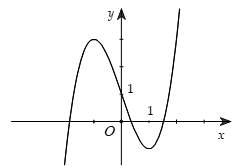
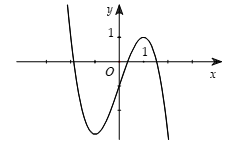
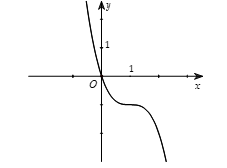
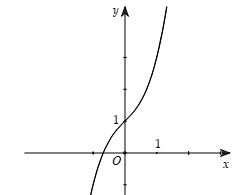
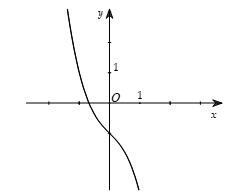
A. Hàm số bậc ba  \(\mathbf{y = a}\mathbf{x}^{\mathbf{3}}\mathbf{+
b}\mathbf{x}^{\mathbf{2}}\mathbf{+ cx + d}\left( \mathbf{a
\neq}\mathbf{0} \right)\)
\(\mathbf{y = a}\mathbf{x}^{\mathbf{3}}\mathbf{+
b}\mathbf{x}^{\mathbf{2}}\mathbf{+ cx + d}\left( \mathbf{a
\neq}\mathbf{0} \right)\)
| TRƯỜNG HỢP |
|
|
Phương trình  \(y' = 0\) có 2 nghiệm phân biệt \(y' = 0\) có 2 nghiệm phân biệt |
|
|
| Phương trình |
|
|
| Phương trình |
|
|
B. Hàm số trùng phương ![]() \(\mathbf{y = a}\mathbf{x}^{\mathbf{4}}\mathbf{+
b}\mathbf{x}^{\mathbf{2}}\mathbf{+ c}\left( \mathbf{a \neq}\mathbf{0}
\right)\)
\(\mathbf{y = a}\mathbf{x}^{\mathbf{4}}\mathbf{+
b}\mathbf{x}^{\mathbf{2}}\mathbf{+ c}\left( \mathbf{a \neq}\mathbf{0}
\right)\)
| TRƯỜNG HỢP | ||
|
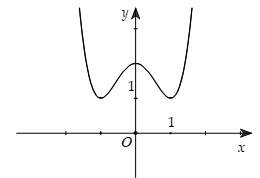
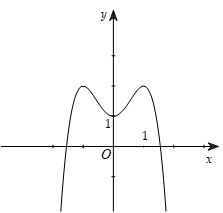
Phương trình (a.b < 0) |
 |
 |
Phương trình  \(y' = 0\) có 1 nghiệm \(y' = 0\) có 1 nghiệm |
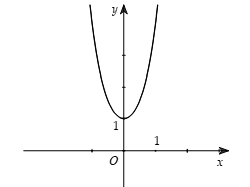 |
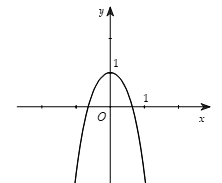 |
C. Hàm số bậc nhất/bậc nhất  \(\mathbf{y =}\frac{\mathbf{ax + b}}{\mathbf{cx +
d}}\mathbf{\ \ \ }\left( \mathbf{c \neq}\mathbf{0,\ }\mathbf{ad - bc
\neq}\mathbf{0} \right)\)
\(\mathbf{y =}\frac{\mathbf{ax + b}}{\mathbf{cx +
d}}\mathbf{\ \ \ }\left( \mathbf{c \neq}\mathbf{0,\ }\mathbf{ad - bc
\neq}\mathbf{0} \right)\)
Tập xác định: ![]() \(D\mathbb{=
R}\backslash\left\{ - \frac{d}{c} \right\}\).
\(D\mathbb{=
R}\backslash\left\{ - \frac{d}{c} \right\}\).
Đạo hàm:  \(y' =
\frac{ad - bc}{(cx + d)^{2}},\forall x \neq - \frac{d}{c}\).
\(y' =
\frac{ad - bc}{(cx + d)^{2}},\forall x \neq - \frac{d}{c}\).
- Nếu
 \(ad - bc > 0\): hàm số đồng biến trên từng khoảng xác định.
\(ad - bc > 0\): hàm số đồng biến trên từng khoảng xác định. - Nếu
 \(ad - bc < 0\): hàm số nghịch biến trên từng khoảng xác định.
\(ad - bc < 0\): hàm số nghịch biến trên từng khoảng xác định.
Giới hạn, tiệm cận
 \(\lim_{x \rightarrow \pm \infty}y =
\lim_{x \rightarrow \pm \infty}\frac{ax + b}{cx + d} =
\frac{a}{c}\) suy ra
\(\lim_{x \rightarrow \pm \infty}y =
\lim_{x \rightarrow \pm \infty}\frac{ax + b}{cx + d} =
\frac{a}{c}\) suy ra  \(y =
\frac{a}{c}\) là tiệm cận ngang của đồ thị hàm số.
\(y =
\frac{a}{c}\) là tiệm cận ngang của đồ thị hàm số. \(\lim_{x \rightarrow - \frac{d}{c}}y =
\lim_{x \rightarrow - \frac{d}{c}}\frac{ax + b}{cx + d} =
\infty\) suy ra
\(\lim_{x \rightarrow - \frac{d}{c}}y =
\lim_{x \rightarrow - \frac{d}{c}}\frac{ax + b}{cx + d} =
\infty\) suy ra  \(x = -
\frac{d}{c}\) là tiệm cận đứng của đồ thị hàm số.
\(x = -
\frac{d}{c}\) là tiệm cận đứng của đồ thị hàm số.
Bảng biến thiên
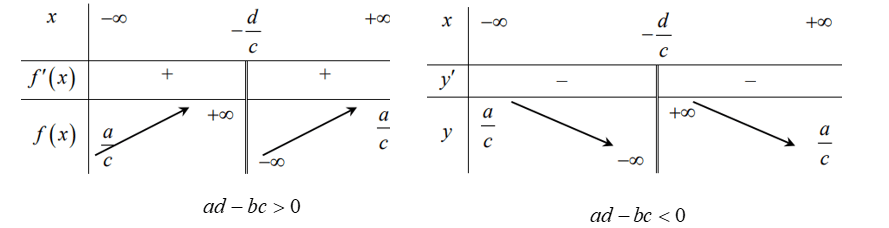
Đồ thị hàm số ![]() \(\mathbf{y =}\frac{\mathbf{ax + b}}{\mathbf{cx +
d}}\mathbf{\ \ \ }\left( \mathbf{c \neq}\mathbf{0,\ }\mathbf{ad - bc
\neq}\mathbf{0} \right)\)
\(\mathbf{y =}\frac{\mathbf{ax + b}}{\mathbf{cx +
d}}\mathbf{\ \ \ }\left( \mathbf{c \neq}\mathbf{0,\ }\mathbf{ad - bc
\neq}\mathbf{0} \right)\)
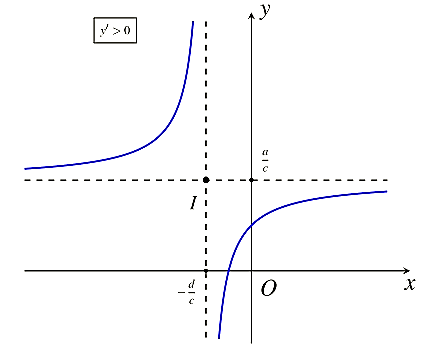 |
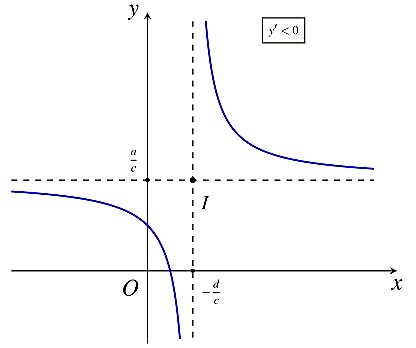 |