Hướng dẫn cách tính Xác suất toàn phần. Công thức Bayes
Cách tính xác suất toàn phần, công thức Bayes - Toán lớp 12
Bạn đang gặp khó khăn khi giải các bài toán xác suất? Đừng lo! Trong thống kê và xác suất, xác suất toàn phần và công thức Bayes là hai công cụ cực kỳ hữu ích để xử lý những tình huống phức tạp, đặc biệt khi cần xác định khả năng xảy ra của một biến cố trong điều kiện có nhiều nguyên nhân. Bài viết này sẽ giúp bạn nắm vững định nghĩa, cách tính xác suất toàn phần, cùng công thức Bayes, qua đó bạn sẽ dễ dàng áp dụng vào bài tập cũng như các tình huống thực tế trong phân tích dữ liệu, trí tuệ nhân tạo hay kiểm định giả thuyết thống kê.
A. Công thức tính xác suất toàn phần. Công thức Bayes
1. Công thức xác suất toàn phần
Cho hai biến cố 
\(A\) và \(B\) với \(\ 0 <
P(B) < 1\), ta có:
\(P(A) = P(AB) + P\left( A\overline{B}
\right) = P(B).P\left( A|B \right) + P\left( \overline{B}
\right).P\left( A|\overline{B} \right)\)
2. Công thức Bayes
Cho hai biến cố \(A\) và \(B\)với \(P(A)
> 0,P(B) > 0\), ta có: \(P\left(
B|A \right) = \frac{P(B).P\left( A|B \right)}{P(A)}\)
Nhận xét:
Cho hai biến cố \(A\) và \(B\)với \(P(A)
> 0,P(B) > 0\), do \(P(A) =
P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left(
A|\overline{B} \right)\)
nên công thức Bayes còn có dạng: \(P\left(
B|A \right) = \frac{P(B).P\left( A|B \right)}{P(B).P\left( A|B \right) +
P\left( \overline{B} \right).P\left( A|\overline{B}
\right)}\)
Chú ý: Khi sử dụng Công thức xác suất toàn phần và Công thức Bayes:
- Công thức xác suất toàn phần và Công thức Bayes được áp dụng trong các trường hợp sự việc bài toán đề cập đến gồm nhiều giai đoạn có sự liên đới nhau trong quá trình xảy ra. Khi áp dụng giải toán, biến cố cần tìm xác suất chi phối bởi hệ đầy đủ biến cố trước đó. Vì vậy, để giải bài toán xác suất này, ta cần:
- Phân tích kỹ đề bài, linh hoạt liên tưởng vào thực tế.
- Xác định được nhóm biến cố đầy đủ ở giai đoạn đầu của sự việc mà bài toán đã đưa ra.
- Gọi tên biến cố xảy ra ở giai đoạn sau liên quan đến nhóm biến cố đầy đủ được xác định trước đó.
- Xác định xác suất của từng biến cố ở hệ đầy đủ, các xác suất có điều kiện của biến cố ở giai đoạn sau với từng biến cố trong hệ đầy đủ.
- Áp dụng công thức xác suất toàn phần nếu biến cố cần tìm xác xuất là biến cố xảy ra ở giai đoạn sau.
- Nếu biết biến cố xảy ra trong giai đoạn sau, để xác định xác suất của một biến cố nào đó ở giai đoạn trước liên quan đến biến cố ở giai đoạn sau như thế nào, ta sử dụng Công thức Bayes.
Yêu cầu cần đạt
- Thông hiểu: Mô tả được công thức xác suất toàn phần, công thức Bayes thông qua bảng dữ liệu thống kê 2x2 và sơ đồ hình cây.
- Vận dụng: Sử dụng được công thức Bayes để tính xác suất có điều kiện.
- Vận dụng cao: Sử dụng được công thức Bayes vận dụng vào một số bài toán thực tiễn.
Sử dụng được sơ đồ hình cây để tính xác suất có điều kiện trong một số bài toán thực tiễn liên quan tới thống kê.
B. Bài tập ví dụ minh họa hướng dẫn tính xác suất
Bài tập 1. Cho sơ đồ hình cây như hình bên dưới:
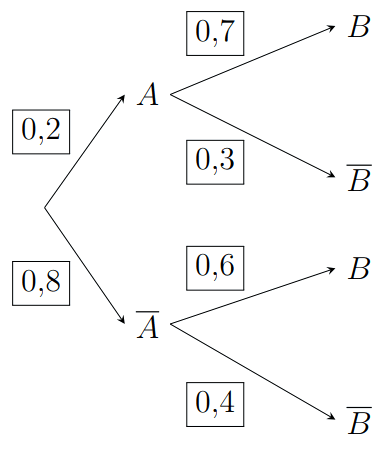
Tính:
a) \(P(B \mid A)\). b) \(P(B)\). c) \(P\left( \overline{B} \right)\).
Hướng dẫn giải
Cách 1.
Dựa vào sơ đồ hình cây, ta có \(P(B \mid A)
= 0,7\).
Xác suất của biến cố \(B\) là \(P(B) = 0,2.0,7 + 0,8.0,6 = 0,62\).
Theo sơ đồ hình hình cây: \(P\left(
\overline{B} \right) = 0,2.0,3 + 0,8.0,4 = 0,38\)
Cách 2: \(P\left( \overline{B} \right) = 1
- P(B) = 0,38\).
Bài tập 2. Một cái hộp có chứa \(40\) quả cầu màu đỏ và \(60\) quả cầu màu vàng; các quả cầu có kích thước và khối lượng như nhau. Sau khi thống kê người ta thấy số lượng các quả cầu được cho trong bảng sau:
|
Màu |
Có đánh số |
Không |
|
Đỏ |
20 |
20 |
|
Vàng |
36 |
24 |
Người ta lấy ngẫu nhiên một quả cầu trong hộp, xét hai biến cố sau:
\(A\): “Quả cầu lấy ra có đánh số”.
\(B\): “Quả cầu lấy ra có màu đỏ”
Sử dụng công thức xác suất toàn phần tính xác suất để quả cầu lấy ra được đánh số.
Hướng dẫn giải
Ta có: \(P(B) = \frac{40}{100} =
\frac{2}{5}\); \(P\left( \overline{B}
\right) = 1 - P(B) = 1 - \frac{2}{5} = \frac{3}{5}\);
\(P\left( A|B \right) = \frac{20}{40} =
\frac{1}{2}\); \(P\left( A|\overline{B}
\right) = \frac{36}{60} = \frac{3}{5}\).
Theo công thức tính xác suất toàn phần ta có xác suất để lấy ra được viên bi được đánh số là
\(P(A) = P(B).P\left( A|B \right) + P\left(\overline{B} \right).P\left( A|\overline{B} \right)\)\(= \frac{2}{5}\ .\frac{1}{2} + \frac{3}{5}\ .\ \frac{3}{5} = \frac{14}{25} =0,56\).
Bài tập 3. Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai. Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.
Hướng dẫn giải
Gọi \(A\) là biến cố “lấy được một viên bi màu xanh ở hộp thứ nhất“ và \(B\) là biến cố “lấy được hai viên bi màu đỏ ở hộp thứ hai”
Khi đó ta có \(P(A) = \frac{1}{3}\), \(P\left( B|A \right) =
\frac{C_{7}^{2}}{C_{11}^{2}} = \frac{21}{55}\).
Suy ra \(P\left( \overline{A} \right) = 1 -
P(A) = \frac{2}{3}\); \(P\left(
B|\overline{A} \right) = \frac{C_{8}^{2}}{C_{11}^{2}} =
\frac{28}{55}\).
Áp dụng công thức xác suất toàn phần ta có
\(P(B) = P(A)P\left( B|A \right) + P\left(
\overline{A} \right)P\left( B|\overline{A} \right) =
\frac{1}{3}.\frac{21}{55} + \frac{2}{3}.\frac{28}{55} =
\frac{7}{15}\).
Bài tập 4. Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất \(0,95\) và một thư đúng (không phải là thư rác) bị chặn với xác suất \(0,01\). Thống kê cho thấy tỉ lệ thư rác là \(3\%\). Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác (kết quả làm tròn đến hàng phần nghìn).
Hướng dẫn giải
Gọi \(A\) là biến cố: “Thư được chọn là thư rác”; \(B\) là biến cố: “Thư được chọn là bị chặn”.
Ta có \(P(A) = 3\% = 0,03\);
\(P\left( \overline{A} \right) = 1 - P(A) =
1 - 0,03 = 0,97\);
\(P\left( B|A \right) = 0,95;\ \ \ P\left(
B|\overline{A} \right) = 0,01\).
Công thức Bayes, ta có:
\(P\left( A|B \right) = \frac{P(A).P\left(B|A \right)}{P(A).P\left( B|A \right) + P\left( \overline{A}\right).P\left( B|\overline{A} \right)}\)\(= \frac{0,03.0,95}{0,03.0,95 +0,97.0,01} \approx 0,746\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1. Trong một trường học, tỉ lệ học sinh nữ là \(52\%\). Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là \(18\%\) và \(15\%\). Chọn ngẫu nhiên một học sinh của trường. Tính xác suất học sinh được chọn có tham gia câu lạc bộ nghệ thuật.
Bài tập 2. Tỉ lệ người dân đã tiêm vắc xin phòng bệnh \(A\) ở một địa phương là \(65\%\). Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh \(A\) là \(5\%\); trong số những người chưa tiêm, tỉ lệ mắc bệnh \(A\) là \(17\%\). Chọn ngẫu nhiên một người ở địa phương đó. Tính xác suất người được chọn mắc bệnh \(A\).
Bài tập 3. Một trạm chỉ phát hai tín hiệu \(A\) và \(B\) với xác suất tương ứng 0,85 và 0,15 do có nhiễu trên đường truyền nên \(\frac{1}{7}\) tín hiệu \(A\) bị méo và thu được như tín hiệu \(B\); còn \(\frac{1}{8}\) tín hiệu \(B\) bị méo thành và thu được như\(A\). Tính xác suất thu được tín hiệu \(A\).
Bài tập 4. Một thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo \(Y\) là \(0,5\%\). Biết rằng, có một loại xét nghiệm mà nếu mắc bệnh hiểm nghèo \(Y\) thì với xác suất \(94\%\) xét nghiệm cho kết quả dương tính; nếu không bị bệnh hiểm nghèo \(Y\) thì với xác suất \(97\%\) xét nghiệm cho kết quả âm tính. Hỏi khi một người xét nghiệm cho kết quả dương tính thì xác suất mắc bệnh hiểm nghèo \(Y\) của người đó là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?
Bài tập 5. Một loại linh kiện do hai nhà máy số I và số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I và II lần lượt là \(4\%\) và \(3\%\). Trong một lô linh kiện để lẫn lộn \(80\) sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó. Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao hơn?
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
-------------------------------------------------
Qua bài viết trên, bạn đã hiểu rõ xác suất toàn phần là gì, biết cách vận dụng công thức Bayes cũng như nắm được phương pháp giải các bài toán xác suất phức tạp một cách logic và hiệu quả. Đây là những kiến thức nền tảng quan trọng không chỉ trong học tập mà còn ứng dụng mạnh mẽ trong khoa học dữ liệu, AI, và phân tích rủi ro. Đừng quên luyện tập thường xuyên qua các ví dụ để hiểu sâu và áp dụng thành thạo hơn!
