Cách tìm điều kiện của m để phương trình có nghiệm Toán 12
Điều kiện của m để phương trình có nghiệm
Trong các dạng toán tham số Toán 12, việc xác định điều kiện của m để phương trình có nghiệm là nội dung trọng tâm, thường được khai thác thông qua ứng dụng tương giao đồ thị hàm số. Dạng toán này không chỉ yêu cầu kỹ năng giải phương trình mà còn đòi hỏi khả năng phân tích hình học của đồ thị. Bài viết sau sẽ giúp bạn nắm rõ cách tiếp cận bản chất, từ đó giải nhanh và chính xác các bài toán điều kiện tham số m.
A. Cách tìm m để phương trình có nghiệm
Phương pháp:
- Bước 1: Cô lập tham số
\(m\) và đưa về dạng \(f(x) = f(m)\). - Bước 2: Khảo sát sự biến thiên của hàm số \(f(x)\) trên \(D\).
- Bước 3: Dựa vào bảng biến thiên để sác định giá trị tham số \(f(m)\) sao cho đường thẳng \(y = f(m)\) nằm ngang vắt đồ thị hàm số \(y = f(x)\).
- Bước 4: Kết luận giá trị của \(f(m)\) để phương trình \(f(x) = f(m)\) có nghiệm trên \(D\).
Chú ý:
⏵Nếu hàm số \(y = f(x)\) có giá trị lớn nhất và giá trị nhỏ nhất trên \(D\) thì phương trình \(f(x) = A(m) \Leftrightarrow
\min_{D}f(x) \leq f(m) \leq \max_{D}f(x)\)
⏵Nếu bài toán yêu cầu tìm tham số để phương trình có \(k\) nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên để xác định sao cho đường thẳng \(y = f(m)\) nằm ngang cắt đồ thị hàm số \(y = f(x)\) tại \(k\) điểm phân biệt.
B. Bài tập minh họa tìm m để phương trình có nghiệm
Ví dụ 1. Với giá trị nào của tham số \(m\)thì phương trình \(x + \sqrt{4 - x^{2}} = m\) có nghiệm?
A. \(- 2 < m < 2\). B. \(- 2 < m < 2\sqrt{2}\).
C. \(- 2 \leq m \leq 2\sqrt{2}\). D. \(- 2 \leq m \leq 2\).
Hướng dẫn giải
Chọn C
Xét hàm số \(f(x) = x + \sqrt{4 -
x^{2}}\)trên \(\lbrack -
2;2\rbrack\)
Ta có: \(y' = 1 - \frac{x}{\sqrt{4 -
x^{2}}}\).
Cho \(y' = 0 \Leftrightarrow 1 -
\frac{x}{\sqrt{4 - x^{2}}} = 0 \Leftrightarrow \sqrt{4 - x^{2}} =
x\)
\(\Leftrightarrow \left\{ \begin{matrix}
x \geq 0 \\
4 - x^{2} = x^{2}
\end{matrix} \right.\ \Leftrightarrow x = \sqrt{2}\).
Hàm số liên tục trên đoạn \(\lbrack -
2;2\rbrack\)có \(f( - 2) = -
2\), \(f\left( \sqrt{2} \right) =
2\sqrt{2}\), \(f(2) = 2\).
Vậy \(\min_{\lbrack - 2;2\rbrack}f(x) = -
2\), \(\max_{\lbrack - 2;2\rbrack}f(x)
= 2\sqrt{2}\).
Do đó, phương trình \(x + \sqrt{4 - x^{2}}
= m\)có nghiệm khi \(- 2 \leq m \leq
2\sqrt{2}\).
Ví dụ 2. Tìm \(m\) để phương trình sau có nghiệm: \(\sqrt{3 + x} + \sqrt{6 - x} -
\sqrt{(3 + x)(6 - x)} = m.\)
A. \(0 \leq m \leq 6\). B. \(3 \leq m \leq 3\sqrt{2}\).
C. \(- \frac{1}{2} \leq m \leq
3\sqrt{2}\). D. \(3\sqrt{2} -
\frac{9}{2} \leq m \leq 3\).
Hướng dẫn giải
Chọn đáp án D.
Xét hàm số \(f(x) = \sqrt{3 + x} + \sqrt{6
- x} - \sqrt{(3 + x)(6 - x)}\) trên \(\lbrack - 3;6\rbrack.\)
\(f'(x) = \frac{1}{2\sqrt{3 + x}} -
\frac{1}{2\sqrt{6 - x}} + \frac{2x - 3}{2\sqrt{(3 + x)(6 -
x)}}\)
\(\Leftrightarrow \left\lbrack
\begin{matrix}
x = \frac{3}{2} \\
\sqrt{6 - x} + \sqrt{3 + x} = 1\ \ (*)
\end{matrix} \right.\)
Vậy \(x = \frac{3}{2}.\) Ta có bảng biến thiên:
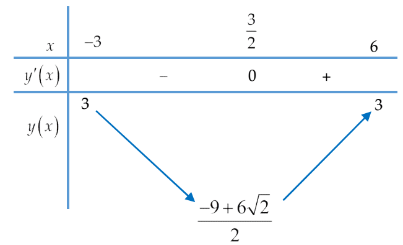
Vậy, để phương trình có nghiệm thì \(3\sqrt{2} - \frac{9}{2} \leq m \leq
3.\)
Ví dụ 3. Tìm \(m\) để phương trình \(x + 3 = m\sqrt{x^{2} + 1}\) có nghiệm.
A.\(1 \leq m \leq \sqrt{10}.\) B.\(- 1 \leq m \leq 10.\)
C.\(1 \leq m < \sqrt{10}.\) D.\(- 1 < m \leq \sqrt{10}.\)
Hướng dẫn giải
Chọn D
Ta có: \(x + 3 = m\sqrt{x^{2} +
1}\)\(\Leftrightarrow x + 3 = m\sqrt{x^{2} +
1}\)\(\Leftrightarrow \frac{x + 3}{\sqrt{x^{2}
+ 1}} = m.\)
Đặt \(f(x) = \frac{x + 3}{\sqrt{x^{2} +
1}}\). Phương trình có nghiệm khi đường thẳng \(y = m\) và đồ thị của hàm số \(y = f(x)\) có điểm chung.
Xét hàm số \(f(x) = \frac{x +
3}{\sqrt{x^{2} + 1}}\), \(x\mathbb{\in
R}\)
\(\lim_{x \rightarrow - \infty}f(x) = -
1\), \(\lim_{x \rightarrow +
\infty}f(x) = 1\)
\(f'(x) = \frac{1 - 3x}{\left(
\sqrt{x^{2} + 1} \right)^{3}}.\) Ta có \(f'(x) = 0 \Leftrightarrow x =
\frac{1}{3}\)
Bảng biến thiên:
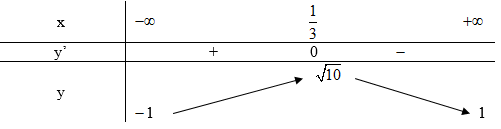
Để phương trình \(f(x) = m\) có nghiệm \(\Leftrightarrow - 1 < m \leq
\sqrt{10}.\)
Chọn đáp án D.
Ví dụ 4. Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\lbrack - 10;10\rbrack\) để phương trình \(\sqrt{2x^{2} - 3x + m} = x - 2\) có nghiệm?
Hướng dẫn giải
Xét phương trình \(\sqrt{2x^{2} - 3x + m} =
x - 2\) (*)
\((*) \Leftrightarrow \left\{
\begin{matrix}
x - 2 \geq 0 \\
2x^{2} - 3x + m = (x - 2)^{2}
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
x - 2 \geq 0 \\
m = - x^{2} - x + 4\ (**)\ \
\end{matrix} \right.\)
Phương trình (*) có nghiệm \(\Leftrightarrow\) Phương trình (**) có ít nhất một nghiệm thuộc \(\lbrack 2; +
\infty)\)
\(\Leftrightarrow\) Parabol \((P):y = - x^{2} - x + 4\)cắt đường thẳng \((d):y = m\) tại ít nhất một điểm có hoành độ thuộc \(\lbrack 2; +
\infty)\).
Ta có bảng biến thiên:
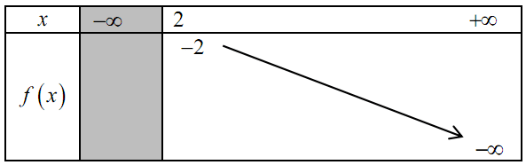
Từ bảng biến thiên, ta có \(m \leq -
2\).
Theo giả thiết \(m \in \lbrack -
10;10\rbrack\).
Do đó \(m \in \left\{ - 10; - 9; - 8; - 7;
- 6; - 5; - 4; - 3; - 2 \right\}\).
C. Bài tập vận dụng tự rèn luyện có đáp án hướng dẫn
Bài tập 1. Tìm \(m\) để phương trình sau có nghiệm:
\(\left( \sqrt{4 - x} + \sqrt{4
+ x} \right)^{3} - 6\sqrt{16 - x^{2}} + 2m + 1 = 0.\)
A. \(m\mathbb{\in R}.\) B. \(m > \frac{- 1 - 16\sqrt{2}}{2}.\) C. \(- \frac{41}{2} \leq m \leq \frac{- 1 -
16\sqrt{2}}{2}.\) D. \(m < -
\frac{41}{2}.\)
Bài tập 2. Phương trình \(3\sqrt{x - 1} +
m\sqrt{x + 1} = 2\sqrt[4]{x^{2} - 1}\) có nghiệm \(x\) khi:
A. \(0 \leq m \leq \frac{1}{3}\). B. \(- 1 < m \leq \frac{1}{3}\). C. \(m \leq \frac{1}{3}\). D. \(- 1 \leq m \leq \frac{1}{3}\).
Bài tập 3. Phương trình \(x^{3} + x(x + 1)
= m\left( x^{2} + 1 \right)^{2}\)có nghiệm thực khi và chỉ khi
A. \(- 6 \leq m \leq \frac{3}{4}\). B. \(- 1 \leq m \leq
\frac{14}{25}\). C. \(m \leq \frac{4}{3}\). D.\(- \frac{1}{4} \leq m \leq
\frac{3}{4}\).
Bài tập 4. Phương trình \(x^{3} + x(x + 1)
= m\left( x^{2} + 1 \right)^{2}\) có nghiệm thực khi và chỉ khi
A. \(- 6 \leq m \leq \frac{3}{4}\). B. \(- 1 \leq m \leq
\frac{14}{25}\). C. \(m \leq \frac{4}{3}\). D.\(- \frac{1}{4} \leq m \leq
\frac{3}{4}\).
Bài tập 5. Gọi \(S\) là tập tất cả các giá trị nguyên âm của tham số \(m\)để phương trình \(x + \sqrt{4 - x^{2}} = \frac{m}{2}\)có nghiệm. Tập \(S\)có bao nhiêu phần tử?
A. \(10\). B. \(6\). C. \(4\). D. \(2\).
Bài tập 6. Tìm tất cả các giá trị thực của tham số \(m\)sao cho phương trình \(2\sqrt{x + 1} = x + m\) có nghiệm thực?
A. \(m \leq 3\). B. \(m \leq 2\). C. \(m \geq 3\). D. \(m \geq 2\).
Bài tập 7. Biết rằng phương trình \(\sqrt{2
- x} + \sqrt{2 + x} - \sqrt{4 - x^{2}} = m\) có nghiệm khi \(m\) thuộc \(\lbrack a;b\rbrack\) với \(a\), \(b\mathbb{\in R}\). Khi đó giá trị của \(T = (a + 2)\sqrt{2} + b\) là
A. \(T = 3\sqrt{2} + 2\). B. \(T = 6\). C. \(T =
8\). D. \(T = 0\).
Bài tập 8. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\sqrt{1 + x} + \sqrt{8 - x} + \sqrt{8 + 7x -
x^{2}} = m\) có nghiệm thực?
A. \(13\). B. \(12\). C. \(6\). D. \(7\).
📘 Nội dung tài liệu còn tiếp tục, mời bạn tải bản đầy đủ để tham khảo chi tiết hơn.
---------------------------------------------------
Khi hiểu rõ bản chất tương giao của các đồ thị hàm số, việc tìm điều kiện của m để phương trình có nghiệm trở nên trực quan và hiệu quả hơn. Hy vọng những chia sẻ trong bài viết sẽ giúp bạn tự tin vận dụng kiến thức vào các bài toán Toán 12, đặc biệt là các câu hỏi tham số m trong đề thi THPT Quốc gia.
