Bài toán tối ưu diện tích trong thực tế
Cách giải bài toán tối ưu diện tích hình học
A. Bài tập minh họa tối ưu diện tích hình phẳng
Ví dụ 1. Người ta muốn làm một cánh diều hình quạt sao cho với chu vi cho trước là 
\(a\) sao cho diện tích của hình quạt lớn nhất. Dạng của quạt này phải như thế nào?
A. \(x = \frac{a}{4} ; y = \frac{a}{2}\) B. \(x\ \ = \ \
\frac{a}{3}\ \ ;\ \ y\ \ = \ \ \frac{a}{3}\)
C. \(x\ \ = \ \ \frac{a}{6}\ \ ;\ \ y\
\ = \ \ \frac{2a}{3}\) D. Đáp án khác
Hướng dẫn giải
Chọn A
Hình vẽ minh hoa:
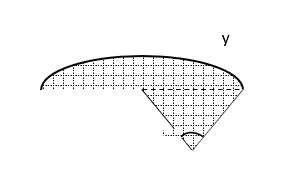
Gọi \(x\) là bán kính hình quạt, \(y\) là độ dài cung tròn. Ta có chu vi cánh diều là \(a = 2x + y\).
Ta cần tìm mối liên hệ giữa độ dài cung tròn y và bán kính \(x\) sao cho diện tích quạt lớn nhất.
Dựa vào công thức tính diện tích hình quạt là \(S = \frac{\pi\ R^{2\ }\alpha}{360}\)và độ dài cung tròn\(\mathcal{l\ \ = \ \
}\frac{2\pi R\alpha}{360}\), ta có diện tích hình quạt là: \(S\ = \ \frac{\mathcal{l\ }R}{2}\).
Vận dụng trong bài toán nàydiện tích cánh diều là: \(S\ \ = \ \frac{xy}{2}\ = \ \frac{x(a\ - \
2x)}{2}\ = \ \frac{1}{4}2x(a\ - \ 2x)\).
Dễ thấy\(S\) cực đại \(\Leftrightarrow 2x = a - 2x \Leftrightarrow \ \ x\
\ = \ \ \frac{a}{4}\ \ \Rightarrow \ \ y\ \ = \ \
\frac{a}{2}\).
Như vậy với chu vi cho trước, diện tích của hình quạt cực đại khi bán kính của nó bằng nửa độ dài cung tròn.
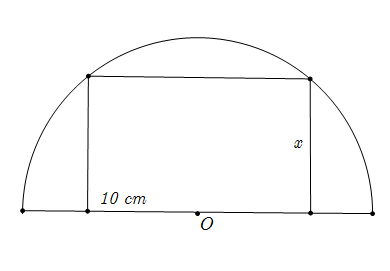
Ví dụ 2. Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính \(10cm\), biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn.
A. \(80cm^{2}\) B. \(100cm^{2}\) C. \(160cm^{2}\) D. \(200cm^{2}\)
Hướng dẫn giải
Chọn B.
Hình vẽ minh họa:
Gọi \(x(cm)\) là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn \((0 < x < 10)\).
Khi đó độ dài cạnh hình chữ nhật nằm dọc trên đường tròn là: \(2\sqrt{10^{2} - x^{2}}\ (cm)\)
Diện tích hình chữ nhật: \(S =
2x\sqrt{10^{2} - x^{2}}\ \left( cm^{2} \right)\)
Ta có \(S' = 2\sqrt{10^{2} - x^{2}} -
\frac{2x^{2}}{\sqrt{10^{2} - x^{2}}} = 2.10^{2} - 4x^{2}\)
\(S' = 0 \Leftrightarrow \left\lbrack
\begin{matrix}
x = \frac{10\sqrt{2}}{2}\ (tm) \\
x = - \frac{10\sqrt{2}}{2}\ (ktm)
\end{matrix} \right.\)
\(S'' = - 8x \Rightarrow
S''\left( \frac{10\sqrt{2}}{2} \right) = - 40\sqrt{2} <
0\). Suy ra \(x =
\frac{10\sqrt{2}}{2}\) là điểm cực đại của hàm \(S(x)\).
Vậy diện tích lớn nhất của hình chữ nhật là: \(S = 10\sqrt{2}.\sqrt{10^{2} - \frac{10^{2}}{2}} =
100\left( cm^{2} \right)\)
Ví dụ 3. Trong các tam giác vuông có tổng của một cạnh góc vuông và cạnh huyền là \(a;(a > 0)\), tam giác có diện tích lớn nhất là
A. \(\frac{a^{2}}{5\sqrt{6}}\). B. \(\frac{a^{2}}{3\sqrt{6}}\). C. \(\frac{a^{2}}{6\sqrt{5}}\). D. \(\frac{a^{2}}{6\sqrt{3}}\).
Hướng dẫn giải
Chọn D
Giả sử \(\Delta ABC\)vuông tại \(A\) và có \(AB +
BC = a\).
Đặt \(AB = x \Rightarrow BC = a -
x\). Vì \(BC > AB \Rightarrow 0 <
x < \frac{a}{2}\) nên ta có: \(AC =
\sqrt{BC^{2} - AB^{2}} = \sqrt{(a - x)^{2} - x^{2}} = \sqrt{a^{2} -
2ax}\).
Diện tích tam giác \(ABC\)là \(S = \frac{1}{2}AB.AC = \frac{1}{2}x.\sqrt{a^{2} -
2ax} = \frac{1}{2}\sqrt{a^{2}x^{2} - 2ax^{3}}\).
Xét hàm số \(y = a^{2}x^{2} - 2ax^{3},0
< x < \frac{a}{2}\) ta có: \(y' = 2a^{2}x - 6ax\)
Xét \(y' = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = \frac{a}{3}
\end{matrix} \right.\)
Bảng biến thiên:
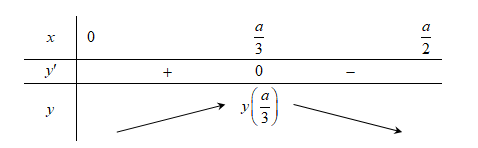
Nhìn vào bảng biến thiên suy ra tam giác có diện tích lớn nhất là \(\frac{a^{2}}{6\sqrt{3}}\) khi \(x = \frac{a}{3}\).
C. Bài tập vận dụng có hướng dẫn giải chi tiết
Bài tập 1. Một lão nông chia đất cho con trai để người con canh tác riêng, biết người con sẽ được chọn miếng đất hình chữ nhật có chu vi bằng \(800(m)\). Hỏi anh ta chọn mỗi kích thước của nó bằng bao nhiêu để diện tích canh tác lớn nhất?
Bài tập 2. Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là \(180\) mét thẳng hàng rào. Ở đó người ta tận dụng một bờ giậu có sẵn để làm một cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Hỏi mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu?
A. \(S_{\max} = 3600m^{2}\) B. \(S_{\max} = 4000m^{2}\)
C. \(S_{\max} = 8100m^{2}\) D. \(S_{\max} = 4050m^{2}\)
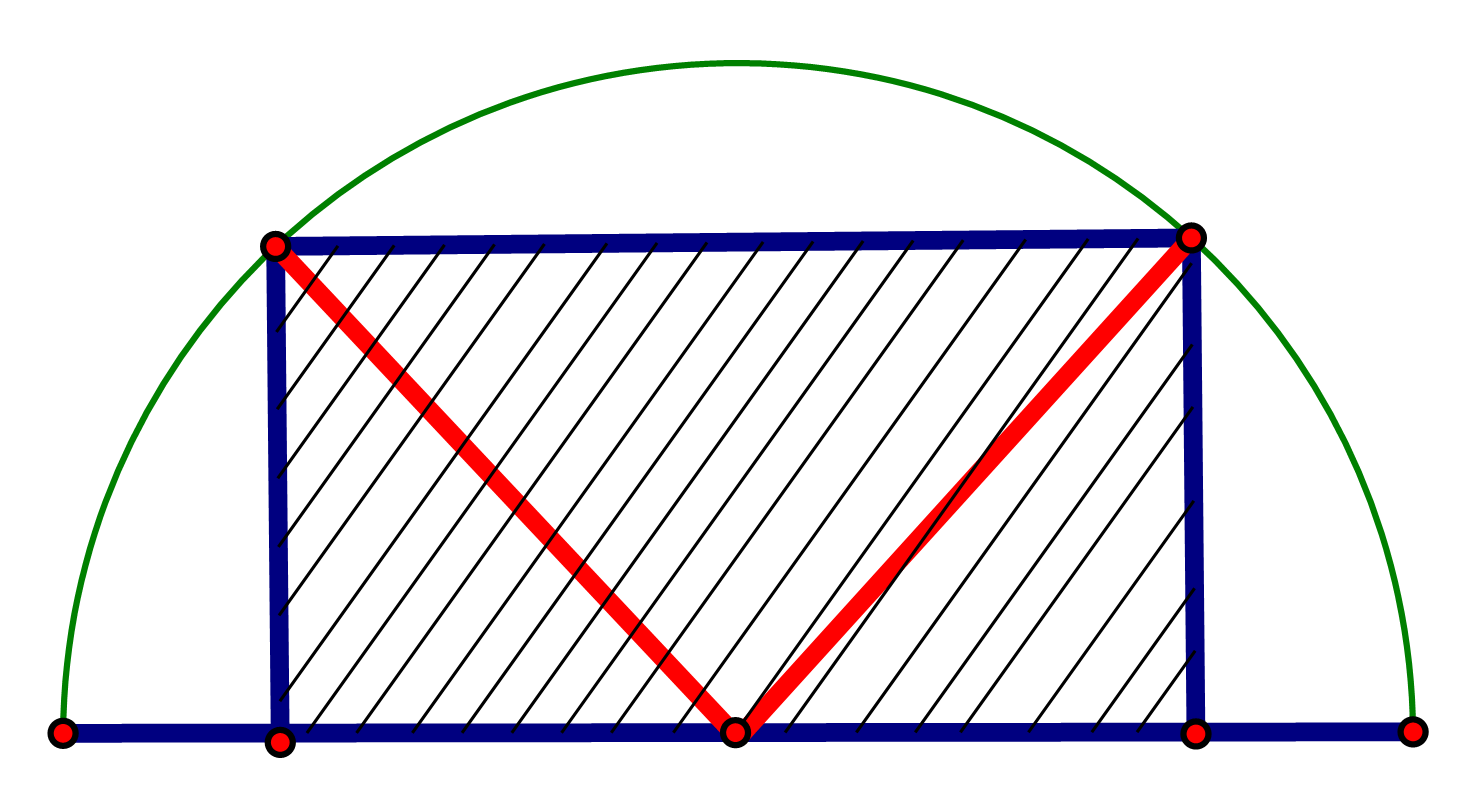
Bài tập 3. Tính diện tích lớn nhất \(S_{\max}\) của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính \(R = 6\
cm\) nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp.
A. \(S_{\max} = 36\pi\ cm^{2}\). B.\(S_{\max} = 36\ cm^{2}\).
C.\(S_{\max} = 96\pi\ cm^{2}\). D.\(S_{\max} = 18\ \ cm^{2}\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu!
-----------------------------------------------------
Có thể thấy, bài toán tối ưu diện tích trong thực tế là dạng toán vừa mang tính ứng dụng cao, vừa giúp học sinh hiểu sâu bản chất của đạo hàm trong việc tìm GTLN – GTNN. Việc thành thạo các bước lập hàm số, khảo sát và kết luận không chỉ hỗ trợ tốt cho quá trình ôn thi mà còn rèn luyện tư duy giải quyết vấn đề một cách logic và hiệu quả.
Hy vọng bài viết đã cung cấp cho bạn hệ thống kiến thức đầy đủ, dễ hiểu và có tính ứng dụng cao. Đừng quên luyện tập thêm nhiều dạng bài tương tự để tự tin chinh phục mọi dạng bài tập ôn thi THPT Quốc gia ứng dụng trong thực tiễn.
