Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Chuyên đề Toán 12 Tọa độ của Vectơ trong không gian ứng dụng thực tế

Ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Ứng dụng thực tế Tọa độ của vectơ trong không gian

A. Đề bài trắc nghiệm bài tập ứng dụng thực tế tọa độ vectơ trong không gian
B. Đáp án tổng quan bài tập trắc nghiệm
C. Hướng dẫn giải chi tiết bài tập trắc nghiệm

Trong chương trình Toán 12, phần tọa độ của vectơ trong không gian là một trong những kiến thức quan trọng giúp học sinh giải quyết các bài toán hình học không gian phức tạp. Việc nắm vững lý thuyết và phương pháp tính toán về tọa độ của vectơ không chỉ hỗ trợ bạn trong việc giải bài tập mà còn giúp bạn ứng dụng kiến thức vào các tình huống thực tế. Ôn thi THPT Quốc gia môn Toán cũng sẽ không thiếu các câu hỏi liên quan đến vectơ trong không gian, đặc biệt là các bài toán về tính toán tọa độ của vectơ trong không gian ba chiều.

Bài viết này sẽ giúp bạn hiểu rõ về tọa độ vectơ, từ đó nắm bắt được các phương pháp giải bài toán Toán 12 có liên quan, giúp bạn tự tin hơn trong kỳ thi THPT Quốc gia sắp tới.

A. Đề bài trắc nghiệm bài tập ứng dụng thực tế tọa độ vectơ trong không gian

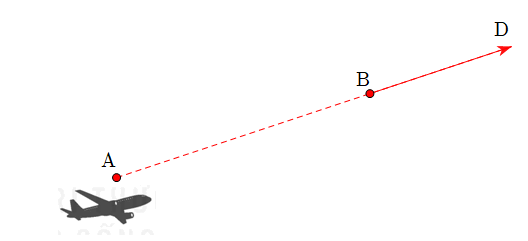
Câu 1: Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo D(x; y; z). Khi đó x + y + z = ?

A. 1689. B. 1307. C. 1498. D. 925.

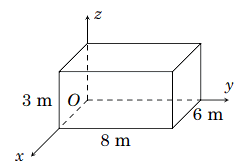
Câu 2: Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục toạ độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét. Hãy tìm toạ độ của điểm treo đèn?

A. $\left( \frac{3}{2}\ ;\ 4\ ;\ 0 \right)$ B. (3; 4; 3). C. (3; 4; 0). D. (3; 0; 4).

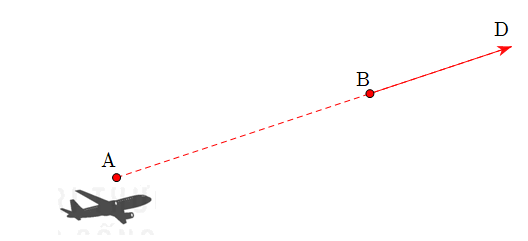
Câu 3: Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là gì?

A. (1245; 2056; 735). B. (1 010; 575; 8,5).

C. (105; 2965; 10). D. (1 010; 575; 8).

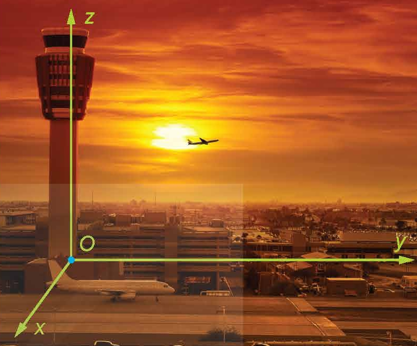
Câu 4: Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ toạ độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng (Oxy) trùng với mặt đất với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời. Sau khi cất cánh và đạt độ cao nhất định, chiếc máy bay duy trì hướng bay về phía nam với tốc độ không đổi là 890km/h trong nửa giờ. Xác định toạ độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó đối với hệ toạ độ đã chọn, biết rằng đơn vị đo trong không gian Oxyz được lấy theo kilômét.

A. (0; 435; 0). B. (0; 445; 0). C. (445; 0; 0). D. (435; 0; 0).

Câu 5: Máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm M(600; 400; 20) đến điểm N(800; 500; 30) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 15 phút tiếp theo bằng bao nhiêu?

A. (700; 500; 30). B. (900; 650; 55).

C. (900; 550; 35). D. (800; 540; 30).

Câu 6: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{a} = \left( 2;\frac{1}{3}; - 5 \right)$ và điểm M(2;3;4). Tọa độ điểm N thỏa mãn $\overrightarrow{MN} = \overrightarrow{a}$ là:

A. $\left( 2;\frac{5}{3}; - \frac{1}{2} \right)$ B. $\left( 0;\frac{8}{3};9 \right)$ C. $\left( 4;\frac{10}{3}; - 1 \right)$ D. $\left( 0; - \frac{8}{3}; - 9 \right)$

Câu 7: Nếu một vật có khối lượng m (kg) thì lực hấp dẫn $\overrightarrow{P}$ của trái đất tác dụng lên vật được xác định theo công thức $\overrightarrow{p} = m\ \overrightarrow{g}$ , trong đó $\overrightarrow{g}$ là gia tốc rơi tự do có độ lớn g = 9,8 (m/s²). Độ lớn của lực Trái Đất tác dụng lên một quả lê có khối lượng 105g là:

A. 102,9 N. B. 1029 N. C. 1,029N. D. 10,29N.

Câu 8: Cho biết máy bay A đang bay với vận tốc $\overrightarrow{u} = (300;200;400)$ ( đơn vị:km/h)

Máy bay B ngược hướng và có tốc độ gấp 2 lần tốc độ của máy bay A. Tọa độ vectơ vận tốc $\overrightarrow{v}$ của máy bay B là:

A. $\overrightarrow{v} = (600;400;800)$ B. $\overrightarrow{v} = (150;100;200)$

C. $\overrightarrow{v} = ( - 600; - 400; - 800)$ D. $\overrightarrow{v} = ( - 150; - 100; - 200)$

Câu 9: Trong không gian Oxyz cho ba điểm A(3; 5; -1), B(7; x; 1) và C(9; 2; y). Để A; B; C thẳng hàng thì giá trị x + y bằng:

A. 5 B. 6 C. 4 D. 7

Câu 10: Trong không gian Oxyz điểm M thuộc trục Ox và cách đều hai điểm A(4; 2; -1) và B(2; 1; 0) là:

A. M(-4; 0; 0). B. M(5; 0; 0). C. M(4; 0; 0). D. M(-5; 0; 0).

Câu 11: Trong không gian với hệ toạ độ Oxyz, cho điểm M(4; 1; -2) và vectơ $\overrightarrow{u} = (4; - 2;6).$ Tìm toạ độ điểm N biết rằng $\overrightarrow{MN} = - \frac{1}{2}\overrightarrow{u}$ .

A. (3; 1; 2). B. (-1; 5; 3). C. (-3; 3; 3). D. (2; 2; -5).

Câu 12: Trong không gian Oxyz, cho $\overrightarrow{a} = (2; - 2;1)$ và $\ \overrightarrow{b} = (x - 1)\overrightarrow{i} + \left( x^{2} - 3 \right)\overrightarrow{j} + y\overrightarrow{j}$ . Khi $\overrightarrow{a} = \overrightarrow{b}$ thì giá trị x - y bằng?

A. 0 B. 2 C. 1 D. -1

Câu 13: Trong không gian Oxyz, cho A(1; 0; 0), B(0; 2; 0); M(x - 1; 2y - 2; 7). Gọi M' là hình chiếu của M trên mặt phẳng (Oxy). Khi tứ giác OBM'A là hình bình hành thì giá trị x +y bằng?

A. 4 B. 2 C. 1 D. -1

Câu 14: Trong không gian Oxyz cho hình hộp chữ nhật OABC.EFGH có các cạnh OA = 5, OC = 8, OE = 7 (xem hình vẽ dưới đây).

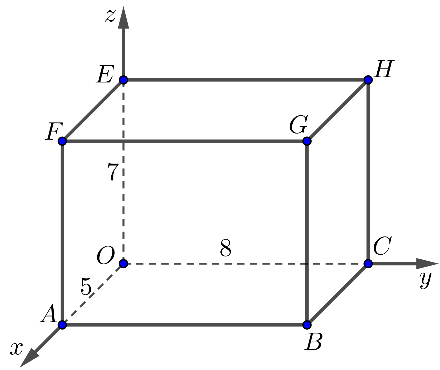
Tọa độ H(x; y; z). Tính giá trị biểu thức: P = 50X + 75Y + 1000Z?

A. 7600 B. 6580 C. 7134 D. 6783

Câu 15: Trong không gian Oxyz, cho A(3; 2; -1), B(-1; 0; 5). Điểm M(a; b; c) thay đổi thuộc mặt phẳng (Oxy). Tính giá trị của biểu thức T = a + b + c khi $\left| \overrightarrow{MA} + \overrightarrow{MB} \right|$ nhỏ nhất.

A. 2 B. 7 C. 5 D. 10

Câu 16: Trong không gian Oxyz cho A(1; 0; 2), B(-1; 2; 2), C(3; 1; 1). Gọi M(a; b; c) là điểm thuộc mặt phẳng (Oxz) sao cho biểu thức $S = 2\overrightarrow{MA}.\overrightarrow{MB} + \overrightarrow{MB}.\overrightarrow{MC} + 3\overrightarrow{MC}.\overrightarrow{MA}$ đạt giá trị nhỏ nhất. Khi đó T = 6a - 5b + 3c có giá trị là:

A. 12 B. 25 C. 16 D. 23

Câu 17: Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5 , giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ $\overrightarrow{OB},\ \ \overrightarrow{OC},\ \ \overrightarrow{OS}$ lần lượt cùng hướng với $\overrightarrow{i}$ , $\overrightarrow{j},\overrightarrow{k}$ và OA = OS = M như hình bên dưới.

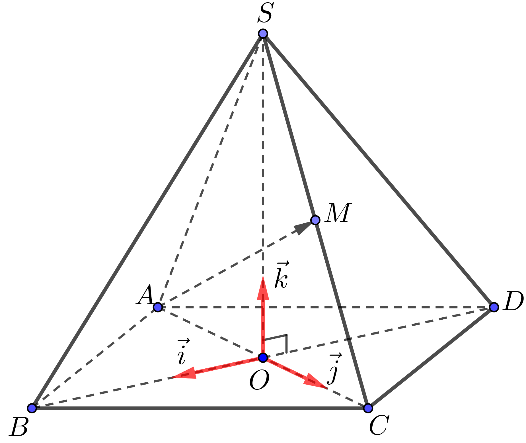
Toạ độ vectơ $\overrightarrow{AM} = (a;b;c)$ với M là trung điểm của cạnh SC, khi đó a +b +c bằng bao nhiêu?

A. 8 B. -1 C. 0 D. -5

B. Đáp án tổng quan bài tập trắc nghiệm

1 - A	2 - B	3 - B	4 – B	5 - C	6 - C	7 – B
8 - C	9 - A	10 - C	11 - D	12 - A	13 - A	14 – A
15 - A	16 - A	17 - A	18 - D	19 - A	20 - B	21 - C

C. Hướng dẫn giải chi tiết bài tập trắc nghiệm

Câu 1:

Gọi là vị trí của máy bay sau 10 phút bay tiếp theo. Vì hướng của máy bay không đổi nên $\overrightarrow{AB}$ và $\overrightarrow{BD}$ cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ đến bằng thời gian bay từ B đến D nên AB = BD.

Do đó, $\overrightarrow{BD} = \overrightarrow{AB} = (140;50;1)$ .

Mặt khác: $\overrightarrow{BD} = (x - 940;y - 550;z - 8)$ nên $\left\{ \begin{matrix} x - 940 = 140 \\ y - 550 = 50 \\ z - 8 = 1 \end{matrix} \Leftrightarrow \left\{ \begin{matrix} x = 1080 \\ y = 600 \\ z = 9 \end{matrix} \right.\ \right.$

Vậy D(1080; 600; 9). Vậy tọa độ của máy bay trong 10 phút tiếp theo là (1080; 600; 9).

Suy ra x + y + z = 1689.

Câu 2:

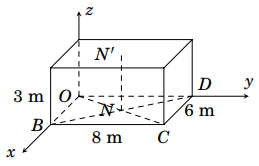
Gọi toạ độ các điểm B(6;0;0), C(6; 8; 0), D(0; 8; 0) như hình vẽ dưới đây:

Gọi N là trung điểm của OC, N' là hình chiếu của N lên mặt phẳng trần nhà suy ra N' là điểm treo đèn.

Khi đó N(3;4;0) => N'(3; 4; 3)

Vậy toạ độ của điểm treo đèn là (3; 4; 3).

Câu 3:

Gọi D(x; y; z) là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên $\overrightarrow{AB}$ và $\overrightarrow{BD}$ cùng hướng. Do vận tốc của máy bay không đổi và thời gian bay từ A đến B gấp đôi thời gian bay từ B đến D nên AB = 2BD.

Do đó $\overrightarrow{BD} = \frac{1}{2}\overrightarrow{AB} = (70;25;0,5)$ .

Mặt khác, $\overrightarrow{BD} = (x - 940;y - 550;z - 8)$ nên:

$\left\{ \begin{matrix} x - 940 = 70 \\ y - 550 = 25 \\ z - 8 = 0,5 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 1010 \\ y = 575 \\ z = 8,5 \end{matrix} \right.\ \Rightarrow D(1010;575;8,5)$ .

Vậy tọa độ của máy bay sau 5 phút tiếp theo là (1 010; 575; 8,5).

Câu 4:

Quãng đường máy bay bay được với vận tốc 890km/h trong nửa giờ là:

890 : 2 = 445 (km).

Vì máy bay duy trì hướng bay về phía nam nên tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó với hệ tọa độ đã chọn là (0; 445; 0)

Câu 5:

Gọi Q(x; y; z) là tọa độ của máy bay sau 15 phút tiếp theo.

$\overrightarrow{MN} = (200;100;10)$

$\overrightarrow{NQ} = (x - 800;y - 500;z - 30)$

Vì máy bay giữ nguyên hướng bay nên $\overrightarrow{MN}$ và $\overrightarrow{NQ}$ cùng hướng.

Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ M-> N gấp 2 lần thời gian bay từ N -> Q nên MN = 2NQ.

Suy ra

$\overrightarrow{MN} =2\overrightarrow{NQ} \Leftrightarrow \left\{ \begin{matrix}200 = 2(x - 800) \\100 = 2(y - 500) \\10 = 2(z - 30)\end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix}x = 900 \\y = 550 \\z = 35\end{matrix} \right.\ \Rightarrow Q(900;550;35)$

Tọa độ của máy bay sau 15 phút tiếp theo là (900; 550; 35).

Câu 6:

Gọi tọa độ điểm N là $\left( x_{N};y_{N};z_{N} \right)$ , ta có: $\overrightarrow{MN} = \left( x_{N} - 2;y_{N} - 3;z_{N} - 4 \right)$ .

Ta có:

$\overrightarrow{MN} = \overrightarrow{a} \Leftrightarrow \left\{ \begin{matrix} x_{N} - 2 = 2 \\ y_{N} - 3 = \frac{1}{3} \\ z_{N} - 4 = - 5 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x_{N} = 2 + 2 \\ y_{N} = \frac{1}{3} + 3 \\ z_{N} = - 5 + 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{N} = 4 \\ y_{N} = \frac{10}{3} \\ z_{N} = - 1 \end{matrix} \right.$ .

Vậy $N\left( 4;\frac{10}{3}; - 1 \right)$ _.

Câu 7:

Đổi 105g = 0,105kg

Độ lớn của lực hấp dẫn của trái đất tác dụng lên quả lê là:

$\left| \overrightarrow{p} \right| = m\left| \overrightarrow{g} \right| = 0,105.9,8 = 1,029N.$

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

--------------------------------------------------------

Qua bài viết này, hy vọng bạn đã có cái nhìn rõ hơn về tọa độ vectơ trong không gian và các ứng dụng thực tế của chúng trong bài toán hình học không gian lớp 12. Việc nắm vững những kiến thức này sẽ giúp bạn không chỉ đạt kết quả cao trong kỳ thi THPT Quốc gia môn Toán mà còn tạo nền tảng vững chắc cho việc học các môn toán cao cấp sau này. Đừng quên ôn tập và luyện tập thường xuyên để cải thiện kỹ năng giải quyết bài toán một cách nhanh chóng và chính xác! Chúc bạn ôn thi hiệu quả và đạt kết quả tốt trong kỳ thi THPT Quốc gia!

Tải về

Chọn file muốn tải về: