Chuyên đề Toán 12 Ứng dụng hình học Tích phân tính thể tích
Tính thể tích vật thể giới hạn bởi đồ thị hàm số
Trong chương trình Toán 12, phần ứng dụng hình học của tích phân để tính thể tích là một nội dung quan trọng, giúp học sinh hiểu rõ mối liên hệ giữa giải tích và hình học không gian. Đây là dạng toán thường xuất hiện trong đề thi THPT quốc gia môn Toán, đòi hỏi học sinh nắm vững công thức, kỹ năng thiết lập tích phân và phương pháp tính nhanh. Bài viết này sẽ hệ thống kiến thức lý thuyết, phân loại dạng toán và đưa ra ví dụ minh họa, giúp bạn rèn luyện hiệu quả và đạt điểm số cao.
A. Đề bài trắc nghiệm Ứng dụng hình học Tích phân tính thể tích
Câu 1: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x ![]() thì được thiết diện là một hình chữ nhật có hai cạnh là 3x và x2.
thì được thiết diện là một hình chữ nhật có hai cạnh là 3x và x2.
A. V = 60 B. V = 54 C. V = 71 D. V = 63
Câu 2: Tính thể tích ![]() của vật thể nằm giữa hai mặt phẳng x = 0 và
của vật thể nằm giữa hai mặt phẳng x = 0 và ![]() , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục
, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục ![]() tại điểm có hoành độ x
tại điểm có hoành độ x ![]() là một tam giác đều cạnh
là một tam giác đều cạnh ![]() .
.
A. V = 2 B. ![]() C.
C. ![]() D.
D. ![]()
Câu 3: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường ![]() , trục Ox và hai đường thẳng x = 1;x = 4 khi quay quanh trục hoành được tính bởi công thức nào?
, trục Ox và hai đường thẳng x = 1;x = 4 khi quay quanh trục hoành được tính bởi công thức nào?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 4: Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox : ![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 5: Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ![]() , mặt cắt là tam giác vuông có một góc 450 và độ dài một cạnh góc vuông là
, mặt cắt là tam giác vuông có một góc 450 và độ dài một cạnh góc vuông là ![]() (như hình vẽ).
(như hình vẽ).
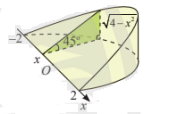
Tính thể tích vật thể hình chiếc niêm trên.
A. V = 20 B. V = 25 C. V = 35 D. V = 30
Câu 6: Trong chương trình nông thôn mới của tỉnh Phú Yên, tại xã Hòa Mỹ Tây có xây một cây cầu bằng bê tông như hình vẽ (đường cong trong hình vẽ là các đường Parabol).
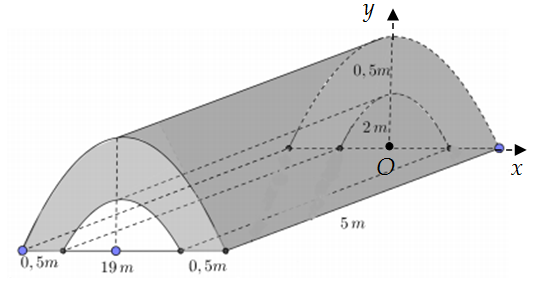
Biết 1m3 khối bê tông để đổ cây cầu có giá 5 triệu đồng. Tính số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu trên.
A. 42m3 B. 40m3 C. 45m3 D. 47m3
Câu 7: Để kỷ niệm ngày 26-3. Chi đoàn 12A dự định dựng một lều trại có dạng parabol, với kích thước: nền trại là một hình chữ nhật có chiều rộng là ![]() mét, chiều sâu là
mét, chiều sâu là ![]() mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích phần không gian phía bên trong trại để lớp 12A cử số lượng người tham dự trại cho phù hợp.
mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích phần không gian phía bên trong trại để lớp 12A cử số lượng người tham dự trại cho phù hợp.
A. V = 36 B. V = 38 C. V = 32 D. V = 33
Câu 8: Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng ![]() . Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc 300 ta thu được hai khối gỗ có thể tích là V1 và V2, với
. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc 300 ta thu được hai khối gỗ có thể tích là V1 và V2, với ![]() . Tính thể tích V1.
. Tính thể tích V1.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 9: Cho một mô hình 3D mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài 5(cm); khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức![]()
![]() , với x(cm) là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình.
, với x(cm) là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình.
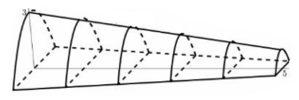
Tính thể tích (theo đơn vị cm3) không gian bên trong đường hầm mô hình (làm tròn kết quả đến hàng đơn vị).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 10: Một học sinh làm mô hình chiếc lều vải mini có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc lều như hình vẽ bên dưới.
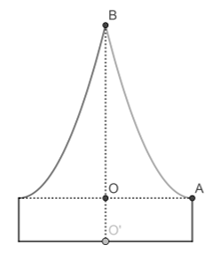
Biết rằng OO' = 5cm, OA = 10cm, OB = 20cm, đường cong AB là một phần của parabol có đỉnh là điểm A. Tính thể tích của chiếc lều.
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 11: Một chi tiết máy được thiết kế như hình vẽ bên.
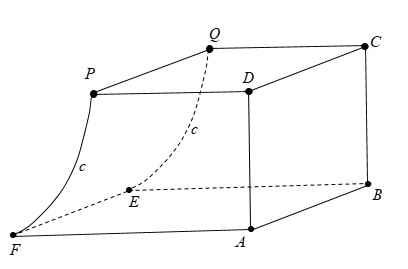
Các tứ giác ABCD, CDPQ là các hình vuông cạnh 2,5cm. Tứ giác ![]() là hình chữ nhật có BE = 3,5cm. Mặt bên PQEF được mài nhẵn theo đường parabol (P) có đỉnh parabol nằm trên cạnh EF. Tính thể tích của chi tiết máy gần nhất với giá trị nào dưới đây?
là hình chữ nhật có BE = 3,5cm. Mặt bên PQEF được mài nhẵn theo đường parabol (P) có đỉnh parabol nằm trên cạnh EF. Tính thể tích của chi tiết máy gần nhất với giá trị nào dưới đây?
A. 17cm3 B. 18cm3 C. 19cm3 D. 20cm3
Câu 12: Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 28cm, trục nhỏ 25cm. Biết cứ 1000cm3 dưa hấu sẽ làm được cốc sinh tố giá 20 000 đồng. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
A. 183 259 đồng B. 152 348 đồng
C. 167 584 đồng D. 177 946 đồng
Câu 13: Một ly rượu thủy tinh có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của ly (bổ dọc cốc thành 2 phần bằng nhau) là một đường Parabol. Tính thể tích tối đa mà ly có thể chứa được (làm tròn 2 chữ số thập phân).
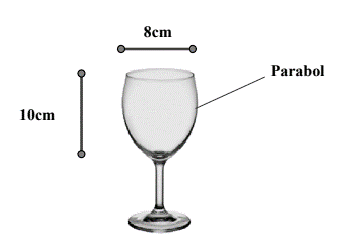
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 14: Gọi (H) là phần giao của hai khối ![]() hình trụ có bán kính a, hai trục hình trụ vuông góc với nhau như hình vẽ sau. Tính thể tích của khối (H).
hình trụ có bán kính a, hai trục hình trụ vuông góc với nhau như hình vẽ sau. Tính thể tích của khối (H).
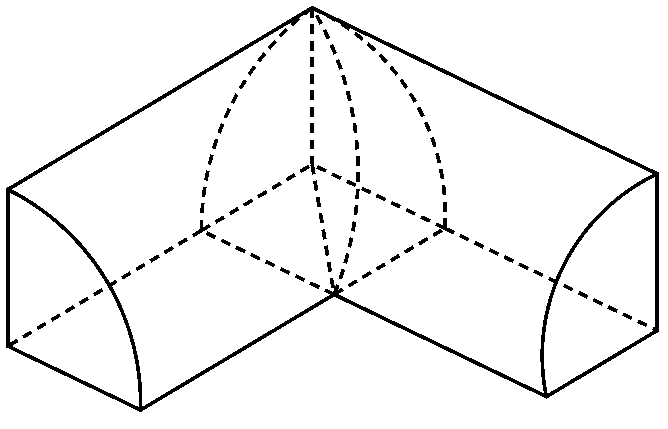
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 15: Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho h'(t) = 6at2 + 2bt và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là 90m3, sau 6 giây thì thể tích nước trong bể là 504m3. Tính thể tích nước trong bể sau khi bơm được 9 giây.
A. 1548(m3) B. 1854(m3) C. 1584(m3) D. 1458(m3)
B. Đáp án tổng quan bài tập trắc nghiệm
|
1 - A |
2 - B |
3 - A |
4 - A |
5 - A |
6 – B |
|
7 - A |
8 - C |
9 - A |
10 - A |
11 - B |
12 – A |
|
13 - B |
14 - C |
15 - D |
16 - A |
17 - C |
18 – A |
|
19 - C |
20 - C |
21 - B |
22 - A |
23 - C |
|
C. Hướng dẫn giải chi tiết bài tập trắc nghiệm
Câu 1:
Ta có diện tích thiết diện: S(x) = 3x.x2 = 3x3.
Khi đó ![]() .
.
Câu 2:
Ta có diện tích thiết diện: ![]() .
.
Thể tích cần tìm là: ![]() .
.
Câu 3:
Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số ![]() , trục Ox, x = 1 và x = 4 được tính bởi công thức
, trục Ox, x = 1 và x = 4 được tính bởi công thức
![]() .
.
Câu 4:
Thể tích khối tròn xoay ![]()
![]() .
.
Câu 5:
Diện tích tam giác vuông cân là:
![]()
![]() Thể tích vật thể là:
Thể tích vật thể là: ![]() .
.
Câu 6:
Chọn hệ trục Oxy như hình vẽ.
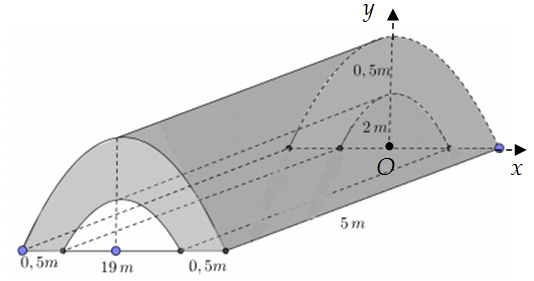
Gọi ![]() là Parabol đi qua hai điểm
là Parabol đi qua hai điểm ![]()
Nên ta có hệ phương trình sau: 

![]() .
.
Gọi ![]() là Parabol đi qua hai điểm
là Parabol đi qua hai điểm ![]()
Nên ta có hệ phương trình sau: 
![]() .
.
Ta có thể tích của bê tông là:  .
.
Số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu là: 5.40 = 200 triệu đồng.
🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.
-----------------------------------------------------------------------
Gợi ý tham khảo:
- Bài toán thực tế tối ưu Quãng đường – Phương pháp giải chuẩn nhất
- Chuyên đề Tìm tham số m để hàm số có cực trị
- Bài toán thực tế Ứng dụng Nguyên hàm, Tích phân Có đáp án chi tiết
- Chuyên đề Toán 12 Ứng dụng hình học Tích phân tính thể tích
- Bộ bài tập tìm m để bất phương trình nghiệm đúng với mọi x (Có lời giải)
- Bài tập Tìm m để hàm số đồng biến nghịch biến trên khoảng
- Chuyên đề Xét sự đồng biến, nghịch biến của hàm hợp, hàm ẩn
- Bộ Bài Tập Thực Tế Tìm GTLN – GTNN (Có Đáp Án & Giải Thích Chi Tiết)
- Tìm m để phương trình hàm hợp, hàm ẩn chứa tham số có n nghiệm
Có thể thấy rằng, chuyên đề Toán 12 ứng dụng hình học tích phân tính thể tích không chỉ giúp học sinh vận dụng thành thạo công cụ giải tích mà còn phát triển kỹ năng tư duy không gian, tính toán logic và chính xác. Đây là dạng toán quan trọng, thường gắn liền với việc tính thể tích khối tròn xoay, thể tích hình giới hạn bởi đồ thị hàm số và các miền phẳng đặc biệt.
Hy vọng nội dung trên đã mang đến cho bạn tài liệu học tập bổ ích, giúp hệ thống hóa công thức, phương pháp và các dạng bài tập cơ bản lẫn nâng cao. Để đạt hiệu quả tối ưu trong quá trình ôn thi THPT quốc gia môn Toán, bạn nên thường xuyên luyện đề, kết hợp tự luận và trắc nghiệm, đồng thời rèn luyện khả năng trình bày ngắn gọn, chính xác để tăng tốc độ làm bài và tự tin đạt điểm cao.










