Tổng hợp bài toán thực tế về tối ưu chi phí Toán 12
Bài toán thực tế tối ưu chi phí từ cơ bản đến nâng cao
Bài viết Tổng hợp bài toán thực tế về tối ưu chi phí Toán 12 mang đến hệ thống bài tập được chọn lọc kỹ lưỡng, sắp xếp từ mức độ cơ bản đến nâng cao, giúp người học từng bước nắm vững phương pháp giải và chủ động chinh phục các dạng toán thường gặp trong đề thi THPT Quốc gia môn Toán.
A. Bài tập minh họa tính tối ưu chi phí
Ví dụ 1. Anh Hùng muốn xây dựng một hố ga không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được 
\(3200cm^{3}\), tỉ số giữa chiều cao và chiều rộng của hố ga bằng \(2\). Xác định diện tích đáy của hố ga để khi xây hố tiết kiệm được nguyên vật liệu nhất.
A. \(170cm^{2}\). B. \(160cm^{2}\). C. \(150cm^{2}\). D. \(140cm^{2}\).
Hướng dẫn giải
Chọn B
Gọi \(a;b;h\) lần lượt là chiều dài, chiều rộng, chiều cao của hố ga.
Ta có hình vẽ:
Ta có:
\(\left\{ \begin{matrix}
abh = 3200 \\
\frac{h}{b} = 2
\end{matrix} \right.\)\(\Leftrightarrow \left\{ \begin{matrix}
2ab^{2} = 3200 \\
h = 2b
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
a = \frac{1600}{b^{2}} \\
h = 2b
\end{matrix} \right.\)
Để xây hố tiết kiệm nguyên vật liệu nhất thì \(S_{xq} + S_{đ}\)đạt giá trị nhỏ nhất.
\(S_{xq} + S_{đ} = 2bh + 2ah +
ab\)
\(= 4b^{2} + \frac{6400}{b} +
\frac{1600}{b} = 4b^{2} + \frac{8000}{b} = f(b)\)
Xét \(f(b) = 4b^{2} +
\frac{8000}{b}\)trên \((0; +
\infty)\)
\(f^{'(b)} = 8b - \frac{8000}{b^{2}}
\Rightarrow f^{'(b)} = 0\)\(\Leftrightarrow 8b^{3} - 8000 = 0
\Leftrightarrow b = 10\)
Bảng biến thiên:
Với \(b = 10 \Rightarrow a =
16\)
Vậy diện tích đáy hố ga để khi xây hố tiết kiệm được nguyên liệu nhất là: \(S_{đ} = 16.10 = 160\left( cm^{2}
\right)\).
Ví dụ 2. Đường dây điện \(110KV\) kéo từ trạm phát (điểm \(A\)) trong đất liền ra Côn Đảo (điểm \(C\)). biết khoảng cách ngắn nhất từ \(C\) đến \(B\) là \(60km\), khoảng cách từ \(A\) đến \(B\) là \(100km\), mỗi \(km\) dây điện dưới nước chi phí là \(5000USD\), chi phí cho mỗi \(km\) dây điện trên bờ là \(3000USD\). Hỏi điểm \(G\) cách \(A\) bao nhiêu để mắc dây điện từ \(A\) đến \(G\) rồi từ \(G\) đến \(C\) chi phí ít nhất.
Hướng dẫn giải
Hình vẽ minh họa:
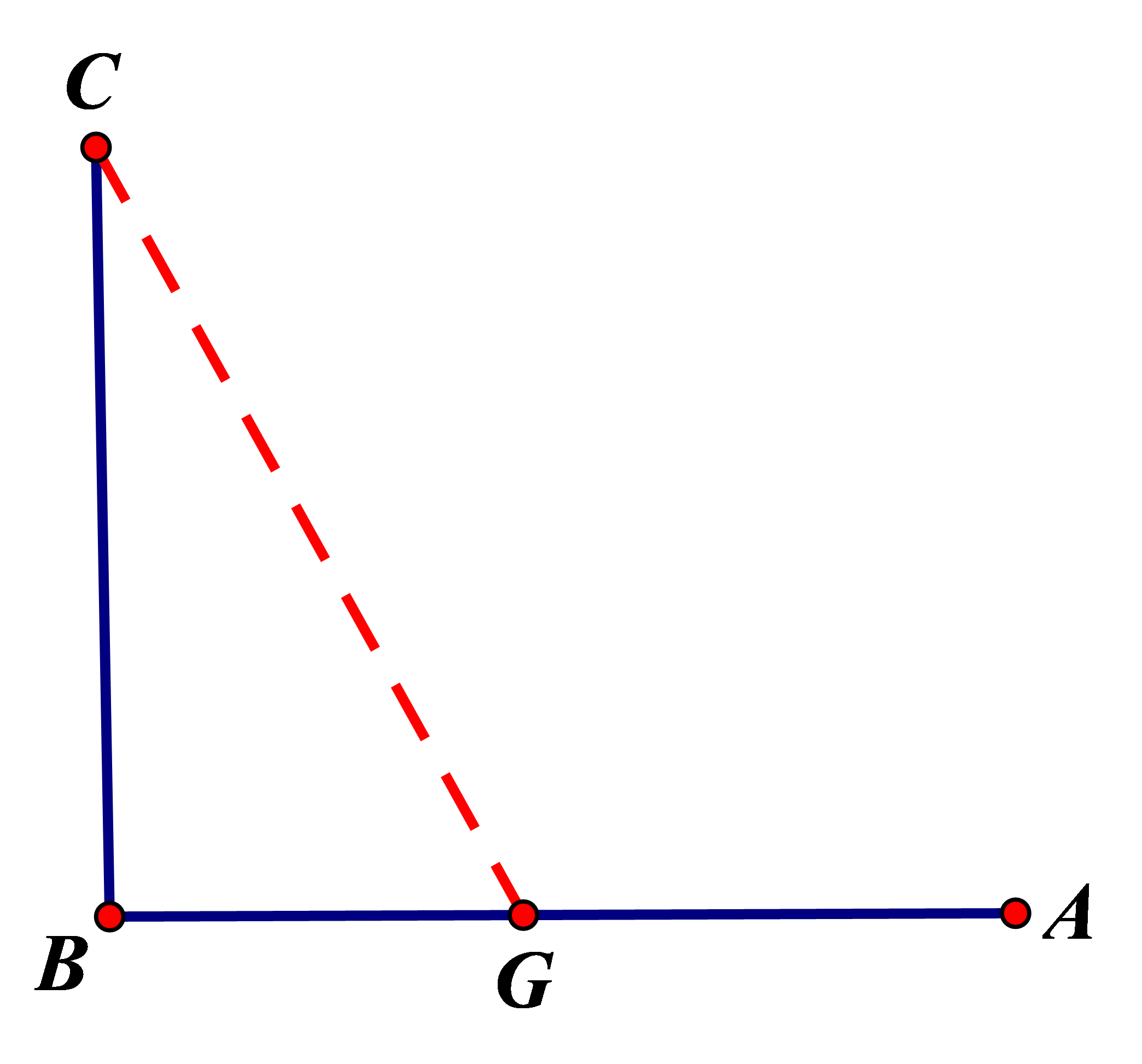
Gọi \(BG = x(0 < x < 100) \Rightarrow
AG = 100 - x\)
Ta có \(GC = \sqrt{BC^{2} + GC^{2}} =
\sqrt{x^{2} + 3600}\)
Chi phí mắc dây điện: \(f(x) = 3000.(100 -
x) + 5000\sqrt{x^{2} + 3600}\)
Khảo sát hàm ta được: \(x =
45\).
Ví dụ 3. Một người cần đi từ khách sạn \(A\)bên bờ biển đến hòn đảo \(C\). Biết rằng khoảng cách từ đảo \(C\)đến bờ biển là \(10\ km\), khoảng cách từ khách sạn \(A\) đến điểm \(B\) trên bờ gần đảo \(C\)nhất là \(40\
km\). Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên).
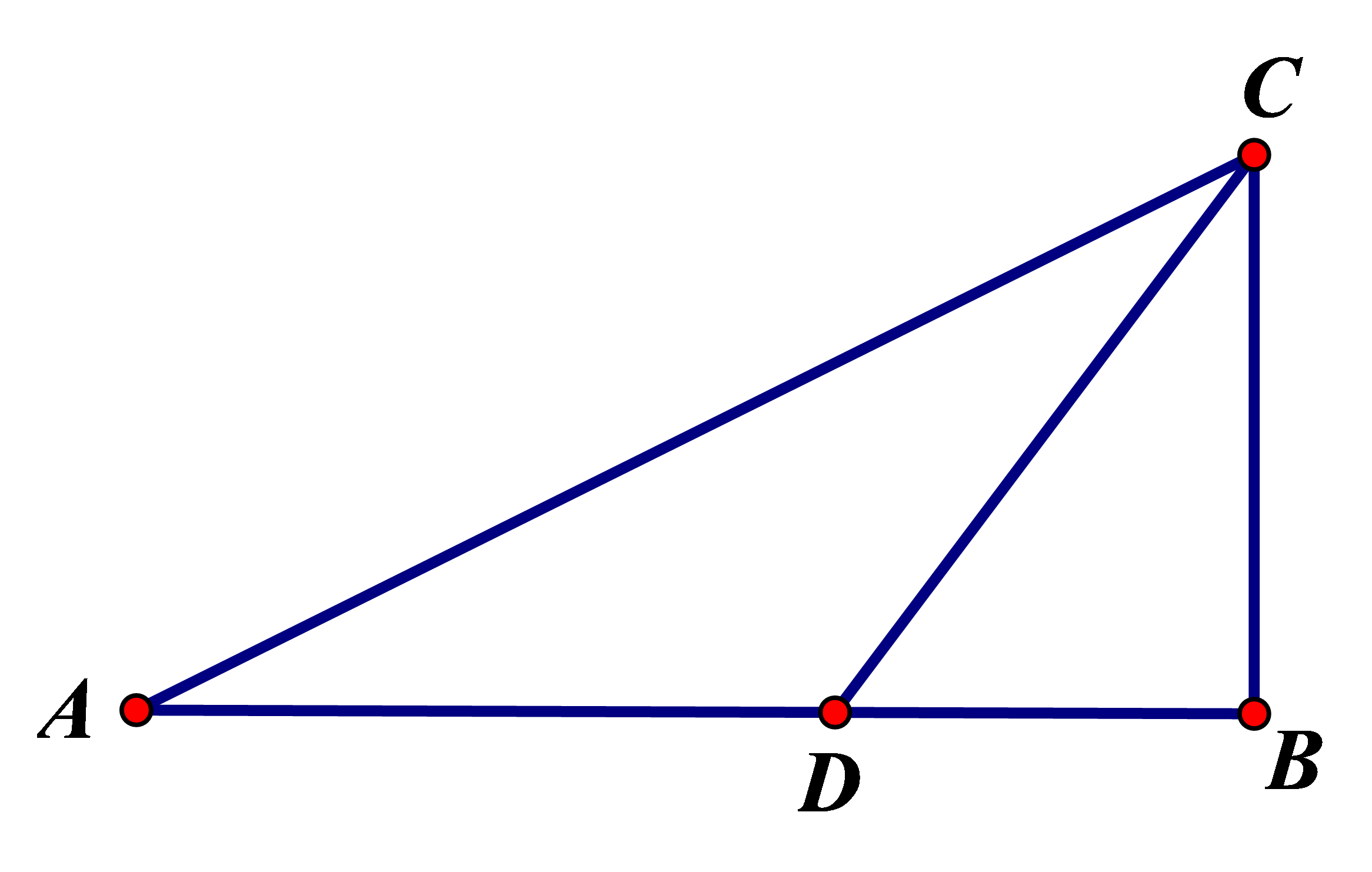
Biết kinh phí đi đường thủy là \(5USD/km\), đi đường bộ là \(3USD/km\). Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất? (\(AB = 40\ km\),\(BC = 10\ km\))
A. \(10\ km\). B. \(\frac{65}{2}\ km\). C. \(40\ km\). D. \(\frac{15}{2}\ km\).
Hướng dẫn giải
Chọn B
Đặt \(AD = x\ km\), \(x \in \lbrack 0;\ 40\rbrack \Rightarrow BD = 40 -
x\)
\(\Rightarrow CD = \sqrt{(40 - x)^{2} +
10^{2}}\).
Tổng kinh phí đi từ \(A\) đến \(C\) là \(f(x) =
x.3 + \sqrt{(40 - x)^{2} + 10^{2}}.5\).
\(f(x) = 3x + 5\sqrt{x^{2} - 80x +
1700}\).
\(f^{'(x)} = 3 + 5\frac{2x -
80}{2\sqrt{x^{2} - 80x + 1700}}\) \(\Leftrightarrow f'(x) =
\frac{3\sqrt{x^{2} - 80x + 1700} + 5x - 200}{\sqrt{x^{2} - 80x +
1700}}\).
\(f^{'(x)} = 0\)\(\Leftrightarrow 3\sqrt{x^{2} - 80x +
1700} = 200 - 5x \Leftrightarrow x = \frac{65}{2}\).
Bảng biến thiên:
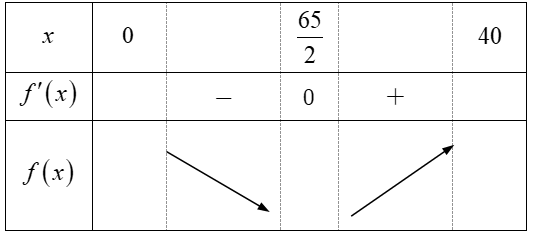
C. Bài tập vận dụng có hướng dẫn giải chi tiết
Bài tập 1. Một công ty dự kiến chi 1 tỷ đồng để sản xuất các thùng sơn hình trụ có dung tích \(5\)lít. Biết rằng chi phí để làm mặt xung quanh thùng đó là \(100.000\)đ/m2, chi phí để làm mỗi mặt đáy của thùng đó là \(120.000\)đ/m2. Hãy tính số thùng sơn tối đa mà công ty đó sản xuất được (Giả sử chi phí các mối nối không đáng kể).
A. \(18.209\) thùng. B. \(57.582\) thùng. C. \(12.525\) thùng. D. \(58.135\) thùng.
Bài tập 2. Nhà xe khoán cho hai tài xế ta-xi An và Bình mỗi người lần lượt nhận \(32\) lít và \(72\) lít xăng. Hỏi tổng số ngày ít nhất là bao nhiêu để hai tài xế chạy tiêu thụ hết số xăng của mình được khoán, biết rằng chỉ tiêu cho hai người một ngày tổng cộng chỉ chạy đủ hết \(10\)lít xăng?
A. 20 ngày. B. 15 ngày. C. 10 ngày. D. 25 ngày.
Bài tập 3. Ông An có một khu đất hình elip với độ dài trục lớn \(10\) m và độ dài trục bé \(8\)m. Ông An muốn chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là \(1000000\) đồng trên \(1m^{2}\) và chi phí trồng hoa là \(1200000\) đồng trên \(1m^{2}\). Hỏi ông An có thể thiết kế xây dựng như trên với tổng chi phí thấp nhất gần nhất với số nào sau đây?
A. \(67398224\) đồng. B. \(67593346\) đồng. C. \(63389223\) đồng. D. \(67398228\) đồng.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
-----------------------------------------------------------------
Việc luyện tập thường xuyên các bài toán thực tế về tối ưu chi phí không chỉ giúp học sinh củng cố kiến thức đạo hàm mà còn rèn luyện tư duy phân tích, mô hình hóa và giải quyết vấn đề hiệu quả. Với hệ thống bài tập từ dễ đến khó kèm lời giải chi tiết, người học có thể tự đánh giá năng lực và hoàn thiện kỹ năng làm bài một cách toàn diện.
Hy vọng tài liệu này sẽ trở thành nguồn tham khảo hữu ích trong quá trình ôn tập, góp phần giúp bạn tự tin đạt kết quả cao trong các bài kiểm tra và kỳ thi quan trọng của Toán 12.
