Cho hai biến cố và
, với
;
;
.
Tính .
Ta có
Trong quá trình ôn thi THPT Quốc gia môn Toán, việc nắm chắc các dạng bài xác suất có điều kiện ở mức độ thông hiểu và vận dụng là rất quan trọng để đạt điểm cao. Bài viết này tổng hợp hệ thống bài tập xác suất có điều kiện ở mức độ trung bình và nâng cao, đi kèm đáp án chi tiết và lời giải rõ ràng. Qua đó giúp bạn củng cố kiến thức, rèn luyện kỹ năng giải bài tập, đồng thời làm quen với các dạng đề thi thường gặp, tăng tự tin chinh phục kỳ thi quan trọng này.
Cho hai biến cố và
, với
;
;
.
Tính .
Ta có
Một nhóm học sinh có 30 học sinh, trong đó có 16 em học khá môn Toán, 25 em học khá môn Hóa học, 12 em học khá cả hai môn Toán và Hóa học. Chọn ngẫu nhiên một học sinh trong số đó. Tính xác suất để học sinh đó học khá môn Toán biết rằng học sinh đó học khá môn Hóa học.
Gọi A: “Học sinh đó học khá môn Toán”,
Và B: “Học sinh đó học khá môn Hóa học”.
Từ bài ra ta có ,
;
.
.
Một hộp chứa 8 bi xanh, 2 bi đỏ. Lần lượt bốc từng bi. Giả sử lần đầu tiên bốc được bi xanh. Xác định xác suất lần thứ 2 bốc được bi đỏ.
Gọi là biến cố lần
bốc được bi xanh.
Gọi là biến cố lần
bốc được bi đỏ.
Xác suất lần bốc được bi đỏ khi lần
đã bốc được bi trắng là
Ta có
Suy ra
Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6. Biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm.
Gọi là biến cố “con xúc xắc thứ nhất xuất hiện mặt 4 chấm”
Gọi là biến cố “Tổng số chấm xuất hiện trên 2 con xúc xắc bằng 6”.
Khi con xúc xắc thứ nhất đã xuất hiện mặt 4 chấm thì thì lần thứ hai xuất hiện 2 chấm thì tổng hai lần xuất hiện là 6 chấm thì
Một bình đựng 3 bi xanh và 2 bi trắng. Lấy ngẫu nhiên lần 1 một viên bi (không bỏ vào lại), rồi lần 2 một viên bi. Tính xác suất để lần 1 lấy một viên bi xanh, lần 2 lấy một viên bi trắng.
Gọi là biến cố “lấy một bi xanh lần thứ nhất” thì
.
Gọi là biến cố “lấy một bi trắng lần thứ hai”.
Gọi là biến cố “lấy lần 1 lấy một viên bi xanh, lần 2 lấy một viên bi trắng”.
Nếu đã xảy ra thì trong bình chỉ còn 2 bi xanh, 2 bi trắng.
Khi đó .
Mà , do đó theo công thức nhân ta có:
.
Trong một đội tuyển có ba vận động viên và
thi đấu với xác suất chiến thắng lần lượt là
và
. Giả sử mỗi người thi đấu một trận độc lập với nhau. Tính xác suất để
thua trong trường hợp đội tuyển thắng hai trận.
Gọi là biến cố “vận động viên
chiến thắng”, ta có
;
là biến cố “vận động viên
chiến thắng” thì
;
là biến cố “vận động viên
chiến thắng” thì
.
Gọi là biến cố “đội tuyển thắng hai trận”. Ta có
.
Vậy xác suất cần tính là
.
Trong một hộp kín có 10 viên bi vàng và 6 viên bi đỏ, các viên bi có cùng kích thước và khối lượng. Bạn Phong lấy ngẫu nhiên một viên bi từ trong hộp, không trả lại. Sau đó bạn Trung lấy ngẫu nhiên một trong 15 viên bi còn lại. Tính xác suất để Phong lấy được viên bi đỏ và Trung lấy được viên bi vàng.
Gọi là biến cố: "Bạn Phong lấy được viên bi đỏ ";
là biến cố: "Bạn Trung lấy được viên bi vàng ".
Vì nên
.
Nếu xảy ra tức là bạn Phong lấy được viên bi đỏ thì trong hộp có
viên bi với 10 viên bi vàng.
Vậy .
Theo công thức nhân xác suất: .
Vậy xác suất để Phong lấy được viên bi đỏ và Trung lấy được viên bi vàng bằng
Bốn quả bóng giống nhau được đánh số 1, 2, 3 và 4 rồi cho vào hộp. Một quả bóng được rút ngẫu nhiên ra khỏi hộp và không được trả lại vào hộp. Quả bóng thứ hai sau đó được rút ngẫu nhiên từ chiếc hộp. Xác suất để số đầu tiên được rút ra là số 2 nếu biết số đó tổng số ghi trê 2 quả lấy ra ít nhất là 4 bằng
Gọi A là biến cố quả thứ 2 rút ra mang số 2.
Gọi B là biến cố để tổng các số trên 2 quả lấy ra ít nhất là 4.
Ta có: .
Lại có: các cặp số có tổng ít nhất bằng 4 là:
Các cặp số có tổng ít nhất bằng 4 nhưng quả thứ 2 mang số 2 là
Do đó: ;
.
Vậy .
Chọn ngẫu nhiên một gia đình có người con. Tính xác suất để gia đình này có hai trai, một gái biết rằng gia đình có con gái.
Không gian mẫu là trong đó
ký hiệu con trai và
ký hiệu con gái.
Gọi là biến cố “Có hai trai, một gái”.
Ta có .
Gọi là biến cố “Gia đình có con gái”.
Ta có .
Có nên
.
Vậy .
Lớp 12A có học sinh, trong đó có
bạn nữ còn lại là nam. Có
bạn tên Hiền, trong đó có
bạn nữ và
bạn nam. Thầy giáo gọi ngẫu nhiên
bạn lên bảng. Xác suất để có tên Hiền, nhưng với điều kiện bạn đó nữ là
Gọi là biến cố “bạn học sinh được thầy giáo gọi lên bảng tên là Hiền”.
Gọi là biến cố “bạn học sinh được thầy giáo gọi lên bảng là nữ”.
Ta có ,
Xác suất để thầy giáo gọi bạn đó lên bảng có tên Hiền, nhưng với điều kiện bạn đó nữ là:
Một gia đình có 2 đứa trẻ. Biết rằng có ít nhất 1 đứa trẻ là con gái. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu? Cho biết xác suất để một đứa trẻ là trai hoặc gái là bằng nhau.
Giới tính cả 2 đứa trẻ là ngẫu nhiên và không liên quan đến nhau.
Do gia đình có 2 đứa trẻ nên sẽ có thể xảy ra 4 khả năng:
(trai, trai), (gái, gái), (gái, trai), (trai, gái).
Gọi A là biến cố “Cả hai đứa trẻ đều là con gái”
Gọi B là biến cố “Có ít nhất một đứa trẻ là con gái”
Ta có
Do nếu xảy ra A thì đương nhiên sẽ xảy ra B nên ta có:
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là
Lớp 12A có 45 học sinh gồm nam và
nữ. Trong kì kiểm tra cuối kì 2 môn Toán có
học sinh đạt điểm giỏi trong đó có
nam và
nữ. Gọi tên ngẫu nhiên một học sinh trong danh sách lớp. Tìm xác suất để gọi được học sinh đạt điểm giỏi môn Toán biết rằng học sinh đó là nữ .
Gọi A là biến cố “ Gọi được học sinh đạt điểm giỏi môn Toán”.
Gọi B là biến cố “ Gọi được học sinh nữ”.
Khi đó xác suất để gọi được học sinh đạt điểm giỏi môn Toán và là học sinh nữ là xác suất của biến cố A với điều kiện B.
Ta đi tính .
Ta có : ;
;
.
Suy ra : .
Giả sử trong một nhóm người có người là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là
, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là
. Tính xác suất để người được chọn ra không nhiễm bệnh và không có phản ứng dương tính.
Cách 1: Sơ đồ hình cây
Gọi : “Người được chọn ra không nhiễm bệnh”.
Và : “Người được chọn ra có phản ứng dương tính”
Theo bài ta có:
Do đó:
Ta có sơ đồ hình cây như sau:
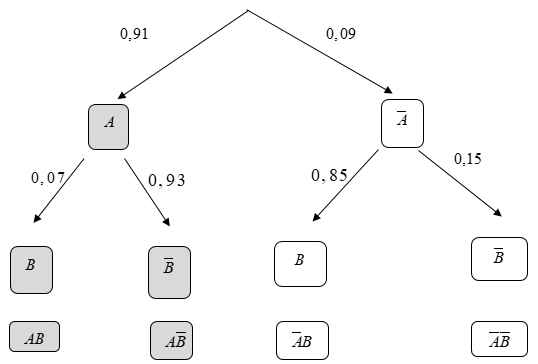
Vậy: .
Cách 2: Sử dụng công thức
Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn , biết rằng có ít nhất một con đã ra mặt 5 chấm.
Gọi : "ít nhất một con đã ra mặt 5 chấm".
Và : "tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10 ".
Ta có: .
Biến cố có các trường hợp
.
Biến cố có 3 trường hợp xảy ra:
có xác suất là:
.
Vậy .
Một nhóm 50 học sinh có 23 bạn biết chơi cầu lông mà không biết chơi bóng đá và 21 bạn biết chơi bóng đá mà không biết chơi cầu lông. Biết rằng mỗi học sinh trong nhóm này biết chơi bóng đá hoặc cầu lông. Chọn ngẫu nhiên một học sinh trong nhóm. Tính xác suất học sinh này biết chơi bóng đá, biết rằng bạn ấy biết chơi cầu lông.
Gọi là biến cố “học sinh được chọn biết chơi bóng đá”,
là biến cố “học sinh được chọn biết chơi cầu lông”.
Ta có và
.
Do đó .
Để được chọn vào đội tuyển học sinh giỏi môn Toán cấp thành phố, mỗi thí sinh phải vượt qua hai vòng thi. Bạn Hà tham dự cuộc tuyển chọn này. Xác suất để Hà qua được vòng thứ nhất là . Nếu qua được vòng thứ nhất thì xác suất để Hà qua được vòng thứ hai là
. Xác suất để bạn Hà được chọn vào đội tuyển này là
Gọi là biến cố: “Hà qua được vòng thứ nhất” và
là biến cố: “Hà qua được vòng thứ hai”. Khi đó biến cố: “Hà được chọn vào đội tuyển” là
.
Ta có .
Gieo hai con xúc sắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng . Biết rằng con xúc xắc thứ nhất xuất hiện mặt
chấm.
Gọi là biến cố “con xúc xắc thứ nhất xuất hiện mặt
chấm”
Gọi là biến cố “Tổng số chấm xuất hiện trên
con xác xắc bằng
”.
Khi con xúc xắc thứ nhất đã xuất hiện mặt chấm thì lần thứ hai xuất hiện
chấm thì tổng hai lần xuất hiện là
chấm thì
Một hộp chứa 8 bi trắng, 2 bi đỏ. Lần lượt bốc từng bi và không trả lại bi được bốc vào hộp. Giả sử lần đầu tiên bốc được bi trắng. Xác suất lần thứ 2 bốc được bi đỏ là
Gọi A là biến cố “lần 1 bốc được bi trắng”
Gọi B là biến cố “lần 2 bốc được bi đỏ”
Xác suất lần 2 bốc được bi đỏ khi lần 1 đã bốc được bi trắng là
Ta có: ;
Do đó: .
Một trường trung học phổ thông có 600 học sinh, trong đó có 245 học sinh nam và 355 học sinh nữ. Tổng kết học kỳ I, có 170 học sinh đạt danh hiệu học sinh giỏi, trong đó có 80 học sinh nam và 90 học sinh nữ. Chọn ra ngẫu nhiên một học sinh trong số 600 học sinh đó. Tính xác suất để học sinh được chọn có danh hiệu học sinh giỏi và là nam (làm tròn kết quả đến hàng phần trăm).
Xét hai biến cố sau:
A: "Học sinh được chọn ra đạt điểm giỏi";
: "Học sinh được chọn ra là học sinh nam".
Khi đó, xác suất để học sinh được chọn ra đạt danh hiệu học sinh giỏi và là nam, chính là xác suất của với điểu kiện
.
Do có 245 học sinh nam nên .
Vì thế, ta có;
Vậy xác suất để học sinh được chọn ra đạt danh hiệu học sinh giỏi và là nam bằng .
Một bình đựng 5 viên bi kích thước và chất liệu giống nhau, chỉ khác nhau về màu sắc. Trong đó có 3 viên bi xanh và 2 viên bi đỏ. Lấy ngẫu nhiên từ bình ra một viên bi ta được viên bi màu xanh, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được viên bi đỏ ở lần thứ hai.
Gọi : “lấy viên bi thứ nhất là màu xanh”.
Và : “lấy viên bi thứ hai là màu đỏ”.
Ta có: ;
.
Do đó: .
Để kiểm tra tính chính xác của một xét nghiệm nhằm chẩn đoán bệnh , người ta chọn một mẫu gồm
người, trong đó có
người mắc bệnh
và
người không mắc bệnh
để làm xét nghiệm. Trong số
người mắc bệnh
có
người cho kết quả dương tính. Trong số
người không mắc bệnh có
người cho kết quả dương tính. Chọn ngẫu nhiên một người trong mẫu. Tính xác suất để người đó mắc bệnh
nếu biết rằng người đó có xét nghiệm âm tính.
Ta có bảng sau đây

Gọi là biến cố “Người đó mắc bệnh
”,
là biến cố “Người đó có xét nghiệm âm tính”.
Khi đó là biến cố “Người đó vừa mắc bệnh
, vừa có xét nghiệm âm tính”.
Từ bảng trên, ta có ;
.
Vậy xác suất cần tính là .
Một nhóm học sinh có 20 học sinh, trong đó có 12 em thích học môn Toán, 10 em thích học môn Văn, 2 em không thích học cả hai môn Toán và Văn. Chọn ngẫu nhiên 1 học sinh, xác xuất để học sinh đó thích học môn Toán biết rằng học sinh đó thích học môn Văn là
Gọi là biến cố “học sinh đó thích học môn Toán”,
là biến cố “học sinh đó thích học môn Văn”
Xác suất để học sinh được chọn thích học môn Toán, biết học sinh đó thích học môn Văn chính là .
Ta có ,
,
Ta có
Gieo đồng thời hai con xúc sắc cân đối. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc sắc là , biết rằng có ít nhất một con xúc sắc xuất hiện mặt
chấm.
Gọi là biến cố “Tổng số chấm xuất hiện trên hai con xúc sắc là
” và
là biến cố “Có ít nhất một con xúc sắc xuất hiện mặt
chấm”.
Ta có
;
.
Suy ra .
Một hộp gồm một số viên bi cùng loại, chỉ khác màu, trong đó có 6 bi xanh, còn lại là bi màu đỏ. Minh lấy ngẫu nhiên 1 viên bi trong hộp (không bỏ lại), sau đó Minh lại lấy ngẫu nhiên tiếp 1 viên bi trong hộp. Biết xác suất để Minh lấy được cả hai viên bi màu xanh là…..Hỏi ban đầu trong túi có số viên bi đỏ là bao nhiêu?
Gọi là biến cố “Lần 1 Minh lấy được bi màu xanh”,
là biến cố “Lần 2 Minh lấy được bi có màu xanh”
Khi đó là biến cố “Cả hai lần Minh lấy được bi màu xanh”. Ta có
Gọi là số kẹo ban đầu trong túi
Ta có ,
.
Theo công thức nhân xác suất, ta có
Hay .
Vậy số bi đỏ trong túi ban đầu là bi
Cho một hộp kín có 6 thẻ ATM của ACB và 4 thẻ ATM của Vietcombank. Lấy ngẫu nhiên lần lượt 2 thẻ (lấy không hoàn lại). Tìm xác suất để lần thứ hai lấy được thẻ ATM của Vietcombank nếu biết lần thứ nhất đã lấy được thẻ ATM của ACB.
Gọi là biến cố “lần thứ hai lấy được thẻ ATM Vietcombank”,
là biến cố “lần thứ nhất lấy được thẻ ATM của ACB”.
Ta cần tìm .
Sau khi lấy lần thứ nhất (biến cố xảy ra) trong hộp còn lại
thẻ (trong đó có
thẻ Vietcombank) nên
.
Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là bao nhiêu?
Ta có:
: "học sinh đã làm đúng bài toán đầu tiên", thì
.
: "học sinh đã làm đúng bài toán thứ hai", thì
.
: "học sinh làm đúng cả hai bài toán", thì
.
Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là .
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của các dự án I và II lần lượt là và
. Khả năng thắng thầu của hai dự án là
. Gọi
lần lượt là biến cố thắng thầu dự án I và dự án II. Biết công ty thắng thầu dự án I, tìm xác suất công ty thắng thầu dự án II.
Gọi là biến cố “công ty thắng dự án II biết công ty thắng thầu dự án I”.
Ta có .
Cho hai biến cố và
có
và
. Tính
có kết quả là
Theo công thức nhân xác xuất, ta có:
Vì và
là hai biến cố xung khắc nên:
.
Khảo sát về sở thích uống trà sữa của 200 em học sinh theo giới tính và loại trà sữa ta được bảng số liệu sau:
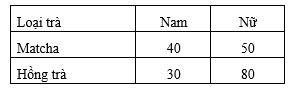
Chọn ngẫu nhiên một bạn học sinh. Nếu đã chọn được một bạn nữ thì xác suất để bạn nữ thích uống vị hồng trà là bao nhiêu?
Gọi A là biến cố “chọn được bạn nữ” suy ra .
B là biến cố “chọn được bạn thích uống hồng trà”.
Khi đó .
Nếu đã chọn được một bạn nữ thì xác suất để bạn nữ thích uống vị hồng trà là .
Cho hai biến cố và
có
. Tính
.
Theo công thức tính xác suất có điều kiện ta có:
.
Vì và
là hai biến cố xung khắc và
nên theo tính chất của xác suất, ta có:
.
Một hộp chứa 4 quả bóng được đánh số từ 1 đến 4. An lấy ngẫu nhiên một quả bóng, bỏ ra ngoài, rồi lấy tiếp một quả bóng nữa. Xét các biến cố:
: "Quả bóng lấy ra lần đầu có số chẵn"
: "Quả bóng lấy ra lần hai có số lẻ".
Tính xác suất có điều kiện .
Xác định không gian mẫu Ω và các biến cố.
Ta có .
⇒
;
⇒
.
Vậy .
Một lớp học có học sinh, mỗi học sinh giỏi ít nhất một trong hai môn Văn hoặc môn Toán. Biết rằng có
học sinh giỏi môn Toán và
học sinh giỏi môn Văn. Chọn ngẫu nhiên một học sinh. Tính xác suất để học sinh đó học giỏi môn Toán, biết rằng học sinh đó giỏi môn Văn.
Gọi là biến cố: “Học sinh được chọn giỏi môn Toán”,
là biến cố: “Học sinh được chọn giỏi môn Văn”.
Số học sinh giỏi cả hai môn là
Trong học sinh đó có đúng
học sinh giỏi môn Văn.
Vậy xác suất để học sinh được chọn giỏi môn Toán với điều kiện học sinh đó giỏi môn Văn là .
Cho hai biến cố và
, với
,
,
. Tính
.
Cách 1:
Ta có: .
Mà
Do đó
Cách 2:
Trong hộp có bút bi xanh và
bút bi đen, các chiếc bút có cùng kích thước và khối lượng. An lấy ngẫu nhiên
chiếc bút từ trong hộp, không trả lại. Sau đó bạn Bình lấy ngẫu nhiên một trong
chiếc bút còn lại. Tính xác suất để An lấy được bút xanh và Bình lấy được bút đen.
Xét hai biến cố sau:
A: “An lấy được bút xanh.”
B: “Bình lấy được bút đen.”
Ta cần tính . Vì
nên
.
Nếu A xảy ra tức là An lấy được bút xanh thì trong hộp còn bút bi với
bút đen. Vậy
.
Theo công thức nhân xác suất: .
Một lớp có 50 học sinh, trong đó có 30 học sinh nam và 20 học sinh nữ. Có 5 học sinh nam được học sinh giỏi và có 6 học sinh nữ được học sinh giỏi. Xác suất để chọn được một bạn nữ là học sinh giỏi
Gọi A là biến cố chọn được học sinh giỏi.
Gọi B là biến cố chọn được học sinh là nữ.
Khi đó
Xác suất để chọn được một học sinh nữ và học sinh đó là học sinh giỏi là:
Cho hai biến cố và
, với
,
,
. Tính
.
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
