Chuyên đề 12 Ứng dụng tọa độ không gian giải bài toán hình học
Giải toán hình học bằng tọa độ không gian
Bạn đang ôn luyện cho kỳ thi THPT quốc gia môn Toán và muốn nắm chắc kiến thức về hình học không gian? Trong Chuyên đề 12: Ứng dụng tọa độ không gian giải bài toán hình học, chúng ta sẽ cùng hệ thống lý thuyết, phương pháp giải nhanh và những dạng bài tập trọng tâm thường xuất hiện trong đề thi. Đây là nội dung quan trọng, giúp học sinh rèn kỹ năng tư duy logic và tăng tốc độ làm bài thi hiệu quả.
A. Đề bài trắc nghiệm Ứng dụng tọa độ không gian giải bài toán hình học
Câu 1: Cho tứ diện 
\(OABC\), có \(OA,OB,OC\)đôi một vuông góc và \(OA = 5,OB = 2,OC = 4\). Gọi \(M,N\) lần lượt là trung điểm của \(OB\)và \(OC\). Gọi \(G\) là trọng tâm của tam giác \(ABC\). Khoảng cách từ \(G\) đến mặt phẳng \((AMN)\) là:
A. \(\frac{20}{3\sqrt{129}}.\) B. \(\frac{20}{\sqrt{129}}.\) C. \(\frac{1}{4}.\) D. \(\frac{1}{2}.\)
Câu 2: Cho hình chóp \(S.ABCD\) đáy là hình thang vuông tại \(A\) và \(D\), \(SA\bot(ABCD)\). Góc giữa \(SB\) và mặt phẳng đáy bằng \(45^{o}\), \(E\) là trung điểm của \(SD\), \(AB =
2a\), \(AD = DC = a\). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \((ACE)\).
A. \(\frac{2a}{3}\). B. \(\frac{4a}{3}\). C. \(a\). D. \(\frac{3a}{4}\).
Câu 3: Trong không gian với hệ tọa độ \(Oxyz\), cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình chữ nhật. Biết \(A(0;0;0)\),\(D(2;0;0)\),\(B(0;4;0)\),\(S(0;0;4)\). Gọi \(M\) là trung điểm của \(SB\). Tính khoảng cách từ \(B\) đến mặt phẳng \((CDM)\).
A. \(d\left( B,(CDM) \right) =
2\). B. \(d\left( B,(CDM) \right) =
2\sqrt{2}\).
C. \(d\left( B,(CDM) \right) =
\frac{1}{\sqrt{2}}\). D. \(d\left( B,(CDM) \right) =
\sqrt{2}\).
Câu 4: Một phần sân trường được định vị bởi các điểm \(A,B,C,D\), như hình vẽ.
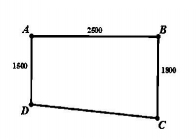
Bước đầu chúng được lấy “ thăng bằng” để có cùng độ cao, biết \(ABCD\) là hình thang vuông ở \(A\) và \(B\) với độ dài \(AB = 25\ m\), \(AD = 15\ m\), \(BC = 18\ m\). Do yêu cầu kĩ thuật, khi lát phẳng phần sân trường phải thoát nước về góc sân ở \(C\) nên người ta lấy độ cao ở các điểm \(B\), \(C\), \(D\) xuống thấp hơn so với độ cao ở \(A\) là \(10\ cm\), \(a\ cm\), \(6\
cm\)tương ứng. Giá trị của \(a\) là số nào sau đây?
A. \(15,7\ cm\). B. \(17,2\ cm\). C. \(18,1\ cm\). D. \(17,5\ cm\).
Câu 5: Một sân vận động được xây dựng theo mô hình là hình chóp cụt \(OAGD.BCFE\)có hai đáy song song với nhau. Mặt sân \(OAGD\) là hình chữ nhật và được gắn hệ trục \(Oxyz\) như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân \(OAGD\) có chiều dài \(OA = 100m\), chiều rộng \(OD = 60m\) và tọa độ điểm \(B(10;10;8)\).
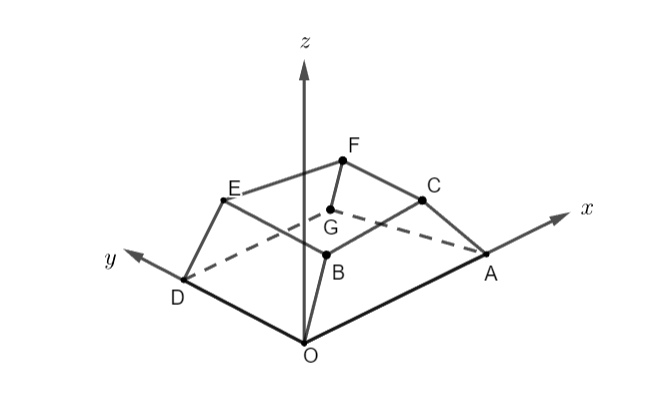
Tính khoảng cách từ điểm \(G\) đến mặt phẳng \((OBED)\).
A. \(62,5m\) B. \(64,7m\) C. \(60,2m\) D. \(63,2m\)
Câu 6: Một công trình đang xây dựng được gắn hệ trục \(Oxyz\) (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường \((P),(Q),(R)\) (như hình vẽ) của tòa nhà lần lượt có phương trình: \((P):x + 2y - 2z + 1 = 0\), \((Q):2x + y + 2z - 3 = 0\),\((R):2x + 4y - 4z - 19 = 0\).
Tính khoảng giữa hai bức tường \((P)\) và \((R)\) của tòa nhà.
A. \(4,2m\) B. \(3,5m\) C. \(4,5m\) D. \(4,0m\)
Câu 7: Một công trình đang xây dựng được gắn hệ trục \(Oxyz\) (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường \((P),(Q),(R),(T)\) (như hình vẽ) của tòa nhà lần lượt có phương trình: \((P):2x - y - z + 1 = 0\), \((Q):x + 3y - z - 2 = 0\),\((R):4x - 2y - 2z + 9 = 0\),\((T):2x + 6y - 2z + 15 = 0\).
Tính chiều rộng bức tường \((Q)\)của tòa nhà.
A. \(2,9m\) B. \(2,5m\) C. \(3,2m\) D. \(3,3m\)
Câu 8: Trong không gian với hệ trục tọa độ \(Oxyz\), cho bốn điểm \(S( - 1;6;2),A(0;0;6),B(0;3;0),C( -
2;0;0)\). Gọi \(H\) là chân đường cao vẽ từ \(S\) của tứ diện \(S.ABC\). Lập phương trình mặt phẳng đi qua ba điểm \(S;H;B\).
A. \(x + 5y - 7z - 15 = 0\) B. \(2x + 3y + z - 7 = 0\)
C. \(5x - y + 3z - 1 = 0\) D. \(x - 2y + 3z - 5 = 0\)
Câu 9: Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a\), \(\widehat{ABC} = 60^{0}\), mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(H,M,N\) lần lượt là trung điểm các cạnh \(AB,SA,SD\) và \(P\) là giao điểm của \((HMN)\) với \(CD\). Khoảng cách từ trung điểm \(K\) của đoạn thẳng \(SP\) đến mặt phẳng \((HMN)\) bằng:
A. \(\frac{a\sqrt{15}}{30}\) B. \(\frac{a\sqrt{15}}{20}\) C. \(\frac{a\sqrt{15}}{15}\) D. \(\frac{a\sqrt{15}}{10}\)
Câu 10: Cho hình vuông \(ABCD\) có cạnh \(a\). Trên hai tia \(Bt,Ds\) vuông góc và nằm cùng phía với mặt phẳng \((ABCD)\) lần lượt lấy hai điểm \(E;F\) sao cho \(BE = \frac{a}{2};DF = a\). Tính góc \(\varphi\) giữa hai mặt phẳng \((AEF);(CEF)\).
A. \(\varphi = 30^{0}\) B. \(\varphi = 90^{0}\) C. \(\varphi = 60^{0}\) D. \(\varphi = 45^{0}\)
B. Đáp án tổng quan bài tập trắc nghiệm
|
1 - A |
2 - B |
3 - D |
4 - B |
5 - A |
6 – B |
|
7 - A |
8 - A |
9 - B |
10 - B |
11 - D |
12 - A |
C. Hướng dẫn giải chi tiết bài tập trắc nghiệm
Câu 1:
Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ.
Ta có \(O(0;0;0)\), \(A \in Oz,\ \ B \in Ox,\ \ C \in Oy\)sao cho \(AO = 5,\ \ OB = 2,\ \ OC = 4\)
\(\Rightarrow A(0;0;5),\ \ B(2;0;0),\ \
C(0;4;0)\).
Khi đó: \(G\) là trọng tâm tam giác\(ABC\) nên \(G\left( \frac{2}{3};\frac{4}{3};\frac{5}{3}
\right)\)
\(M\)là trung điểm \(OB\)nên \(M(1;0;0)\)
\(N\)là trung điểm \(OC\)nên \(N(0;2;0)\).
Phương trình mặt phẳng \((AMN)\)là: \(\frac{x}{1} + \frac{y}{2} + \frac{z}{5} =
1\) hay \(10x + 5y + 2z - 10 =
0\)
Vậy khoảng cách từ \(G\) đến mặt phẳng \((AMN)\)là:
\(d\left( G,(AMN) \right) = \frac{\left|
\frac{20}{3} + \frac{20}{3} + \frac{10}{3} - 10 \right|}{\sqrt{100 + 25
+ 4}} = \frac{20}{3\sqrt{129}}\).
Câu 2:
Hình vẽ minh họa
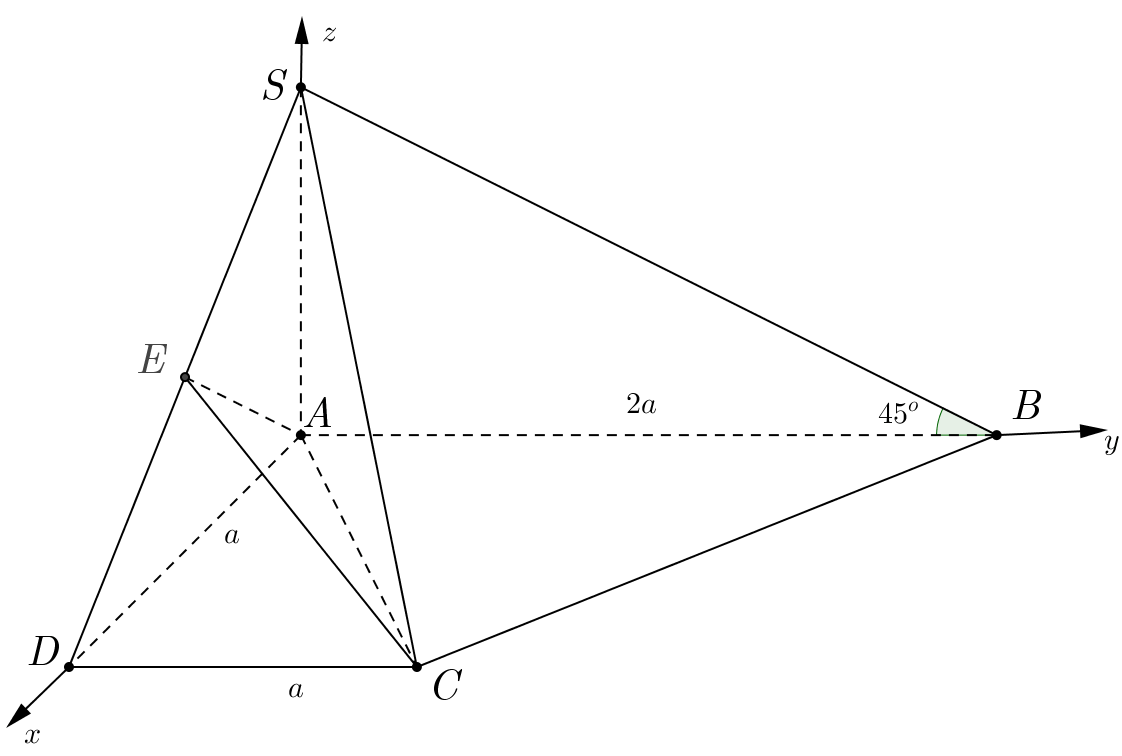
Hình chiếu của \(SB\) trên mặt phẳng \((ABCD)\) là \(AB\) \(\Rightarrow\) Góc giữa \(SB\) và mặt đáy là góc giữa \(SB\) và \(AB\) và bằng góc \(\widehat{SBA} = 45^{o}\).
Tam giác \(SAB\) vuông cân tại \(A\) \(\Rightarrow
SA = 2a\).
Chọn hệ trục tọa độ như hình vẽ ta có: \(A(0;0;0)\), \(B(0;2a;0)\), \(C(a;a;0)\), \(D(a;0;0)\), \(S(0;0;2a)\), \(E\left( \frac{a}{2};0;a \right)\).
\(\overrightarrow{AC} = (a;a;0)\), \(\overrightarrow{AE} = \left( \frac{a}{2};0;a
\right) \Rightarrow \overrightarrow{AC} \land \overrightarrow{AE} =
\left( a^{2}; - a^{2}; - \frac{a^{2}}{2} \right)\)
\(\Rightarrow\) mặt phẳng \((ACE)\) có véctơ pháp tuyến \(\overrightarrow{n} = (2; - 2; - 1) \Rightarrow
(ACE):2x - 2y - z = 0\).
Vậy \(d\left( B,(ACE) \right) =
\frac{|2.2a|}{\sqrt{4 + 4 + 1}} = \frac{4a}{3}\).
Câu 3:
Hình vẽ minh họa:
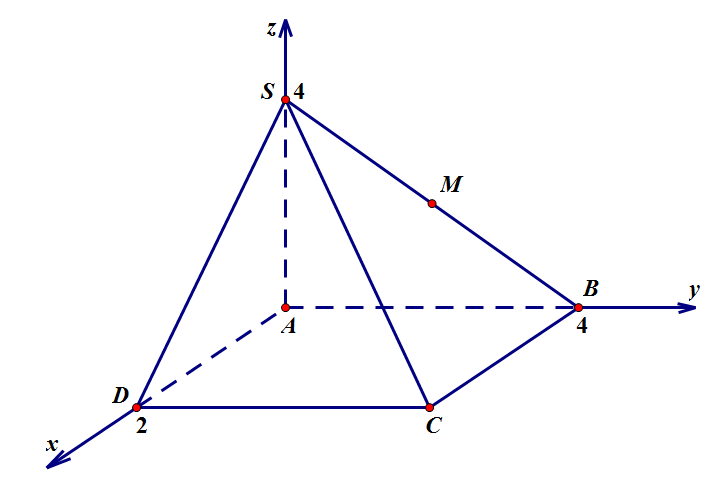
Tứ giác \(ABCD\) là hình chữ nhật nên \(\left\{ \begin{matrix}
x_{A} + x_{C} = x_{B} + x_{D} \\
y_{A} + y_{C} = y_{B} + y_{D} \\
z_{A} + z_{C} = z_{B} + z_{D}
\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}
x_{C} = 2 \\
y_{C} = 4 \\
z_{C} = 0
\end{matrix} \right.\ \Rightarrow C(2;4;0)\).
\(M\) là trung điểm của \(SB\) \(\Rightarrow M(0;2;2)\).
Viết phương trình mặt phẳng \((CDM)\):
\(\overrightarrow{CD} = (0; -
4;0)\), \(\overrightarrow{CM} = ( - 2;
- 2;2) \Rightarrow \overrightarrow{CD} \land \overrightarrow{CM} = ( -
8;0; - 8)\).
\((CDM)\) có một véc tơ pháp tuyến \(\overrightarrow{n} = (1;0;1)\).
Suy ra \((CDM)\) có phương trình: \(x + z - 2 = 0\).
Vậy \(d\left( B;(CDM) \right) = \frac{|0 +
0 - 2|}{\sqrt{1^{2} + 0^{2} + 1^{2}}} = \sqrt{2}\).
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
---------------------------------------------------------------------
Trên đây là toàn bộ kiến thức cốt lõi của Chuyên đề 12: Ứng dụng tọa độ không gian giải bài toán hình học trong chương trình ôn thi THPT quốc gia môn Toán. Hy vọng bài viết đã giúp bạn hiểu rõ cách vận dụng tọa độ không gian để xử lý các dạng toán hình học khó. Hãy luyện tập thêm các đề minh họa và đề thi chính thức để nâng cao kỹ năng, từ đó tự tin đạt điểm cao trong kỳ thi sắp tới.
