Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập Phương trình mặt cầu mức độ Vận dụng cao Toán 12 có đáp án

Ôn thi THPT Quốc gia môn Toán

Phương trình mặt cầu toán 12 có đáp án

Bạn đang ôn luyện cho kỳ thi THPT Quốc gia và muốn chinh phục điểm 9, 10 môn Toán? Bài viết này sẽ giúp bạn rèn luyện kỹ năng giải bài tập phương trình mặt cầu Toán 12 ở mức độ vận dụng cao, kèm theo đáp án chi tiết và hướng dẫn giải. Các bài toán được chọn lọc sát đề thi thật, giúp học sinh nâng cao tư duy hình học không gian, nắm chắc kiến thức và tự tin bước vào kỳ thi.

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 25 câu
  • Điểm số bài kiểm tra: 25 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng cao
    Tính giá trị nhỏ nhất của OI

    Trong không gian với hệ tọa độ Oxyz, cho A(a;0;0),B(0;b;0),C(0;0;c) với a;b;c là các số thực thay đổi, khác 0 và thỏa mãn a + b + c = 0. Gọi tâm mặt cầu ngoại tiếp tứ diện OABC là I. Giá trị nhỏ nhất của OI bằng

    Hướng dẫn:

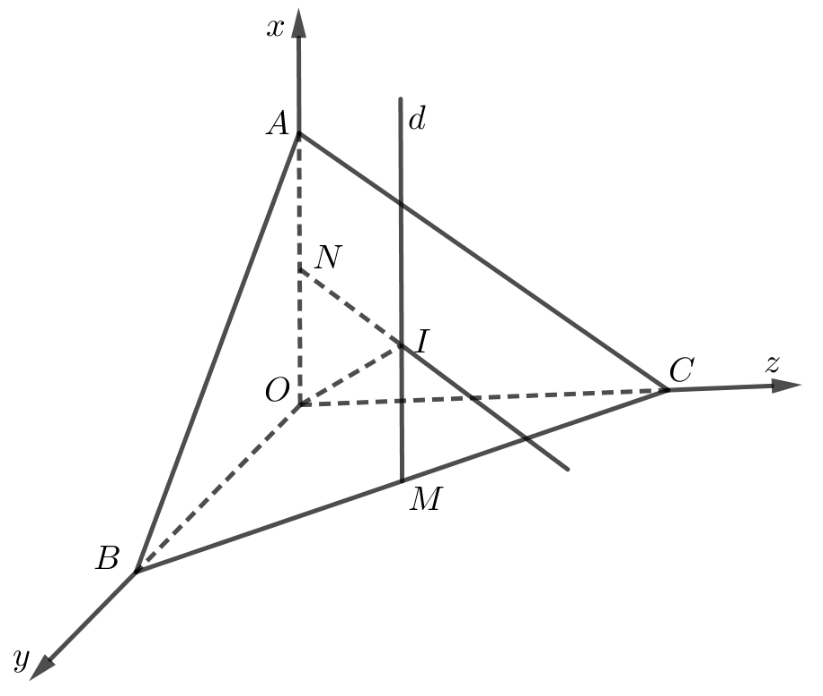
    Ta có OABC là tứ diện vuông tại O. Gọi M là trung điểm BC. Đường thẳng d qua M song song với OA là trục đường tròn ngoại tiếp tam giác OBC.

    Trong mặt phẳng (OA;d), từ trung điểm N của đoạn OA kẻ đường thẳng \Delta vuông góc với OA tại N cắt d tại I. Khi đó I là tâm mặt cầu ngoại tiếp tứ diện OABC.

    Ta có tọa độ điểm M\left( 0;\frac{b}{2};\frac{c}{2} \right), khi đó điểm I\left( \frac{a}{2};\frac{b}{2};\frac{c}{2} \right).

    Do đó OI = \sqrt{\left( \frac{a}{2} \right)^{2} + \left( \frac{b}{2} \right)^{2} + \left( \frac{c}{2} \right)^{2}} = \frac{1}{2}\sqrt{a^{2} + b^{2} + c^{2}} > \frac{a + b + c}{2\sqrt{3}} = \sqrt{3}.

    Dấu bằng xảy ra \Leftrightarrow a = b = c = 2

  • Câu 2: Vận dụng cao
    Tính thể tích khối tứ diện

    Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(a;0;0),B(0;b;0),C(0;0;c), trong đó a > 0,b > 0,c > 0 và \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7. Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (y - 3)^{2} = \frac{72}{7}. Thể tích của khối tứ diện OABC là.

    Hướng dẫn:

    Cách 1:

    Ta có : (ABC):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 \Leftrightarrow bcx + acy + abz - abc = 0.

    Theo bài ra có: \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7 \Leftrightarrow bc + 2ca + 3ab = 7abc.

    Mặt phẳng (ABC) tiếp xúc với mặt cầu (S) \Rightarrow d\left( I;(ABC) \right) = R

    \Leftrightarrow \frac{|bc + 2ca + 3ab - abc|}{\sqrt{b^{2}c^{2} + c^{2}a^{2} + a^{2}b^{2}}} = \sqrt{\frac{72}{7}}

    \Leftrightarrow \frac{1}{36}\left( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \right) = \frac{7}{72} \Leftrightarrow \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} = \frac{7}{2}.

    Ta có \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7

    \Leftrightarrow 7 = \left( \frac{1}{a} + 2.\frac{1}{b} + 3.\frac{1}{c} \right)^{2} \leq (1 + 4 + 9)\left( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \right).

    Dấu bằng xảy ra \Leftrightarrow \left\{\begin{matrix}a = 2b = 3c \\\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} a = 2 \\b = 1 \\c = \frac{2}{3}\end{matrix} \right..

    VậyV_{OABC} = \frac{1}{6}abc = \frac{1}{6}.2.1.\frac{2}{3} = \frac{2}{9}.

    Cách 2:

    Ta có (ABC):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 và \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7 suy ra M\left( \frac{1}{7};\frac{2}{7};\frac{3}{7}\right)\in (ABC).

    Lại có M\left( \frac{1}{7};\frac{2}{7};\frac{3}{7} \right) \in (S) nên (ABC) tiếp xúc với (S) tại M.

    Suy ra (ABC):\frac{x}{2} + \frac{y}{1} + \frac{z}{\frac{2}{3}} = 1 nên V_{OABC} = \frac{1}{6}abc = \frac{1}{6}.2.1.\frac{2}{3} = \frac{2}{9}.

  • Câu 3: Vận dụng cao
    Viết phương trình đường thẳng

    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:\frac{x - 13}{- 1} = \frac{y + 1}{1} = \frac{z}{4} và mặt cầu (S):x^{2} + y^{2} + z^{2} - 2x - 4y - 6z - 67 = 0. Qua d dựng các mặt phẳng tiếp xúc với (S) lần lượt tại T_{1};T_{2}. Viết phương trình đường thẳng T_{1}T_{2}.

    Hướng dẫn:

    Ta có mặt cầu (S) có tâm I(1;2;3), bán kính R = 3.

    Đường thẳng d đi qua điểm A(13; - 1;0), có vectơ chỉ phương \overrightarrow{u}( - 1;1;4).

    Mặt phẳng (P) chứa d có dạng (P):A(x - 13) + B(y + 1) + Cz = 0 ,\left( A^{2} + B^{2} + C^{2} \neq 0 \right)

    Do d \subset (P) nên ta có - 1.A + 1.B + 4.C = 0 \Leftrightarrow B = A - 4C.

    Ta có điều kiện tiếp xúc: R = d\left( I;(P) \right) \Leftrightarrow 9 = \frac{| - 12A + 3B + 3C|}{\sqrt{A^{2} + B^{2} + C^{2}}}

    \Leftrightarrow 9 = \frac{|9A + 9C|}{\sqrt{2A^{2} + 17B^{2} - 8AC^{2}}} \Leftrightarrow \left\lbrack \begin{matrix} A = 2C \\ A = 8C \end{matrix} \right.

    Suy ra hai mặt phẳng tiếp diện là \left( P_{1} \right):2x - 2y + z - 28 = 0, \left( P_{2} \right):8x + 4y + z - 100 = 0.

    Suy ra tọa độ các tiếp điểm T_{1}(7; - 4;6),T_{2}(9;6;4) \Rightarrow T_{1}T_{2}:\frac{x - 7}{1} = \frac{y + 4}{5} = \frac{z - 6}{- 1}

  • Câu 4: Vận dụng cao
    Chọn đáp án đúng

    Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu

    (S):x^{2} + y^{2} + z^{2} + ax + by + cz + d = 0 có bán kính R = \sqrt{19} đường thẳng d:\left\{\begin{matrix}x = 5 + t \\y = - 2 - 4t \\z = - 1- 4t\end{matrix} \right. và mặt phẳng (P):3x - y - 3z - 1 = 0 Trong các số \left\{ a;b;c;d \right\} theo thứ tự dưới đây, số nào thỏa mãn a + b + c + d = 43 đồng thời tâm I của (S) thuộc đường thẳng d và (S) tiếp xúc mặt phẳng (P)?

    Hướng dẫn:

    Ta có I \in d \Rightarrow I(5 + t;2 - 4t; - 1 - 4t)

    Do (S) tiếp xúc với (P) nên d\left( I;(P) \right) = R = \sqrt{19}

    \Leftrightarrow |19 + 19t| = 19 \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = - 2 \end{matrix} \right.

    Mặt khác (S) có tâm I\left( \frac{- a}{2};\frac{- b}{2};\frac{- c}{2} \right); bán kính R = \sqrt{\frac{a^{2} + b^{2} + c^{2}}{4} - d} = \sqrt{19}

    Xét khi t = 0 \Rightarrow I(5; - 2; - 1) \Rightarrow \left\{ a;b;c;d \right\} = \left\{ - 10;4;2;47 \right\}

    Do \frac{{{a^2} + {b^2} + {c^2}}}{4} - d \ne 19 nên ta loại trường hợp này

    Xét khi t = 2 \Rightarrow \left\{ {a;b;c;d} \right\} = \left\{ { - 6; - 12; - 14;75} \right\}

    Do \frac{a^{2} + b^{2} + c^{2}}{4} - d \neq 19 nên thỏa mãn.

  • Câu 5: Vận dụng cao
    Chọn phương án thích hợp

    Trong không gian Oxyz, cho đường thẳng \Delta:\left\{ \begin{matrix} x = 3 + t \\ y = - 1 - t \\ x = - 2 + t \end{matrix} \right., điểm M(1;2; - 1)và mặt cầu (S): x^{2} + y^{2} + z^{2} - 4x + 10y + 14z + 64 = 0. Gọi (\Delta') là đường thẳng đi qua M và cắt \Delta tại A, cắt (S) tại B sao cho \frac{AM}{AB} = \frac{1}{3} và điểm B có hoành độ là số nguyên. Mặt phẳng trung trực của đoạn AB có phương trình là

    Hướng dẫn:

    Từ giả thiết: (S) có tâm I(2; - 5; - 7) và bán kính R = \sqrt{14}.

    A \in \Delta \Rightarrow A(3 + t; - 1 - t; - 2 + t) \Rightarrow \overrightarrow{AM} = ( - 2 - t;t + 3;1 - t).

    Vì \frac{AM}{AB} = \frac{1}{3} \Rightarrow \overrightarrow{AB} = \pm 3\overrightarrow{AM}.

    +) Nếu \overrightarrow{AB} = 3\overrightarrow{AM} = ( - 3t - 6;3t + 9;2 - 3t) \Rightarrow B( - 2t - 3;2t + 8; - 2t + 1).

    Do B \in (S) \Rightarrow BI = R

    \begin{matrix} \Rightarrow {\left( {2t + 5} \right)^2} + {\left( { - 2t - 13} \right)^2} + {\left( {2t - 8} \right)^2} = 14 \hfill \\ \Rightarrow 12{t^2} + 40t + 244 = 0\left( {VN} \right) \hfill \\ \end{matrix}

    +) Nếu \overrightarrow {AB} = 3\overrightarrow {AM} = \left( { - 3t - 6;3t + 9;2 - 3t} \right)\Rightarrow B\left( { - 2t - 3;2t + 8; - 2t + 1} \right).

    Do  B \in (S) \Rightarrow BI = R 

    \Rightarrow (2t + 5)^{2} + ( - 2t - 13)^{2} + (2t - 8)^{2} = 14

    \Leftrightarrow 48t^{2} + 112t + 64 = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = - \frac{4}{3} \\ t = - 1 \end{matrix} \right..

    Do B có hoành độ là số nguyên nên t = - 1 \rightarrow \overrightarrow{AB} = (3; - 6; - 6).

    Trung điểm AB là E\left( \frac{7}{2}; - 3; - 6 \right) nên phương trình mặt phẳng trung trực AB:

    3x - 6y - 6z - \frac{129}{2} = 0.

  • Câu 6: Vận dụng cao
    Tính giá trị của biểu thức T

    Trong không gian hệ trục tọa độ Oxyz, cho hai điểm A(3; - 2;6),B(0;1;0) và mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 25. Mặt phẳng (P):ax + by + cz - 2 = 0 đi qua A,B và cắt (S) theo giao tuyến là hình tròn có bán kinh nhỏ nhất. Tính T = a + b + c?

    Hướng dẫn:

    Hình vẽ minh họa

    Mặt cầu (S) có tâm I(1;2;3) bán kính R = 5.

    Mặt phẳng (P) có vtpt \overrightarrow{n_{p}} = (a;b;c);\left( a^{2} + b^{2} + c^{2} \neq 0 \right).

    Do B(0;1;0) \in (P):b - 2 = 0 \Leftrightarrow b = 2.

    Ta có: \overrightarrow{AB} = ( - 3;3; - 6) = - 3(1; - 1;2), phương trình đường thẳng AB:\left\{ \begin{matrix} x = t \\ y = 1 - t \\ z = 2t \end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)

    Gọi r là bán kính của đường tròn giao tuyến, K là hình chiếu của I trên AB, H là hình chiếu vuông góc của I lên mặt phẳng (P).

    Ta có: K \in AB \Rightarrow K(t;1 - t;2t)

    \Rightarrow \overrightarrow{IK} = (t - 1; - t - 1;2t - 3)

    IK\bot AB \Rightarrow \overrightarrow{AB}.\overrightarrow{IK} = 0 \Rightarrow t = 1 \Rightarrow \overrightarrow{IK} = (0; - 2; - 1)

    r = \sqrt{R^{2} - d^{2}\left( I;(P) \right)} = \sqrt{25 - d^{2}\left( I;(P) \right)} = \sqrt{25 - IH^{2}}

    Ta có: r đạt min thì IH đạt max.

    Mà IH \leq IK \Rightarrow IH_{\min} \Leftrightarrow H \equiv K \Rightarrow (P)\bot IK \Rightarrow\overrightarrow{n_{P}},\overrightarrow{IK} cùng phương

    \Rightarrow \overrightarrow{n_{P}} = k.\overrightarrow{IK} \Rightarrow \left\{ \begin{matrix} a = 0 \\ b = - 2k = 2 \\ c = - k \end{matrix} \right.

    \Rightarrow \left\{ \begin{matrix} a = 0 \\ k = - 1 \\ b = 2 \\ c = 1 \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} a = 0 \\ b = 2 \\ c = 1 \end{matrix} \right.

  • Câu 7: Vận dụng cao
    Tính giá trị nhỏ nhất của biểu thức S

    Trong không gian Oxyz cho mặt cầu (S) có phương trình x^{2} + y^{2} + z^{2} - 4x + 2y - 2z - 3 = 0 và điểm A(5;3; - 2). Một đường thẳng d thay đổi luôn đi qua A và luôn cắt mặt cầu tại hai điểm phân biệt M,N. Tính giá trị nhỏ nhất của biểu thức S = AM + 4AN.

    Hướng dẫn:

    Tâm I(2; - 1;1) và bán kính mặt cầu R = 3

    AI = \sqrt{(2 - 5)^{2} + ( - 1 - 3)^{2} + (1 + 2)^{2}} = \sqrt{34}

    Gía trị nhỏ nhất xảy ra trong trường hợp AM > AN

    Đặt AN = x \Rightarrow \sqrt{34} - 3 \leq x < 5

    AM.AN = 25 \Rightarrow AM = \frac{25}{x}

    S = 4AM + AN = 4x + \frac{25}{x} = f(x)

    Xét f(x) = 4x + \frac{25}{x} trên \left\lbrack \sqrt{34} - 3;5 \right)

    f'(x) = 4 + \frac{25}{x^{2}} = \frac{4x^{2} - 25}{x^{2}} > 0;\forall x \in \left\lbrack \sqrt{34} - 3;5 \right)

    \Rightarrow S_{\min} khi x = \sqrt{34} - 3

    S_{\min} = 4\left( \sqrt{34} - 3 \right) + \frac{25}{\sqrt{34} - 3} = 5\sqrt{34} - 9

    Vậy GTNN S_{\min} = 5\sqrt{34} - 9 khi x = \sqrt{34} - 3.

  • Câu 8: Vận dụng cao
    Tính giá trị nhỏ nhất của bán kính mặt cầu

    Trong không gian với hệ trục tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A\left( {1;6;2} \right),B\left( {3;0;0} \right) và có tâm thuộc mặt phẳng (P):x - y + 2 = 0 bán kính của mặt cầu (S) có giá trị nhỏ nhất là

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi H là trung điểm của đoạn thẳng AB nên H(2; 3; 1). Vecto \overrightarrow{HB} = (1; - 3; - 1).

    Mặt cầu đi qua A, B có tâm M thuộc mặt phẳng (Q)

    là mặt phẳng trung trực của đoạn thẳng AB

    qua H và có vecto pháp tuyến \overrightarrow{HB} = (1; - 3; - 1) có phương trình (Q):x - 3y + z + 6 = 0.

    Do tâm M của mặt cầu cũng thuộc (P) nên M thuộc đường thẳng (d) là giao của (P) và (Q) có vectơ chỉ phương \overrightarrow{u} = (1;1;2) và qua M_{0}( - 2;0;4).

    Gọi d là khoảng cách từ H đến (d), d = d\left( H;(d) \right) = \frac{\left| \left\lbrack \overrightarrow{M_{0}H};\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{\sqrt{66}}{6},HB = \sqrt{11}.

    Ta có R = MB = \sqrt {H{B^2} + M{H^2}}. Nhận thấy HB không đổi, R nhỏ nhất khi MH nhỏ nhất, MH nhỏ nhất khi M trùng I, lúc đó MH = HI = d = \frac{{\sqrt {66} }}{6}. (I là hình chiếu vuông góc của H lên (d))

    Vậy R = MB = \sqrt{HB^{2} + IH^{2}} = \sqrt{\frac{66}{36} + 11} = \frac{\sqrt{462}}{6}.

  • Câu 9: Vận dụng cao
    Tìm giá trị của m thỏa mãn điều kiện

    Trong không gian tọa độ Oxyzcho mặt cầu (S):x^{2} + y^{2} + z^{2} + 4x - 6y + m = 0 và đường thẳng \Delta là giao tuyến của hai mặt phẳng (\alpha):x + 2y - 2z - 4 = 0 và (\beta):2x - 2y - z + 1 = 0. Đường thẳng \Delta cắt mặt cầu (S) tại hai điểm phân biệt A,B thỏa mãn AB = 8 khi:

    Hướng dẫn:

    Ta có \left\{ \begin{matrix} x + 2y - 2z - 4 = 0 \\ 2x - 2y - z + 1 = 0 \end{matrix} \right..

    Phương trình tham số của \Delta là \left\{ \begin{matrix} x = - 2 + 2t \\ y = t \\ z = - 3 + 2t \end{matrix} \right..

    A \in (\Delta) \Rightarrow A( - 2 + 2t;t; - 3 + 2t).

    A \in (S) \Rightarrow ( - 2 + 2t)^{2} + t^{2} + ( - 3 + 2t)^{2} + 4( - 2 + 2t) - 6t + m = 0 (*).

    (*) \Leftrightarrow 9t^{2} - 18t + 5 + m = 0.

    Phương trình (*) có hai nghiệm phân biệt khi \Delta' = 36 - 9m > 0 \Leftrightarrow m < 4.

    Khi đó A\left( - 2 + 2t_{1};t_{1}; - 3 + 2t_{1} \right),B\left( - 2 + 2t_{2};t_{2}; - 3 + 2t_{2} \right).

    t_{1} + t_{1} = 2,t_{1}t_{2} = \frac{5 + m}{9}.

    AB = 8 \Leftrightarrow AB^{2} = 64.

    Suy ra 9\left( t_{2} - t_{1}\right)^{2} = 64 \Leftrightarrow 9\left\lbrack \left( t_{1} + t_{2}\right)^2- 4t_{1}t_{2} \right\rbrack = 64

    \Rightarrow 9.\left\lbrack 2^2 -4\left( \frac{5 + m}{9} \right) \right\rbrack = 64 \Leftrightarrow m = -12.

    Cách 2:

    Mặt cầu (S) có tâm I( - 2;3;0), R = \sqrt{13 - m}, m < 13.

    Đường thẳng (\Delta) qua M_{0}( - 2;0; - 3), có VTCP \overrightarrow{u} = (2;1;2)

    d = d\left( I;(\Delta) \right) = \frac{\left| \left\lbrack \overrightarrow{IM_{0}};\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 3

    Yêu cầu đề bài tương đương R^{2} = \frac{AB^{2}}{4} + d^{2} \Leftrightarrow 13 - m = 16 + 9 \Leftrightarrow m = - 12\ (n).

  • Câu 10: Vận dụng cao
    Tính giá trị của biểu thức

    Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2;1;3),B(6;5;5). Gọi (S) là mặt cầu đường kính AB. Mặt phẳng (P) vuông góc với đoạn AB tại H sao cho khối nón đỉnh A và đáy là hình tròn tâm H (giao của mặt cầu (S) và mặt phẳng (P)) có thể tích lớn nhất, biết rẳng (P):2x + by + cz + d = 0 với b;c;d\mathbb{\in Z}. Tính S = b +c + d.

    Hướng dẫn:

    Hình vẽ minh họa

    \overrightarrow{AB} = (4;4;2) = 2(2;2;1), \overrightarrow{AB} là vectơ pháp tuyến của mặt phẳng (P) suy ra phương trình mặt phẳng (P) có dạng 2x + 2y + z + d = 0.

    Gọi I là tâm mặt cầu thì I là trung điểm của AB suy ra I(4;3;4), bán kính mặt cầu R = \frac{AB}{2} = 3.

    Đặt IH = x suy ra HK = \sqrt{R^{2} - x^{2}} = \sqrt{9 - x^{2}}.

    Thể tích khối nón

    V = \frac{1}{3}IH.\pi.HK^{2} = \frac{1}{3}.\pi.\left( 9 - x^{2} \right)(3 + x)

    = \frac{1}{6}.\pi.(6 - 2x)(3 + x)(3 + x) \leq \frac{1}{6}.\pi\left( \frac{6 + 3 + 3}{3} \right)^{3}.

    Dấu bằng xảy ra khi 6 - 2x = 3 + x \Leftrightarrow x = 1.

    Ta có hệ: \left\{ \begin{matrix}d\left( A;(P) \right) = 4 \\d\left( I;(P) \right) = 1\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}\frac{|d + 9|}{3} = 4 \\\frac{|d + 18|}{3} = 1\end{matrix} \right.\Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} d = 3 \hfill \\ d = - 21 \hfill \\ \end{gathered} \right. \hfill \\ \left[ \begin{gathered} d = - 21 \hfill \\ d = - 15 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow d = - 21

    Vậy (P):2x + 2y + z -21 =0.

    Suy ra: b + c + d = - 18.

  • Câu 11: Vận dụng cao
    Tính bán kính đường tròn

    Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu (S):(x - 3)^{2} + (y - 3)^{2} + (z - 2)^{2} = 9 và ba điểm A(1;0;0),B(2;1;3),C(0;2; - 3). Biết rằng quỹ tích các điểm M thỏa mãn MA^{2} + 2\overrightarrow{MB}.\overrightarrow{MC} = 8 là đường tròn cố định, tính bán kính đường tròn này.

    Hướng dẫn:

    (S) có tâm I(3;3;2) bán kính R_{1} = 3.

    Gọi G là trọng tâm tam giác ABC, khi đó tọa độ G(1;1;0).

    \overrightarrow{GA} = (0; - 1;0);\overrightarrow{GB} = (1;0;3);\overrightarrow{GC} = ( - 1;1; - 3).

    MA^{2} + 2\overrightarrow{MB}.\overrightarrow{MC} = 8

    \Leftrightarrow 3MG^{2} + GA^{2} + 2\overrightarrow{MB}\left( \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} \right) + 2\overrightarrow{GB}\overrightarrow{GC} = 8

    \Leftrightarrow 3MG^{2} + 1 - 20 = 8 \Leftrightarrow MG = 3.

    Do đó, M nằm trên mặt cầu \left( S_{1} \right) tâm G bán kính R_{2} = 3 có phương trình (x - 1)^{2} + (y - 1)^{2} + z^{2} = 9.

    Vì IG = 2\sqrt{3} < R_{1} + R_{2} nên hai mặt cầu cắt nhau theo giao tuyến là đường tròn tâm H, bán kính r, nằm trên mặt phẳng x + y + z - 5 = 0.

    Từ đó suy ra r = \sqrt{R^{2} -d^2\left( I;(P) \right)} = \sqrt{6}.

  • Câu 12: Vận dụng cao
    Tính giá trị của biểu thức

    Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 16 và các điểm A(1;0;2),B( - 1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax + by + cz + 3 = 0. Tính T = a + b +c.

    Hướng dẫn:

    Mặt cầu (S) có tâm I(1; 2; 3) và bán kính R = 4.

    Vì IA = \sqrt{5} < R nên điểm A nằm bên trong mặt cầu. Suy ra (P) luôn cắt mặt cầu. Gọi r là bán

    kính đường tròn giao tuyến, ta có r = \sqrt{R^{2} - d^{2}} với d là khoảng cách từ I đến mặt phẳng (P).

    Diện tích hình tròn thiết diện nhỏ nhất khi và chỉ khi bán kính r nhỏ nhất, hay d lớn nhất.

    Gọi H là hình chiếu của I lên đường thẳng AB ta có d lớn nhất khi d = IH tức IH vuông góc với (P).

    Phương trình đường thẳng AB:\left\{ \begin{matrix} x = 1 - t \\ y = t \\ z = 2 \end{matrix} \right.\ (t\mathbb{\in R})

    Gọi H(1 - t;t;2). \overrightarrow{IH} = ( - t;t - 2; - 1).

    IH\bot AB \Leftrightarrow t + (t - 2) = 0 \Leftrightarrow t = 1. Suy ra H(0;1;2).

    Mặt phẳng (P) nhận \overrightarrow{IH} làm vectơ pháp tuyến và đi qua điểm A nên có phương trình

    - (x - 1) - y - (z - 2) = 0 \Leftrightarrow - x - y - z + 3 = 0.

    Vậy a + b + c =- 3.

  • Câu 13: Vận dụng cao
    Tính thể tích mặt cầu nội tiếp tứ diện

    Trong không gian ABCD cho tứ diện ABCD với điểm A(1;2;2), B( - 1;2; - 1), D(1;6; - 1) và D( - 1;6;2). Thể tích của mặt cầu nội tiếp tứ diện ABCD là

    Hướng dẫn:

    Ta có phương trình các mặt phẳng như sau:

    (ABC):6x - 3y - 4z+ 8 = 0

    (BCD):6x - 3y + 4z + 16 = 0

    (CDA):6x + 3y + 4z - 20 = 0

    (ABD):6x + 3y - 4z - 4 = 0

    Gọi I(a';b';c') là tâm và R là bán kính mặt cầu nội tiếp tứ diện DABC

    Do đó:

    I nằm cùng phái với A đối với (DBC) suy ra: 6a' - 3b' + 4c' + 16 > 0.

    I nằm cùng phía với B đối với (DAC) suy ra: 6a' + 3b' + 4c' - 20 < 0.

    I nằm cùng phía với C đối với (DAB) suy ra: 6a' + 3b' - 4c' - 4 > 0.

    I nằm cùng phía với D đối với (ABC) suy ra: 6a' - 3b' - 4c' + 8 < 0.

    Suy ra:

    \left\{ \begin{matrix} d\left( I;(DAB) \right) = d\left( I;(DAC) \right) \\ d\left( I;(DAB) \right) = d\left( I;(DBC) \right) \\ d\left( I;(DAB) \right) = d\left( I;(ABC) \right) \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} |6a' + 3b' - 4c' - 4| = |6a' + 3b' + 4c' - 20| \\ |6a' + 3b' - 4c' - 4| = |6a' - 3b' + 4c' + 16| \\ |6a' + 3b' - 4c' - 4| = |6a' - 3b' - 4c' + 8| \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} 6a' + 3b' - 4c' - 4 = - \left( 6a' + 3b' + 4c' - 20 \right) \\ 6a' + 3b' - 4c' - 4 = 6a' - 3b' + 4c' + 16 \\ 6a' + 3b' - 4c' - 4 = - \left( 6a' - 3b' - 4c' + 8 \right) \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} a' = 0 \\ b' = 4 \\ c' = \frac{1}{2} \end{matrix} \right.

    Suy ra: I\left( 0;4;\frac{1}{2} \right),R = \sqrt{\frac{36}{61}}

    Thể tích mặt cầu cần tìm là: V = \frac{4}{3}\pi R^{3} = \frac{288\pi\sqrt{61}}{3721}

    Cách khác: Sử dụng công thức nhanh.

    V_{ABCD} = \frac{1}{3}.r\left( S_{ABC} + S_{ABD} + S_{ADC} + S_{BCD} \right) (r là bán kính của mặt cầu nội tiếp)

    Ta có: \overrightarrow{AB} = ( - 2;0; - 3),\overrightarrow{AC} = (0;4; - 3) ,\overrightarrow{AD} = ( - 2;4;0),\overrightarrow{DB} = (0; - 4; - 3), \overrightarrow{DC} = (2;0; - 3).

    V_{ABCD} = \frac{1}{6}.\left| \left\lbrack \overrightarrow{AB};\overrightarrow{AC} \right\rbrack.\overrightarrow{AD} \right| = 8.

    S_{ABC} = \frac{1}{2}.\left| \left\lbrack \overrightarrow{AB};\overrightarrow{AC} \right\rbrack \right| = \sqrt{61}, S_{ADC} = \frac{1}{2}.\left| \left\lbrack \overrightarrow{AD};\overrightarrow{AC} \right\rbrack \right| = \sqrt{61}, S_{ABD} = \frac{1}{2}.\left| \left\lbrack \overrightarrow{AB};\overrightarrow{AD} \right\rbrack \right| = \sqrt{61},

    S_{BCD} = \frac{1}{2}.\left| \left\lbrack \overrightarrow{BD};\overrightarrow{DC} \right\rbrack \right| = \sqrt{61}.

    Ta có:

    V_{ABCD} = \frac{1}{3}.r\left( S_{ABC} + S_{ABD} + S_{ADC} + S_{BCD} \right)

    \Leftrightarrow 8 = \frac{1}{3}.r4\sqrt{61} \Leftrightarrow r = \sqrt{\frac{36}{21}}.

    Vậy: \mathbf{V =}\frac{\mathbf{4}}{\mathbf{3}}\mathbf{\pi}\mathbf{R}^{\mathbf{3}}\mathbf{=}\frac{\mathbf{288}\mathbf{\pi}\sqrt{\mathbf{61}}}{\mathbf{3721}}.

  • Câu 14: Vận dụng cao
    Tính tổng b và c

    Trong không gian Oxyz cho tứ diện với điểm A(1;2;2),B( - 1;2; - 1),C(1;6; - 1) và D( - 1;6;2). Biết mặt phẳng qua B, C và tâm mặt cầu nội tiếp tứ diện ABCD có một vectơ pháp tuyến là ( - 1;b;c). Tổng b + c là

    Hướng dẫn:

    Ta có phương trình các mặt phẳng như sau:

    (ABC): 6x - 3y - 4z + 8 = 0

    (BCD):6x - 3y + 4z + 16 = 0

    (CDA):6x + 3y + 4z - 20 = 0

    (ABD):6x + 3y - 4z - 4 = 0

    Gọi I(a';b';c') là tâm mặt cầu nội tiếp tứ diện DABC

    Do đó:

    I nằm cùng phái với A đối với (DBC) suy ra: 6a' - 3b' + 4c' + 16 > 0.

    I nằm cùng phía với B đối với (DAC) suy ra: 6a' + 3b' + 4c' + 20 < 0.

    I nằm cùng phía với C đối với (DAB) suy ra: 6a' + 3b' - 4c' - 4 > 0.

    I nằm cùng phía với D đối với (ABC) suy ra: 6a' - 3b' - 4c' + 8 < 0.

    Suy ra:

    \left\{ \begin{matrix} d\left( I;(DAB) \right) = d\left( I;(DAC) \right) \\ d\left( I;(DAB) \right) = d\left( I;(DBC) \right) \\ d\left( I;(DAB) \right) = d\left( I;(ABC) \right) \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} |6a' + 3b' - 4c' - 4| = |6a' + 3b' + 4c' - 20| \\ |6a' + 3b' - 4c' - 4| = |6a' - 3b' + 4c' + 16| \\ |6a' + 3b' - 4c' - 4| = |6a' - 3b' - 4c' + 8| \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} 6a' + 3b' - 4c' - 4 = - \left( 6a' + 3b' + 4c' - 20 \right) \\ 6a' + 3b' - 4c' - 4 = 6a' - 3b' + 4c' + 16 \\ 6a' + 3b' - 4c' - 4 = - \left( 6a' - 3b' - 4c' + 8 \right) \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} a' = 0 \\ b' = 4 \\ c' = \frac{1}{2} \end{matrix} \right.

    Suy ra: I\left( 0;4;\frac{1}{2} \right),\overrightarrow{BI} = \left( 1;2;\frac{3}{1} \right),\overrightarrow{BC} = (2;4;0)

    \left\lbrack \overrightarrow{BI},\overrightarrow{BC} \right\rbrack = ( - 3;3;0)cùng phương với \overrightarrow{n} = ( - 1;1;0).

    Suy ra (BCI) có một VTPT là \overrightarrow{n} = ( - 1;1;0) = ( - 1;b;c).

    Vậy b + c = 1.

  • Câu 15: Vận dụng cao
    Xác định số điểm A thỏa mãn yêu cầu

    Trong không gian Oxyz, cho mặt cầu (S):x^{2} + y^{2} + \left( z + \sqrt{2} \right)^{2} = 3. Có tất cả bao nhiêu điểm A(a;b;c) (a;b;c là các số nguyên) thuộc mặt phẳng (Oxy) sao cho có ít nhất hai tiếp tuyến của (S) đi qua A và hai tiếp tuyến đó vuông góc với nhau?

    Hướng dẫn:

    Do A(a;b;c) thuộc mặt phẳng (Oxy) nên A(a;b;0).

    Nhận xét: Nếu từ A kẻ được ít nhất 2 tiếp tuyến vuông góc đến mặt cầu khi và chỉ khi R \leq IA \leq R\sqrt{2}

    \Leftrightarrow 3 \leq a^{2} + b^{2} + 2 \leq 6 \Leftrightarrow 1 \leq a^{2} + b^{2} \leq 4

    Tập các điểm thỏa đề là các điểm nguyên nằm trong hình vành khăn (kể cả biên), nằm trong mặt phẳng (Oxy), tạo bởi 2 đường tròn đồng tâm O(0;0;0) bán kính lần lượt là 1 và 2.

    Nhìn hình vẽ ta có 12 điểm thỏa mãn yêu cầu bài toán.

  • Câu 16: Vận dụng cao
    Xác định số mặt phẳng

    Trong không gian Oxyz, cho 3 điểm A(3;7;1),B(8;3;8) và C(3;3;0). Gọi \left( S_{1} \right) là mặt cầu tâm A bán kính bằng 3 và \left( S_{2} \right) là mặt cầu tâm B bán kính bằng 6. Hỏi có tất cả bao nhiêu mặt phẳng đi qua C và tiếp xúc đồng thời với cả hai mặt cầu \left( S_{1} \right),\left( S_{2} \right)?

    Hướng dẫn:

    Phương trình mặt phẳng qua C có dạng (P):m(x - 3) + n(y - 3) + pz = 0,m^{2} + n^{2} + p^{2} > 0.

    Mặt phẳng (P) tiếp xúc \left( S_{1} \right) ta có |4n + p| = 3\sqrt{m^{2} + n^{2} + p^{2}} (1)

    Mặt phẳng (P) tiếp xúc \left( S_{2} \right) ta có |5m + 8p| = 6\sqrt{m^{2} + n^{2} + p^{2}} (2)

    Từ đây ta có phương trình |5m + 8p| = 2|4n + p| \Leftrightarrow \left\lbrack \begin{matrix} 5m = 8n - 6p\ \ \ (3) \\ 5m = - 8n - 10p\ \ \ (4) \end{matrix} \right.

    Từ (1), (3) ta có:

    (4n + p)^{2} = 9\left\lbrack \left( \frac{8n - 6p}{5} \right)^{2} + n^{2} + p^{2} \right\rbrack

    \Leftrightarrow 401n^{2} - 1064np + 524p^{2} = 0 \Leftrightarrow \left\lbrack \begin{matrix} n = 2p \\ n = \frac{262}{401}p \end{matrix} \right.

    Trường hợp này ta tìm được hai mặt phẳng:

    \left( P_{1} \right):2x + 2y + z - 12 = 0

    \left( P_{2} \right):62x - 262y - 101z + 600 = 0

    Từ (1); (4) ta có:

    (4n + p)^{2} = 9\left\lbrack \left( \frac{8n + 10p}{5} \right)^{2} + n^{2} + p^{2} \right\rbrack

    \Leftrightarrow 401n^{2} + 1240np + 1100p^{2} = 0 \Leftrightarrow n = p = 0

    Trường hợp này không có mặt phẳng nào.

  • Câu 17: Vận dụng cao
    Chọn đáp án đúng

    Trong không gian Oxyz, cho 3 điểm A(0;0;1),B(0;2;2) và C(3; - 1; - 1). Gọi \left( S_{1} \right) là mặt cầu tâm A bán kính bằng 1 và \left( S_{2} \right) là mặt cầu tâm B bán kính bằng 3. Hỏi có tất cả bao nhiêu mặt phẳng đi qua C và tiếp xúc đồng thời với cả hai mặt cầu \left( S_{1} \right),\left( S_{2} \right)?

    Hướng dẫn:

    Phương trình mặt phẳng qua C có dạng (P):m(x - 3) + n(y + 1) + p(z + 1) = 0,m^{2} + n^{2} + p^{2} > 0.

    Mặt phẳng (P) tiếp xúc \left( S_{1} \right) ta có | - 3m + n + 2p| = \sqrt{m^{2} + n^{2} + p^{2}} (1)

    Mặt phẳng (P) tiếp xúc \left( S_{2} \right) ta có | - 3m + 3n + 3p| = 3\sqrt{m^{2} + n^{2} + p^{2}} (2)

    Từ đây ta có phương trình

    | - 3m + 3n + 3p| = 3| - 3m + n + 2p|

    \Leftrightarrow \left\lbrack \begin{matrix} p = 2m\ \ \ (3) \\ 3p = 4m - 2n\ \ \ (4) \end{matrix} \right.

    Từ (1), (3) ta có:

    |m + n| = \sqrt{5m^{2} + n^{2}} \Leftrightarrow \left\lbrack \begin{matrix} m = 0 \\ n = 2m \end{matrix} \right.

    Trường hợp này ta tìm được hai mặt phẳng:

    \left( P_{1} \right):y + 1 = 0

    \left( P_{2} \right):x + 2y + 2z + 1 = 0

    Từ (1); (4) ta có:

    4m^{2} - 3mn + 2n^{2} = 0 \Leftrightarrow m - n = 0

    Trường hợp này không có mặt phẳng nào.

  • Câu 18: Vận dụng cao
    Chọn đáp án đúng

    Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0;8;2) và mặt cầu (S):(x - 5)^{2} + (y + 3)^{2} + (z - 7)^{2} = 72 và điểm B(9; - 7;23). Viết phương trình mặt phẳng (P) đi qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử \overrightarrow{n}(1;m;n) là một vectơ pháp tuyến của (P). Khi đó

    Hướng dẫn:

    Giả sử mặt phẳng (P) có dạng:

    a(x - 0) + b(y - 8) + c(z - 2) = 0;\left( a^{2} + b^{2} + c^{2} \neq 0 \right).

    \Leftrightarrow ax + by + cz - 8b - 2c = 0

    Mặt cầu (S) có tâm I(5; - 3;7) và bán kính R = 6\sqrt{2}

    Điều kiện tiếp xúc:

    d\left( I;(P) \right) = 6\sqrt{2} \Leftrightarrow \frac{|5a- 3b + 7c - 8b - 2c|}{\sqrt{a^{2} + b^{2} + c^{2}}} = 6\sqrt{2} \Leftrightarrow \frac{|5a - 11b + 5c|}{\sqrt{a^{2} + b^{2} + c^{2}}} = 6\sqrt{2}(*).

    Mà d\left( B;(P) \right) = \frac{|9a - 7b+ 23c - 8b - 2c|}{\sqrt{a^{2} + b^{2} + c^{2}}}= \frac{|9a - 15b +21c|}{\sqrt{a^{2} + b^{2} + c^{2}}}

    = \frac{\left| 5a - 11b + 5c + 4(a - b +4c) \right|} {\sqrt{a^{2} + b^{2} + c^{2}}}

    \leq \frac{|5a - 11b + 5c|}{\sqrt{a^{2} + b^{2} + c^{2}}} + 4.\frac{|a - b + 4c|}{\sqrt{a^{2} + b^{2} + c^{2}}}

    \leq 6\sqrt{2} + 4.\frac{\sqrt{1^{2} + ( - 1)^{2} + 4^{2}}.\sqrt{a^{2} + b^{2} + c^{2}}}{\sqrt{a^{2} + b^{2} + c^{2}}} = 18\sqrt{2}

    Dấu bằng xảy ra khi \frac{a}{1} = \frac{b}{- 1} = \frac{c}{4}

    Chọn a = 1;b = - 1;c = 4 thỏa mãn (*).

    Khi đó (P):x - y + 4z = 0

    Suy ra m = - 1;n = 4 \Rightarrow mn = - 4 .

  • Câu 19: Vận dụng cao
    Tính độ dài đoạn thẳng MN

    Trong không gian với hệ trục tọa độ Oxyzcho đường thẳng d:\frac{x - 2}{2} = \frac{y}{- 1} = \frac{z}{4} và mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 1)^{2} = 2. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng

    Hướng dẫn:

    Hình vẽ minh họa

    Từ (S) Tâm I(1;2;1) và bán kính R = \sqrt{2}

    Từ d Vectơ \overrightarrow{u} = (2; - 1;4)

    Hạ \overrightarrow{u} = (2; - 1;4) \Rightarrow H(2 + 2t; - t;4t)

    \Rightarrow \overrightarrow{IH}.\overrightarrow{u} = \overrightarrow{0}

    \Leftrightarrow (2t + 1).2 + ( - 1).( - 2 - t) + (4t - 1).4 = 0

    \Leftrightarrow t = 0 \Leftrightarrow H(2;0;0)

    Xét tam giác \Delta IHM vuông tại M ta có:

    MH^{2} = IH^{2} - IM^{2} = 62 = 4 \Rightarrow MH = 2.

    Ta có \frac{1}{MK^{2}} = \frac{1}{MH^{2}} + \frac{1}{MI^{2}} = \frac{1}{4} + \frac{1}{2} = \frac{3}{4} \Rightarrow MK = \frac{2}{\sqrt{3}}.

    \Rightarrow MN = 2MK = \frac{4}{\sqrt{3}}.

  • Câu 20: Vận dụng cao
    Tính khoảng cách từ điểm đến mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho A(a;0;0),B(0;b;0),C(0;0;c) với a;b;c dương. Biết A;B;C di động trên các tia Ox;Oy,Oz sao cho a + b + c = 2. Biết rằng khi a;b;c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P).

    Hướng dẫn:

    +) Gọi (\alpha),(\beta),(\gamma) lần lượt là mặt phẳng trung trực của các đoạn OA;OB;OC.

    Suy ra (\alpha):x - \frac{a}{2} = 0,(\beta):y - \frac{a}{2} = 0,(\gamma):z - \frac{a}{2} = 0

    +) Gọi I là tâm mặt cầu ngoại tiếp tứ diện O.ABCthì I = (\alpha) \cap (\beta) \cap (\gamma).

    Tìm được I\left( \frac{a}{2};\frac{a}{2};\frac{a}{2} \right)

    +)a + b + c = 2 \Leftrightarrow \frac{a}{2} + \frac{b}{2} + \frac{c}{2} = 1, do đó I \in (P):x+y + z = 1

    +) d\left( M;(P) \right) = \frac{|2016 - 1|}{\sqrt{3}} = \frac{2015}{\sqrt{3}}.

  • Câu 21: Vận dụng cao
    Tính chu vi của đường tròn

    Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P):x - y - z + 3 = 0 và hai điểm M( - 1;1; - 1),N(3; - 3;3). Mặt cầu (S) đi qua hai điểm M,N và tiếp xúc với (P) tại C. Biết rằng C luôn thuộc một đường tròn cố định. Tính chu vi của đường tròn đó.

    Hướng dẫn:

    Ta có MN đi qua M( - 1;1; - 1), nhận \frac{1}{4}\overrightarrow{MN} = \frac{1}{4}(4; - 4;4) = (1; - 1;1) là một vecto chỉ phương nên MN:\left\{ \begin{matrix} x = - 1 + t \\ y = 1 - t \\ z = - 1 + t \end{matrix} \right.\ ;\left( t\mathbb{\in R} \right).

    Thay \left\{ \begin{matrix} x = - 1 + t \\ y = 1 - t \\ z = - 1 + t \end{matrix} \right.vào (P) ta được - 1 + t + 1 + t + 1 - t + 3 = 0 \Leftrightarrow t = 4

    Tọa độ điểm D(3;3;3) là giao điểm của của MN và (P). Do đó theo tính chất của phương tích ta được DM.DN = DI^{2} - R^{2}.

    Mặt khác vì DC là tiếp tuyến của mặt cầu (S) cho nên DC^{2} = DI^{2} - R^{2}.

    Do vậy DC^{2} = DM.DN = 36 \Rightarrow DC = 6 (là một giá trị không đổi).

    Vậy C luôn thuộc một đường tròn cố định tâm D với bán kính R = 6 suy ra chu vi của đường tròn là 12\pi.

  • Câu 22: Vận dụng cao
    Tính thể tích khối tứ diện

    Trong không gian với hệ tọa độ Oxyz cho các điểm A(a;0;0),B(0;b;0),C(0;0;c) trong đó a > 0,b > 0,c > 0 và \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7. Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = \frac{72}{7} Tính thể tích của khối tứ diện O.ABC

    Hướng dẫn:

    +) Ta có (ABC):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1

    +) Mặt cầu (ABC):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 có tâm I(1;2;3) và bán kính R = \sqrt{\frac{72}{7}}

    +) Mặt phẳng (ABC) tiếp xúc với (S) \Leftrightarrow d\left( I;(ABC) \right) = R \Leftrightarrow \frac{\left| \frac{1}{a} + \frac{2}{b} + \frac{3}{c} - 1 \right|}{\sqrt{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} = \sqrt{\frac{72}{7}}.

    +) Áp dụng BĐT Bunhiacopski ta có:

    \left( 1^{2} + 2^{2} + 3^{2} \right)\left( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \right) \geq \left( \frac{1}{a} + \frac{2}{b} + \frac{3}{c} \right)^{2} = 7^{2}

    \Rightarrow \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \geq \frac{7}{2}

    +) Dấu xảy ra \left. \ \begin{matrix} \frac{1}{\frac{1}{a}} = \frac{2}{\frac{1}{b}} = \frac{3}{\frac{1}{c}} \\ \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7 \end{matrix} \right\} \Rightarrow \left\{ \begin{matrix} a = 2 \\ b = 1 \\ c = \frac{2}{3} \end{matrix} \right. khi đó V_{OABC} = \frac{1}{6}abc = \frac{2}{9}

  • Câu 23: Vận dụng cao
    Tính bán kính mặt cầu

    Trong không gian Oxyz, cho ba điểm A(2;0;0),B(0;4;0),C(0;0;6), điểm M thay đổi trên mặt phẳng (ABC), N là điểm trên tia OM sao cho OM.ON = 12. Biết khi M thay đổi thì điểm N luôn nằm trên mặt cầu cố định. Tính bán kính mặt cầu đó

    Hướng dẫn:

    Giả sử N(x;y;z) \Rightarrow ON = \sqrt{x^{2} + y^{2} + z^{2}}.

    Do O, M, N thẳng hàng và N thuộc tia ON nên suy ra:

    OM.ON = 12 \Leftrightarrow\overrightarrow{OM} = \frac{12}{x^{2} + y^{2} +z^2}.\overrightarrow{ON}

    Do N \in (ABC) \Rightarrow 6x + 3y + 2z = x^{2} + y^{2} + z^{2}

    \Leftrightarrow (x - 3)^{2} + \left( y -\frac{3}{2} \right)^2 + (z - 1)^{2} = \frac{49}{4}

    Vậy N thuộc mặt cầu cố định bán kính R = \frac{7}{2}.

  • Câu 24: Vận dụng cao
    Tính tổng diện tích của ba đường tròn tương ứng

    Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S):(x - 1)^{2} + (y + 1)^{2} + (z - 2)^{2} = 16 và điểm A(1;2;3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.

    Hướng dẫn:

    Cách 1:

    Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là (P),(Q),(R) .

    Với điểm I bất kỳ, hạ II_{1};II_{2};II_{3} lần lượt vuông góc với ba mặt phẳng (P),(Q),(R) thì ta luôn có: IA^{2} = I{I_{1}}^{2} + I{I_{2}}^{2} + I{I_{3}}^{2}\ \ \ (1).

    Thật vậy, ta chọn hệ trục tọa độ Oxyz vớiO \equiv A, ba trục Ox,Oy,Oz lần lượt là ba giao tuyến của ba mặt phẳng (P),(Q),(R).

    Khi đó tọa độ I(a;b;c) thì:

    IA^{2} = a^{2} + b^{2} + c^{2} = d^{2}\left( A;(Iyz) \right) + d^{2}\left( A;(Ixz) \right) + d^{2}\left( A;(Ixy) \right)

    hay IA^{2} = I{I_{1}}^{2} + I{I_{2}}^{2} + I{I_{3}}^{2}.

    Vậy (1) được chứng minh.

    Áp dụng giải bài :

    Mặt cầu (S) có tâm I(1; - 1;2) và có bán kính r = 4.

    \overrightarrow{IA}(0;3;1) \Rightarrow IA = \sqrt{10}.

    Giả sử ba mặt mặt phẳng cùng đi qua A đôi một vuông góc với nhau là (P),(Q),(R) và cắt mặt cầu (S) theo ba đường tròn lần lượt là: \left( C_{1} \right),\left( C_{2} \right),\left( C_{3} \right)

    Gọi I_{1};I_{2};I_{3} và r_{1};r_{2};r_{3} lần lượt là tâm và bán kính của \left( C_{1} \right),\left( C_{2} \right),\left( C_{3} \right)

    Khi đó: II_{1}\bot(P) \Leftrightarrow I{I_{1}}^{2} + {r_{1}}^{2} = r^{2} \Leftrightarrow {r_{1}}^{2} = r^{2} - I{I_{1}}^{2}.

    Tương tự có: {r_{2}}^{2} = r^{2} - I{I_{2}}^{2};{r_{3}}^{2} = r^{2} - I{I_{3}}^{2}.

    Theo nhận xét ở trên ta có: IA^{2} = I{I_{1}}^{2} + I{I_{2}}^{2} + I{I_{3}}^{2}

    Ta có tổng diện tích các đường tròn là :

    S = \pi\left( {r_{1}}^{2} + {r_{2}}^{2} + {r_{3}}^{2} \right) = \pi\left( r^{2} - I{I_{1}}^{2} + r^{2} - I{I_{2}}^{2} + r^{2} - I{I_{3}}^{2} \right)

    = \pi\left\lbrack 3r^{2} - \left( I{I_{1}}^{2} + I{I_{2}}^{2} + I{I_{3}}^{2} \right) \right\rbrack

    = \pi\left( 3r^{2} - IA^{2} \right) = 38\pi.

    Cách 2:

    Đặt biệt hóa: Giả sử có 3 đường tròn \left( S_{1} \right),\left( S_{2} \right),\left( S_{3} \right); như hình bên trong đó \left( S_{1} \right),\left( S_{2} \right) đều là đường tròn lớn có bán kính là 4.

    I(1; - 1;2),A(1;2;3) suy ra IA = \sqrt{10};R = 4.

    Suy ra bán kính hình tròn \left( S_{3} \right) là r = \sqrt{16 - 10} = \sqrt{6}

    Tổng diện tích các hình tròn là: \pi.4^{2} + \pi.4^{2} + \pi.\left( \sqrt{6} \right)^{2} = 38\pi.

  • Câu 25: Vận dụng cao
    Tìm giá trị lớn nhất của biểu thức

    Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S):x^{2} + y^{2} + z^{2} - 2x + 4y + 4z = 0 và điểmM(1;2; - 1). Một đường thẳng thay đổi qua M cắt (S) tại hai điểm A; B. Tìm giá trị lớn nhất của tổng MA + MB.

    Hướng dẫn:

    Mặt cầu (S) có tâm I(1; - 2; - 2) và bán kính R = 3. Trong khi IM = \sqrt{17} > 3 nên M nằm ngoài hình cầu (S).

    Gọi H là trung điểm của AB, có M nằm trên đường AB và nằm ngoài đoạn AB nên có MA + MB = 2MH.

    Mặt khác, tam giác IHM vuông tại H nên HM \leq MI. Vậy MA + MB \leq 2\sqrt{17}.

    Đẳng thức xảy ra khi đường thẳng qua M và tâm I của mặt cầu, tức AB lúc này là đường kính của mặt cầu.

    Vậy giá trị lớn nhất của tổng MA + MB là 2\sqrt{17}.

0/25
25 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (100%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
23 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Chuyên đề Toán 12
Xem thêm