Tổng quan phương trình mặt cầu trong không gian Oxyz
Cách viết phương trình mặt cầu Toán 12
Trong hình học không gian Oxyz, phương trình mặt cầu là một trong những nội dung quan trọng của chương trình Toán 12. Bài học giúp học sinh hiểu rõ bản chất của mặt cầu, các yếu tố đặc trưng như tâm, bán kính, cũng như cách xác định phương trình mặt cầu trong Oxyz dựa trên điều kiện hình học cho trước.
Bài viết “Tổng quan phương trình mặt cầu trong không gian Oxyz” không chỉ hệ thống hóa kiến thức lý thuyết cơ bản mà còn cung cấp ví dụ minh họa, bài tập và đáp án chi tiết, giúp học sinh dễ dàng ghi nhớ công thức, rèn luyện kỹ năng giải bài tập hình học không gian và đạt kết quả cao trong các kỳ thi THPT Quốc gia môn Toán.
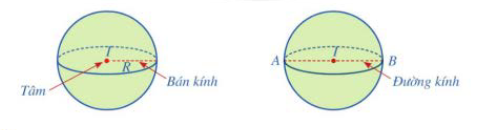
A. Định nghĩa Mặt cầu
Cho trước điểm 
\(I\) và số dương \(R\). Mặt cầu tâm \(I\) bán kính \(R\) là tập hợp tất cả các điểm trong không gian cách điểm \(I\) một khoảng bằng \(R\).
Nhận xét:
• Điểm M thuộc mặt cầu tâm I bán kính R khi và chỉ khi \(IM = R\).
• Điểm M nằm trong mặt cầu tâm I bán kính R khi và chỉ khi \(IM < R\).
• Điểm M nằm ngoài mặt cầu tâm I bán kính R khi và chỉ khi \(IM > R\).
Ví dụ 1. Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu tâm \(I(0;1; - 2)\) bán kính 3. Các điểm \(M(5; - 3;2),N( - 1;1; - 3),P(2;2;0)\) nằm trong nằm trên hay nằm ngoài mặt cầu đó?
Hướng dẫn giải
Do \(IM = \sqrt{(5 - 0)^{2} + ( - 3 -
1)^{2} + \left( 2 - ( - 2) \right)^{2}} = \sqrt{57} > 3\) nên điểm \(M(5; - 3;2)\) nằm ngoài mặt cầu đó.
\(IN = \sqrt{( - 1 - 0)^{2} + (1 - 1)^{2} +
\left( - 3 - ( - 2) \right)^{2}} = \sqrt{2} < 3\) nên điểm \(N( - 1;1; - 3)\) nằm trong mặt cầu đó.
\(IP = \sqrt{(2 - 0)^{2} + (2 - 1)^{2} +
\left( 0 - ( - 2) \right)^{2}} = \sqrt{9} = 3\) nên điểm \(P(2;2;0)\) nằm trên mặt cầu đó.
Ví dụ 2. Trong không gian \(Oxyz\) cho điểm \(I(2;3;4)\) và mặt cầu tâm I đi qua điểm \(A(1;2;3)\). Tính bán kính \(R\) của mặt cầu đó?
Hướng dẫn giải
Bán kính mặt cầu là \(R = IA = \sqrt{(1 -
2)^{2} + (2 - 3)^{2} + (3 - 4)^{2}} = \sqrt{3}\).
B. Phương trình mặt cầu trong không gian Oxyz
Phương trình mặt cầu tổng quát
Trong không gian \(Oxyz\), cho mặt cầu tâm \(I(a;b;c)\) bán kính \(R\) có phương trình là: \((x - a)^{2} + (y - b)^{2} + (z - c)^{2} =
R^{2}\).
Phương trình mặt cầu dạng khai triển
Ta có thể viết phương trình đó về dạng: \(x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d =
0\) với \(d = a^{2} + b^{2} + c^{2} -
R^{2}\).
Vậy mỗi mặt cầu đều có phương trình dạng: \(x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d =
0\).
Ngược lại, xét phương trình có dạng: \(x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d =
0\) là phương trình một mặt cầu khi và chỉ khi \(a^{2} + b^{2} + c^{2} - d > 0\).
Điều kiện để phương trình là phương trình mặt cầu
Nếu \(a^{2} + b^{2} + c^{2} - d >
0\) thì phương trình đó xác định mặt cầu tâm \(I(a;b;c)\) và bán kính \(R = \sqrt{a^{2} + b^{2} + c^{2} - d}\).
C. Bài tập minh họa về phương trình mặt cầu có đáp án
Ví dụ 1. Viết phương trình mặt cầu, biết
a) Tâm \(I(1; - 1; - 3)\) bán kính \(R = 5\).
b) Tâm \(I(2; - 1; - 1)\) và đi qua điểm \(A(1;2;3)\).
Hướng dẫn giải
a) Phương trình của mặt cầu tâm \(I(1;2;3)\) bán kính \(R = 5\) là:
\((x - 1)^{2} + (y + 1)^{2} + (z + 3)^{2} =
25\).
b) Bán kính mặt cầu là:
\(R = IA = \sqrt{(1 - 2)^{2} + (2 + 1)^{2}
+ (3 + 1)^{2}} = \sqrt{26}\)
Phương trình của mặt cẩu tâm \(I(2; - 1; -
1)\) bán kính \(R = \sqrt{26}\) là: \((x - 2)^{2} + (y + 1)^{2} + (z + 1)^{2}
= 26\).
Ví dụ 2. Mỗi phương trình sau có là phương trình mặt cầu hay không? Vì sao?
a) \(3x^{2} + 2y^{2} + z^{2} - 2x - 2y + 2z
+ 1 = 0\).
b) \(x^{2} + y^{2} - 2x + 6y - 8z - 3 =
0\).
Hướng dẫn giải
a) Phương trình \(3x^{2} + 2y^{2} + z^{2} -
2x - 2y + 2z + 1 = 0\) không phải là phương trình của một mặt cầu vì các hệ số của \(x^{2}\) và \(y^{2}\) khác nhau.
b) Phương trình \(x^{2} + y^{2} - 2x + 6y -
8z - 3 = 0\) không phải là phương trình của một mặt cầu vì không có biểu thức \(y^{2}\).
Ví dụ 3. Phương trình nào sau đây là phương trình của một mặt cầu? Tìm tâm và bán kính của mặt cầu (nếu có).
a) \(x^{2} + y^{2} + z^{2} - 6x + 8y - 2z +
10 = 0\).
b) \(2x^{2} + 2y^{2} + 2z^{2} + 12x + 4y -
8z + 20 = 0\).
Hướng dẫn giải
a) Ta có: \(x^{2} + y^{2} + z^{2} - 6x + 8y
- 2z + 10 = 0\)
\(\Leftrightarrow x^{2} + y^{2} + z^{2} -
2.3.x + 2.4.y - 2.1.z + 10 = 0\)
\(\Leftrightarrow (x - 3)^{2} + (y + 4)^{2}
+ (z - 1)^{2} = 16\).
Vậy phương trình đã cho là phương trình mặt cầu tâm \(I(3; - 4;1)\) bán kính \(R = \sqrt{16} = 4\).
b) Ta có: \(2x^{2} + 2y^{2} + 2z^{2} + 12x
+ 4y - 8z + 20 = 0\)
\(\begin{matrix}
\Leftrightarrow x^{2} + y^{2} + z^{2} + 6x + 2y - 4z + 10 = 0 \\
\Leftrightarrow x^{2} + y^{2} + z^{2} + 2.3.x + 2.1.y - 2.2.z + 10 = 0
\end{matrix}\)
\(\Leftrightarrow (x + 3)^{2} + (y + 1)^{2}
+ (z - 2)^{2} = 4\).
Vậy phương trình đã cho là phương trình mặt cầu tâm \(I( - 3; - 1;2)\) bán kính \(R = \sqrt{4} = 2\).
--------------------------------------------------------------
Qua chuyên đề phương trình mặt cầu trong không gian Oxyz, học sinh lớp 12 có thể nắm vững lý thuyết và áp dụng linh hoạt vào các dạng bài tập khác nhau. Hãy tiếp tục ôn luyện với các chuyên đề Toán 12 có đáp án khác như mặt phẳng, đường thẳng, hình chóp và mặt trụ, để củng cố kiến thức hình học không gian, sẵn sàng cho kỳ thi tốt nghiệp THPT.
