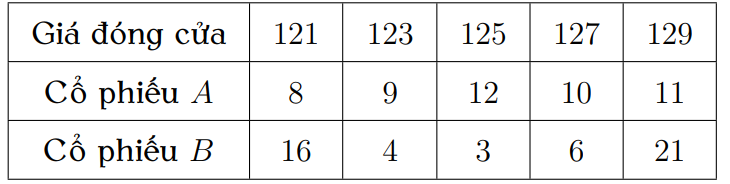
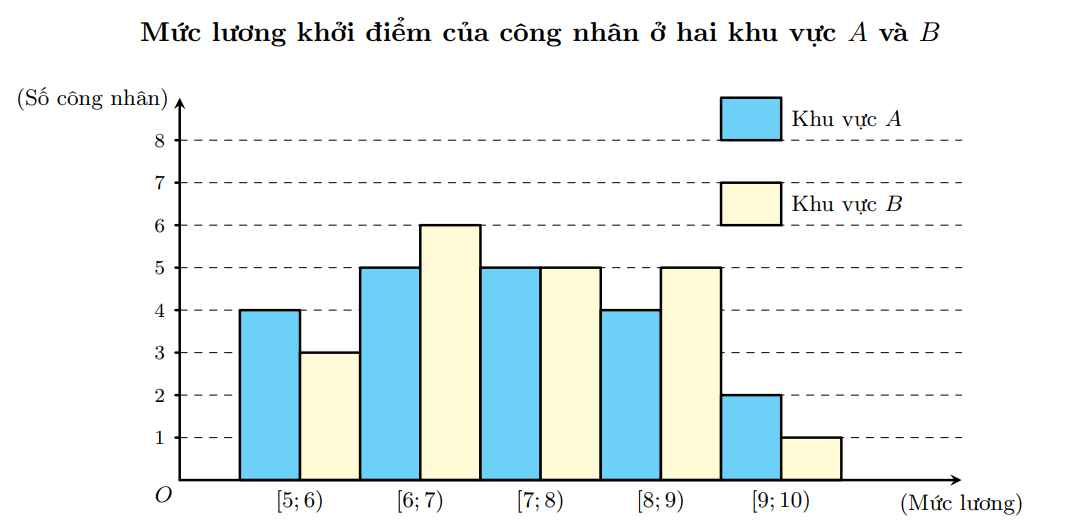
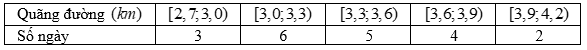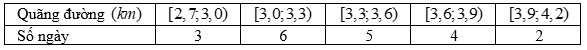Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik , bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

Phương sai của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?
Ta có:
|
Giá trị đại diện |
9 |
11 |
13 |
15 |
17 |
|
Số lần |
4 |
_6 |
8 |
4 |
3 |
Số trung bình:
Phương sai: