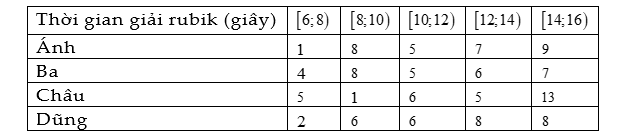
Một ý nghĩa của khoảng tứ phân vị là
Ý nghĩa của khoảng tứ phân vị:
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị bất thường của mẫu đó.
- - Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết giá trị bất thường của mẫu số liệu và nó không bị ảnh hưởng bởi các giá trị bất thường đó.