Tìm m để phương trình sau có nghiệm lớp 12
Tìm tham số m để phương trình có nghiệm
Tìm m để phương trình sau có nghiệm lớp 12 là một dạng toán quen thuộc trong chương trình Giải tích lớp 12, đặc biệt khi kết hợp với tính đơn điệu của hàm số để giải quyết bài toán chứa tham số. Đây là phần kiến thức trọng tâm, thường xuyên xuất hiện trong đề thi tốt nghiệp THPT. Bài viết sẽ giúp bạn hiểu rõ cách vận dụng tính đồng biến, nghịch biến để phân tích điều kiện có nghiệm của phương trình và tìm giá trị tham số m phù hợp.
A. Bài tập minh họa tìm m để phương trình có nghiệm
Bài 1: Tìm m để phương trình sau có hai nghiệm phân biệt:
\((m + 1)\sqrt{x^{2} + 2x + 2} + m =
2x^{2} + 4x + 19,(x\mathbb{\in R})\ \ \ \ \ (1)\)
Hướng dẫn giải
Đặt \(t = \sqrt{x^{2} + 2x + 2}\) ; điều kiện: \(t \geq 1\).
Ta có: \(t = \sqrt{x^{2} + 2x + 2}
\Leftrightarrow x^{2} + 2x + 2 = t^{2} \Leftrightarrow x^{2} + 2x + 2 -
t^{2} = 0\) (2)
Pt (2) có hai nghiệm phân biệt \(\Leftrightarrow t \in ( - \infty; - 1) \cup (1; +
\infty)\). Vậy \(t > 1\).
Thay vào phương trình ta được: \((m + 1)t +
m = 2t^{2} + 15 \Leftrightarrow m = \frac{2t^{2} - t + 15}{t +
1}\) (3)
Đặt \(\left\{ \begin{matrix}
y = \frac{2t^{2} - t + 15}{t + 1}\ \ \ \ (C) \\
y = m\ \ \ \ \ (d)
\end{matrix} \right.\). Ta có: Số giao điểm của (C) và (d) là số nghiệm phương trình (3).
Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có đúng 1 nghiệm\(t > 1\).
Xét hàm số \(y = 2t - 3 + \frac{18}{t +
1};(t \in \lbrack 1; + \infty))\) ; \(y' = 2 - \frac{18}{(t + 1)^{2}}\).
Cho \(y' = 0 \Leftrightarrow t = 2
\Rightarrow y = 7;\lim_{x \rightarrow + \infty}y = +
\infty\).
Bảng biến thiên
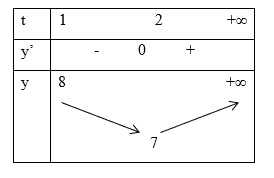
Vậy phương trình (1) có hai nghiệm phân biệt \(\Leftrightarrow \left\lbrack \begin{matrix}
m > 8 \\
m = 7
\end{matrix} \right.\).
Bài 2: Tìm các giá trị của tham số m để phương trình:\(\sqrt{x} + \sqrt{9 - x} = \sqrt{- x^{2} + 9x +
m}\) có nghiệm.
Hướng dẫn giải
Điều kiện: \(0 \leq x \leq 9\)
PT (1) \(\Leftrightarrow x + 9 - x +
2\sqrt{x(9 - x)} = - x^{2} + 9x + m\)
\(\Leftrightarrow 9 + 2\sqrt{- x^{2} + 9x}
= - x^{2} + 9x + m\) (2)
Đặt \(t = \sqrt{- x^{2} + 9x}\)
Ta có: \(t' = \frac{- 2x + 9}{2\sqrt{-
x^{2} + 9x}}\); \(t' = 0
\Leftrightarrow x = \frac{9}{2}\)
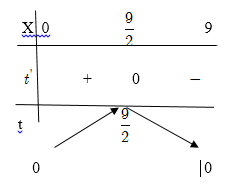
Do đó : \(0 \leq t \leq
\frac{9}{2}\)
Phương trình (2) trở thành \(9 + 2t = t^{2}
+ m \Leftrightarrow - t^{2} + 2t + 9 = m\) (3)
Xét hàm số \(f(t) = - t^{2} + 2t +
9\), \(0 \leq t \leq
\frac{9}{2}\)
Ta có : \(f'(t) = - 2t + 2\ \ ;\ \
f'(t) = 0 \Leftrightarrow t = 1\)
Bảng biến thiên:
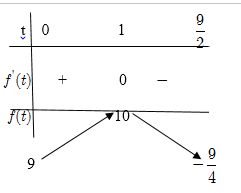
Phương trình (1) có nghiệm \(x \in \lbrack
0;9\rbrack \Leftrightarrow\) phương trình (3) có nghiệm \(t \in \left\lbrack 0;\frac{9}{2}
\right\rbrack\)
\(\Leftrightarrow - \frac{9}{4} \leq m
\leq 10\)
Bài 3: Tìm các giá trị của tham số m để phương trình sau có nghiệm
\(3\sqrt{x - 1} + m\sqrt{x + 1} =
2\sqrt[4]{x^{2} - 1}\).
Hướng dẫn giải
Điều kiện :\(x \geq 1\)
PT (1) \(\Leftrightarrow 3\left(
\sqrt[4]{\frac{x - 1}{x + 1}} \right)^{2} + m = 2\sqrt[4]{\frac{x - 1}{x
+ 1}}\) (2)
Đặt \(t = \sqrt[4]{\frac{x - 1}{x +
1}}\) do \(0 \leq \sqrt[4]{\frac{x -
1}{x + 1}} = \sqrt[4]{1 - \frac{2}{x + 1}} < 1 \Rightarrow 0 \leq t
< 1\)
Phương trình (2) trở thành : \(3t^{2} + m =
2t \Leftrightarrow m = - 3t^{2} + 2t\) (3)
Xét hàm số \(f(t) = - 3t^{2} + 2t\), \(t \in \lbrack 0;1)\)
Ta có : \(f'(t) = - 6t + 2\ \ \ ;\
f'(t) = 0 \Leftrightarrow t = \frac{1}{3}\)
Bảng biến thiên :
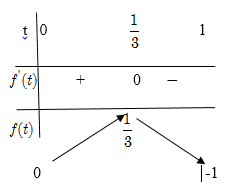
Phương trình (1) có nghiệm \(x \in \lbrack
1; + \infty) \Leftrightarrow\) phương trình (3) có nghiệm \(t \in \lbrack 0;1)\)
\(\Leftrightarrow - 1 < m \leq
\frac{1}{3}\).
B. Bài tập tự rèn luyện tìm m để phương trình có nghiệm – Có đáp án
Bài 1: Cho phương trình
\(x^{2} - 2x + m.(x - 4).\sqrt{\frac{x +
2}{4 - x}} + 2\sqrt{8 + 2x - x^{2}} - 14 - m = 0\).
Tìm m để phương trình có nghiệm thực.
Bài 2. Cho phương trình: \(\sqrt{21 + 4x -
x^{2}} - \frac{3}{4}x + 3 = m\left( \sqrt{x + 3} + 2\sqrt{7 - x}
\right)\), với m là tham số. Tìm tham số m để phương trình có nghiệm thực.
Bài 3: Tìm m để phương trình sau có nghiệm \(8x^{2} + 4x + 13 = m^{2}(2x + 1)\sqrt{x^{2} +
3}\).
Bài 4. Cho phương trình: \(\sqrt[5]{x^{2} -
34x + a} - \sqrt[4]{(x - 1)(x - 33)} = 1\).
a. Giải phương trình khi \(a =
64.\)
b. Tìm \(a\) để phương trình có nghiệm.
Bài 5. Giải và biện luận phương trình theo tham số m:
\((\lg \cos x)^{2} - m\log \cos^{2}x - m^{2} + 2= 0.\)
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
---------------------------------------------------------------
Dạng toán tìm m để phương trình có nghiệm lớp 12 bằng cách ứng dụng tính đơn điệu của hàm số không chỉ rèn luyện kỹ năng phân tích hàm số mà còn giúp bạn tư duy logic và lập luận chặt chẽ hơn. Để giải tốt dạng bài này, học sinh cần nắm vững định nghĩa đồng biến – nghịch biến, kỹ năng khảo sát hàm và đặc biệt là phương pháp biến đổi phương trình chứa tham số. Hãy luyện tập thường xuyên để tự tin chinh phục các bài toán khó trong đề thi THPT. Chúc bạn học tốt và đạt điểm cao môn Toán 12!
