Trong không gian với hệ toạ độ , gọi
là mặt phẳng song song với mặt phẳng
và cách điểm
một khoảng
. Phương trình của mặt phẳng
là:
Vì
Giả thiết có
Vậy ,
Trong chương trình Toán lớp 12, chuyên đề phương trình mặt phẳng đóng vai trò quan trọng trong phần hình học không gian. Không chỉ yêu cầu học sinh nắm vững lý thuyết, chuyên đề này còn đòi hỏi khả năng vận dụng linh hoạt vào các dạng bài thực tế và thi cử. Bài viết dưới đây cung cấp hệ thống bài tập phương trình mặt phẳng ở mức độ Thông hiểu và Vận dụng, kèm lời giải chi tiết, rõ ràng, giúp học sinh từng bước củng cố kiến thức và nâng cao tư duy giải toán. Đây là tài liệu hữu ích cho quá trình ôn thi học kỳ và kỳ thi THPT Quốc gia.
Trong không gian với hệ toạ độ , gọi
là mặt phẳng song song với mặt phẳng
và cách điểm
một khoảng
. Phương trình của mặt phẳng
là:
Vì
Giả thiết có
Vậy ,
Trong không gian với hệ toạ độ , mặt phẳng
đi qua điểm
và cắt các tia
các đoạn bằng nhau có phương trình là:
Gọi là giao điểm của mặt phẳng
và các tia
.
Phương trình mặt phẳng qua A, B, C là:
.
Mặt phẳng qua điểm
Ta có
Trong không gian với hệ toạ độ , cho
,
,
,
và mặt phẳng
. Xác định b và c biết mặt phẳng
vuông góc với mặt phẳng
và khoảng cách từ
đến
bằng
.
Phương trình mặt phẳng có dạng
Theo giả thiết:
Trong không gian với hệ trục tọa độ , cho hai mặt phẳng
,
. Giá trị số thực
để hai mặt phẳng
vuông góc
Để 2 mặt phẳng vuông góc
.
Vậy .
Trong không gian với hệ trục tọa độ , cho điểm
Mặt phẳng
qua
cắt các tia
lần lượt tại
sao cho thể tích khối tứ diện
nhỏ nhất có phương trình là:
+) Mặt phẳng cắt các tia
lần lượt tại
nên
(
).
Phương trình mặt phẳng .
+) Mặt phẳng qua
nên
.
Ta có
+) Thể tích khối tứ diện bằng
.
Thể tích khối tứ diện nhỏ nhất khi
suy ra
.
Phương trình mặt phẳng hay
.
Trong không gian với hệ toạ độ ,cho
,
. Lập phương trình mặt phẳng
chứa giao tuyến của
và cắt các trục tọa độ tại các điểm
sao cho hình chóp
là hình chóp đều.
Chọn thuộc giao tuyến của
Gọi lần lượt là giao điểm của
với các trục
chứa
Hình chóp là hình chóp đều
Vây phương trình .
Trong không gian với hệ trục tọa độ , cho điểm
. Viết phương trình mặt phẳng cắt các trục
lần lượt tại
sao cho
là trọng tâm tứ diện
?
+) Do lần lượt thuộc các trục
nên
.
+) Do là trọng tâm tứ diện
nên
suy ra .
+) Vậy phương trình đoạn chắn của mặt phẳng là:
.
Trong không gian với hệ trục tọa độ . Cho hai mặt phẳng
,
. Khoảng cách giữa hai mặt phẳng
là bao nhiêu?
Lấy thuộc mặt phẳng
.
Ta có .
Vậy .
Trong không gian với hệ trục tọa độ , cho 4 mặt phẳng
,
,
,
. Có bao nhiêu cặp mặt phẳng song song với nhau.
Hai mặt phẳng song song khi
Xét và
:
Xét và
:
Xét và
:
Xét và
:
Xét và
:
.
Vậy có 3 cặp mặt phẳng song song.
Trong không gian với hệ trục toạ độ ,cho
điểm
,
,
và mặt phẳng
. Lập phương trình mặt phẳng
đi qua
, vuông góc với mặt phẳng
cắt đường thẳng
tại
sao cho
biết tọa độ điểm
là số nguyên
Do thẳng hàng và
Vì tọa độ điểm là số nguyên nên
Lúc đó mặt phẳng đi qua
và vuông góc với mặt phẳng
.
Trong không gian với hệ trục tọa độ , cho hai mặt phẳng
,
. Với giá trị thực của
bằng bao nhiêu để
song song
Để song song
.
Vậy .
Trong không gian với hệ trục tọa độ , cho tứ diện
có các đỉnh
,
,
và
. Phương trình mặt phẳng
đi qua
đồng thời cách đều
Trường hợp 1:
Trường hợp 2: đi qua trung điểm
của
.
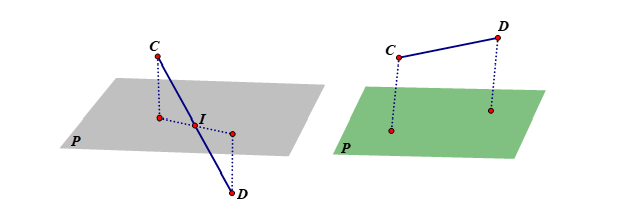
Trong không gian với hệ trục toạ độ , cho hai mặt phẳng
,
. Lập phương trình mặt phẳng
đi qua
và chứa giao tuyến của hai mặt phẳng
?
Gọi là các điểm thuộc giao tuyến của hai mặt phẳng
.
thỏa hệ phương trình :
Cho .
Cho .
Lúc đó mặt phẳng chứa 3 điểm
.
Trong không gian với hệ toạ độ , tam giác
có
,
,
. Điểm
là trọng tâm của tam giác
. Khoảng cách từ
đến mặt phẳng
bằng bao nhiêu?
Do là trọng tâm tam giác
Gọi là một vtpt của mặt phẳng
Phương trình mặt phẳng:
Trong không gian với hệ toạ độ ,cho hai đường thẳng
lần lượt có phương trình
,
. Phương trình mặt phẳng
cách đều hai đường thẳng
là:
Ta có đi qua
và có
,
đi qua
và có
;
nên
chéo nhau.
Do cách đều
nên
song song với
có dạng
Theo giả thiết thì
Trong không gian với hệ toạ độ , cho hình cầu
. Phương trình mặt phẳng
chứa
cắt hình cầu
theo thiết diện là đường tròn có chu vi bằng
Phương trình mặt phẳng
Ta có : .
Mà có tâm
Do
Chọn
Trong không gian với hệ toạ độ ,
là mặt phẳng đi qua điểm
và vuông góc với hai mặt phẳng
và
. Phương trình mặt phẳng
là:
Mặt phẳng (P) có một VTPT là
Mặt phẳng (Q) có một VTPT là
Mặt phẳng vuông góc với
mặt phẳng
,
nên có một VTPT là
.
Phương trình mặt phẳng là:
Trong không gian với hệ toạ độ , cho ba điểm
. Phương trình mặt phẳng
đi qua
và cách
một khoảng lớn nhất?
Hình vẽ minh họa
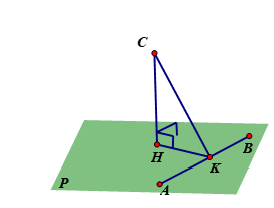
Gọi lần lượt là hình chiếu
của lên mp
và doạn thẳng
Ta có : lớn nhất khi
. Khi đó mặt phẳng
đi qua
và vuông với mặt phẳng
Ta có
Trong không gian với hệ trục tọa độ , có bao nhiêu mặt phẳng song song với mặt phẳng
và tiếp xúc với mặt cầu
?
+) Mặt phẳng song song với mặt phẳng
có dạng:
.
+) Do mặt phẳng tiếp xúc với mặt cầu
nên
với
là tâm cầu,
là bán kính mặt cầu.
Tìm được hoặc
(loại) Vậy có 1 mặt phẳng thỏa mãn.
Trong không gian với hệ toạ độ , viết phương trình mặt phẳng
đi qua hai điểm
,
đồng thời cắt các tia
lần lượt tại hai điểm
(không trùng với gốc tọa độ
) sao cho
Gọi lần lượt là giao điểm của
với các tia
Do .
Đặt
Gọi là môt vectơ pháp tuyến của mặt phẳng
Phương trình măt phẳng .
Trong không gian với hệ trục toạ độ , cho tứ diện
có điểm
,
. Trên các cạnh
lần lượt lấy các điểm
thỏa:
. Viết phương trình mặt phẳng
biết tứ diện
có thể tích nhỏ nhất?
Áp dụng bất đẳng thức ta có:
Để nhỏ nhất khi và chỉ khi
Lúc đó mặt phẳng song song với mặt phẳng
và đi qua
.
Trong không gian với hệ trục toạ độ , cho mặt cầu
, điểm
. Phương trình mặt phẳng
đi qua
và cắt mặt cầu
theo thiết diện là hình tròn
có diện tích nhỏ nhất ?
Mặt cầu có tâm
.
Ta có nên điểm
nằm trong mặt cầu.
Ta có :
Diện tích hình tròn nhỏ nhất
nhỏ nhất
lớn nhất.
Do Khi đó mặt phẳng
đi qua
và nhận
làm vtpt
Trong không gian với hệ toạ độ , gọi
là mặt phẳng qua
và cắt các trục
lần lượt tại các điểm
(khác gốc
) sao cho
là trọng tâm của tam giác
. Khi đó mặt phẳng
có phương trình:
Phương pháp tự luận
Gọi A(a; 0; 0), B(0; b; 0), C(0;0;c) là giao điểm của mặt phẳng các trục Ox, Oy, Oz
Phương trình mặt phẳng :
.
Ta có là trọng tâm tam giác
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng đi qua điểm
và cắt các trục Ox, Oy, Oz lần lượt tại
,
,
( khác gốc toạ độ
) sao cho
là trực tâm tam giác
. Mặt phẳng
có phương trình là:
Hình vẽ minh họa
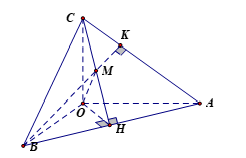
Cách 1: Gọi là hình chiếu vuông góc của
trên
,
là hình chiếu vuông góc
trên
.
là trực tâm của tam giác
khi và chỉ khi
Ta có : (1)
Chứng minh tương tự, ta có: (2).
Từ (1) và (2), ta có:
Ta có: .
Mặt phẳng đi qua điểm
và có một VTPT là
nên có phương trình là:
.
Cách 2:
+) Do lần lượt thuộc các trục
nên
(
).
Phương trình đoạn chắn của mặt phẳng là:
.
+) Do là trực tâm tam giác
nên
.
Giải hệ điều kiện trên ta được
Vậy phương trình mặt phẳng: .
Trong không gian với hệ toạ độ , cho điểm
. Viết phương trình mặt phẳng
cắt các trục
lần lượt tại
(không trùng với gốc tọa độ
) sao cho
là tâm đường tròn ngoại tiếp tam giác
?
Gọi lần lượt là giao điểm của
với các trục
Ta có:
Trong không gian với hệ trục tọa độ , cho mặt phẳng
. Gọi mặt phẳng
là mặt phẳng đối xứng của mặt phẳng
qua mặt phẳng
. Khi đó phương trình mặt phẳng
là?
Gọi là điểm bất kỳ thuộc mặt phẳng
.
Điểm là điểm đối xứng của
qua trục tung
là mặt phẳng đi qua
và là mặt phẳng đối xứng của
.
Vậy .
Trong không gian với hệ toạ độ , cho hình cầu
. Phương trình mặt phẳng
chứa trục
và tiếp xúc với
Mặt phẳng chứa trục
có dạng:
Ta có:
.
Chọn
Trong không gian với hệ trục tọa độ , cho điểm
Gọi
là mặt phẳng chứa trục
và cách
một khoảng lớn nhất. Phương trình của
là:
Hình vẽ minh họa
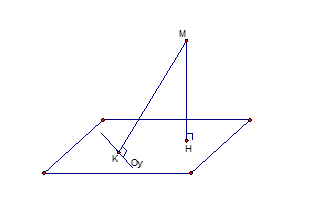
+) Gọi lần lượt là hình chiếu vuông góc của
trên mặt phẳng
và trục
.
Ta có :
Vậy khoảng cách từ đến mặt phẳng
lớn nhất khi mặt phẳng
qua
và vuông góc với
.
Phương trình mặt phẳng:
Trong không gian với hệ trục tọa độ , cho hai mặt phẳng có phương trình
và mặt cầu
. Mặt phẳng
vuông với mặt phẳng
đồng thời tiếp xúc với mặt cầu
.
Mặt cầu có tâm
và bán kính
Gọi là một vectơ pháp tuyến của mặt phẳng
Ta có :
Lúc đó mặt phẳng có dạng :
.
Do mặt phẳng tiếp xúc với mặt cầu
Vậy phương trình mặt phẳng :
hoặc
.
Trong không gian với hệ trục tọa độ , gọi
là mặt phẳng song song với mặt phẳng
và cắt mặt cầu
theo đường tròn có chu vi lớn nhất. Phương trình của
là:
Mặt phẳng cắt mặt cầu
theo đường tròn có chu vi lớn nhất nên mặt phẳng
đi qua tâm
.
Phương trình mặt phẳng song song với mặt phẳng
có dạng :
Do đi qua tâm
có phương trình dạng:
.
Trong không gian với hệ trục tọa độ , cho mặt phẳng
, 2 điểm
. Viết phương trình mặt phẳng
vuông với mặt phẳng
, song song với đường thẳng
, đồng thời cắt mặt cầu
theo đường tròn có bán kính bằng
?
Mặt cầu có tâm
và bán kính
Gọi là một vectơ pháp tuyến của mặt phẳng
Ta có :
Lúc đó mặt phẳng có dạng:
Gọi là hình chiếu của
lên mặt phẳng
Ta có :
hoặc
Vậy phương trình mặt phẳng :
hoặc
Trong không gian với hệ trục tọa độ , cho mặt phẳng
. Gọi mặt phẳng
là mặt phẳng đối xứng của mặt phẳng
qua trục tung. Khi đó phương trình mặt phẳng
là?
Gọi là điểm bất kỳ thuộc mặt phẳng
.
Điểm là điểm đối xứng của
qua trục tung
là mặt phẳng đi qua
và là mặt phẳng đối xứng của
Vậy .
Trong không gian với hệ trục tọa độ , gọi
là mặt phẳng chứa trục
và tạo với mặt phẳng
góc
. Phương trình mặt phẳng
là:
+) Mặt phẳng chứa trục
nên có dạng:
.
+) Mặt phẳng tạo với mặt phẳng
góc
nên
.
Phương trình mặt phẳng là:
Trong không gian với hệ toạ độ ,tọa độ điểm
nằm trên trục
và cách đều hai mặt phẳng:
và
là:
Ta có
Giả thiết có
Vậy
Trong không gian với hệ trục toạ độ ,cho 2 đường thẳng
. Viết phương trình mặt phẳng
vuông góc với
,cắt
tại
và cắt
tại
(có tọa nguyên) sao cho
.
Do mặt phẳng vuông góc với
.
Mặt phẳng cắt
tại
, cắt
tại
.
Vậy mặt phẳng .
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
