Các bài toán tối ưu kinh tế trong thực tế - Giải chuẩn từng bước
Bài toán tối ưu lợi nhuận chi phí - Toán 12
Trong đời sống và hoạt động sản xuất – kinh doanh, việc đưa ra quyết định sao cho lợi nhuận đạt mức cao nhất hoặc chi phí được giảm thiểu luôn là bài toán then chốt. Dưới góc nhìn Toán học, những vấn đề này được mô hình hóa thành các bài toán tối ưu kinh tế trong thực tế, nơi học sinh và người học vận dụng kiến thức đạo hàm để phân tích và lựa chọn phương án hiệu quả.
A. Bài tập minh họa tối ưu kinh tế
Ví dụ 1. Một cửa hàng bán lẻ bán 2500 cái tivi mỗi năm. Chi phí gửi trong kho là 10 USD một cái một năm. Để đặt hàng nhà sản xuất thì mỗi lần chi phí cố định là 20 USD, cộng thêm 9 USD mỗi chiếc. Biết rằng số lượng tivi trung bình gửi trong kho bằng một nửa số tivi của mỗi lần đặt hàng. Như vậy cửa hàng nên đặt hàng nhà sản xuất bao nhiêu lần mỗi năm và mỗi lần đặt bao nhiêu cái để chi phí hàng tồn kho là thấp nhất ?
A. 20 lần mỗi năm và 90 cái mỗi lần. B. 25 lần mỗi năm và 110 cái mỗi lần.
C. 25 lần mỗi năm và 120 cái mỗi lần. D. 25 lần mỗi năm và 100 cái mỗi lần.
Hướng dẫn giải
Chọn D
Gọi 
\(x\) là số tivi mỗi lần đặt hàng thì \(x \in \lbrack 1;2500\rbrack\)
Khi đó, số lượng tivi trung bình gửi trong kho sẽ là \(\frac{x}{2}\).
Do đó, chi phí gửi hàng trong khi mỗi năm sẽ là \(10.\frac{x}{2} = 5x\).
Số lần đặt hàng mỗi năm sẽ là \(\frac{2500}{x}\).
Do đó chi phí đặt hàng mỗi năm sẽ là \((20
+ 9x).\frac{2500}{x} = \frac{50000}{x} + 22500\).
Suy ra, chi phí hàng tồn kho là \(C(x) = 5x
+ \frac{50000}{x} + 22500\).
Bài toán trở thành tìm giá trị nhỏ nhất của \(C(x)\) với \(x \in
\lbrack 1;2500\rbrack\).
Ta có:
\(C^{'(x)} = 5 -
\frac{50000}{x^{2}},C^{'(x)} = 0\)\(\Leftrightarrow x^{2} = 100^{2}
\Leftrightarrow \left\lbrack \begin{matrix}
x = 100(tm) \\
x = - 100(ktm)
\end{matrix} \right.\)
Do \(C''(x) = \frac{100000}{x^{3}}
> 0,\forall x \in \lbrack 1;2500\rbrack\) nên \(\min_{x \in \lbrack 1;2500\rbrack}C(x) = C(100) =
23500\)
Khi đó số lần đặt hàng mỗi năm sẽ là \(\frac{2500}{100} = 25\) lần.
Vậy để chi phí hàng tồn kho là nhỏ nhất thì cửa hàng cần đặt hàng 25 lần mỗi năm và 100 cái mỗi lần.
Ví dụ 2. Công ty xe khách Gin-Bơ dự định tăng giá vé trên mỗi hành khách. Hiện tại giá vé là \(50.000\)VNĐ một khách và có \(10.000\) khách trong một tháng. Nhưng nếu tăng giá vé thêm \(1.000\)VNĐ một hành khách thì số khách sẽ giảm đi \(50\)người mỗi tháng. Hỏi công ty sẽ tăng giá vé là bao nhiêu đối với một khách để có lợi nhuận lớn nhất?
A. \(50.000\) VNĐ. B. \(15.000\) VNĐ. C. \(35.000\) VNĐ. D. \(75.000\) VNĐ.
Hướng dẫn giải
Chọn D
Gọi \(x\)(nghìn VNĐ) là số tiền công ty sẽ tăng thêm đối với một khách.
Khi đó số khách sẽ giảm đi là \(50x\)khách nên còn \(10.000 - 50x\) khách.
Khi đó, \(10.000 - 50x > 0
\Leftrightarrow x < 200\).
Khi đó số tiền thu được sau khi tăng giá vé là \(f(x) = (50 + x)(10.000 - 50x)\).
Ta có \(f(x) = 50(50 + x)(200 - x) \leq
50\left( \frac{50 + x + 200 - x}{2} \right)^{2} = 781250\) (nghìn VNĐ).
Vậy số tiền thu được tăng thêm lớn nhất là \(781250 - 50.10000 = 281250\) nghìn VNĐ khi \(50 + x = 200 - x \Leftrightarrow x =
75\) nghìn VNĐ.
Ví dụ 3. Một công ty bất động sản có \(50\)căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá \(2.000.000\) đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê, mỗi căn hộ thêm \(50.000\)đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
A. \(115.250.000\). B. \(101.250.000\). C. \(100.000.000\). D. \(100.250.000\).
Hướng dẫn giải
Chọn B
Ở tháng thu nhập của công ty cao nhất, gọi số căn hộ bị bỏ trống là \(x\) thì số tiền thuê mỗi phòng là \(2.000.000 + 50.000x\), khi đó số tiền thu được là:
\(f(x) = (2.000.000 + 50.000x)(50 - x)\)\(= -50.000x^{2} + 500.000x + 100.000.000\).
Ta cần tìm \(x \in (0;\ 50)\)để \(f(x)\)lớn nhất.
Ta có \(f'(x) = - 100.000x +
500.000\), \(f'(x) = 0
\Leftrightarrow x = 5\)
Bảng biến thiên:
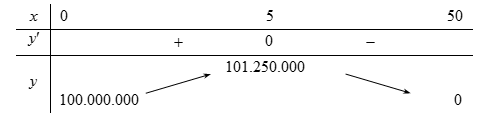
Vậy mỗi tháng lợi nhuận cao nhất thu được của công ty là \(101.250.000\).
B. Bài tập vận dụng có hướng dẫn giải chi tiết
Bài tập 1. Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là \(50.000\) đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng \(40\) quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả \(5000\) đồng thì số bưởi bán được tăng thêm là \(50\)quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là \(30.000\) đồng.
A. \(44.000\) đồng. B. \(43.000\) đồng. C. \(42.000\) đồng. D. \(41.000\) đồng.
Bài tập 2. Một xưởng in có \(8\)máy in, mỗi máy in được \(3600\)bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là \(50\)nghìn đồng. Chi phí cho \(n\)máy chạy trong một giờ là \(10(6n + 10)\)nghìn đồng. Hỏi nếu in \(50000\)tờ quảng cáo thì phải sử dụng bao nhiêu máy in để được lãi nhiều nhất?
A. \(4\) máy. B. \(6\) máy. C. \(5\) máy. D. \(7\) máy.
Bài tập 3. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng \(P(n) = 480 -
20n(gam)\). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
A. \(10\) B. \(12\) C. \(16\) D. \(24\)
Bài tập 4. Một chuyến xe bus có sức chứa tối đa là \(60\) hành khách. Nếu một chuyến xe chở \(x\) hành khách thi giá cho mỗi hành khách là \(\left( 3 - \frac{x}{40}
\right)^{2}\$\). Chọn câu đúng:
A. Xe thu được lợi nhuận cao nhất khi có 60 hành khách.
B. Xe thu được lợi nhuận cao nhất bằng \(135\$\).
C. Xe thu được lợi nhuận cao nhất bằng \(160\$\).
D. Không có đáp án đúng.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
------------------------------------------------
Thông qua việc rèn luyện các bài toán tối ưu kinh tế, người học không chỉ nắm chắc phương pháp tìm lợi nhuận lớn nhất, chi phí nhỏ nhất mà còn phát triển tư duy phân tích và ra quyết định hợp lý. Việc giải bài theo từng bước rõ ràng giúp hạn chế sai sót, đồng thời tạo nền tảng vững chắc để xử lý những dạng toán ứng dụng nâng cao.
Hy vọng nội dung bài viết sẽ trở thành tài liệu tham khảo hữu ích, hỗ trợ bạn học tốt Toán ứng dụng và vận dụng hiệu quả vào các bài toán thực tế trong các đề thi THPT Quốc gia.
