Bài tập tìm m để hàm số đồng biến trên khoảng, đoạn cho trước
Bài tập Toán 12: Tìm m để hàm số đồng biến (Có đáp án)
Dạng toán tìm tham số m để hàm số đồng biến trên một khoảng hoặc đoạn xác định là nội dung quan trọng trong chương Ứng dụng đạo hàm Toán 12, thường xuyên xuất hiện trong đề thi tốt nghiệp và các bài kiểm tra đánh giá năng lực. Bài viết này tổng hợp hệ thống bài tập tiêu biểu, có phân tích điều kiện đạo hàm và đáp án chi tiết, giúp học sinh hiểu rõ bản chất tính đơn điệu của hàm số chứa tham số, từ đó rèn luyện kỹ năng làm bài nhanh và chính xác.
A. Cách tìm m để hàm số đồng biến trên khoảng cho trước
Cách 1. Cho hàm số 
\(y = f(x)\) có đạo hàm trên khoảng \((a,b)\). Hàm số \(y = f(x)\) đồng biến trên khoảng \((a,b)\) khi và chỉ khi \(f'(x) \geq 0\) với mọi giá trị x thuộc khoảng \((a,b)\). Dấu bằng xảy ra tại hữu hạn điểm.
Chú ý:
-
Hàm số
\(f(x) = \frac{ax + b}{cx +
d},(ad - bc \neq 0,c \neq 0)\) đồng biến trên từng khoảng xác định khi và chỉ khi \(ad - bc >
0\) -
Hàm số
\(g(x) = \frac{ax + b}{cx +
d}(ad - bc \neq 0,c \neq 0)\) đồng biến trên khoảng \((p,q)\) khi và chỉ khi \(\left\{ \begin{matrix}
cx + d \neq 0,\forall x \in (p,q) \\
ad - bc > 0
\end{matrix} \right.\)
Cách 2. Cô lập tham số m
Cho hàm số \(y = f(x)\)có đạo hàm trên khoảng \((p;q)\)
-
Bước 1: Tìm y’
-
Bước 2: Cô lập m ta sẽ thu được phương trình ví dụ
\(m \geq f(x)\) -
Bước 3: Xét dấu với hàm
\(f(x)\) theo bảng quy tắc sau:
\(m \geq f(x),\forall x \in (p,q)
\Leftrightarrow m \geq \max_{(p,q)}f(x)\)
\(m > f(x),\forall x \in (p,q)
\Leftrightarrow m > \max_{(p,q)}f(x)\)
\(m \leq f(x),\forall x \in (p,q)
\Leftrightarrow m \leq \min_{(p,q)}f(x)\)
\(m < f(x),\forall x \in (p,q)
\Leftrightarrow m < \min_{(p,q)}f(x)\)
B. Bài tập minh họa tìm m để hàm số đồng biến trên khoảng, đoạn
Ví dụ 1. Hàm số \(y = x^{3} - 6x^{2} + mx +
1\) đồng biến trên miền \((0; +
\infty)\) khi giá trị của \(m\) thỏa mãn:
A. \(m \geq 12\). B. \(m \leq 0\). C. \(m \leq 12\). D. \(m > 12\).
Hướng dẫn giải
Chọn A
Tập xác định: \(D\mathbb{=
R}.\).
Ta có: \(y' = 3x^{2} - 12x +
m.\)
Để hàm số đồng biến trên \((0; +
\infty)\) khi và chỉ khi:
\(y' \geq 0,\forall x \in (0;\ \ +\infty)\)
\(\Leftrightarrow 3x^{2} - 12x + m \geq 0,\forall x \in (0;\ \ +\infty)\)
\(\Leftrightarrow m \geq - 3x^{2} + 12x,\forall x \in (0; +\infty)\).
Xét hàm số:
\(g(x) = - 3x^{2} + 12x,\forall
x \in (0;\ \ + \infty)\).
Ta có: \(g^{'(x)} = - 6x + 12;\ \
g^{'(x)} = 0 \Leftrightarrow - 6x + 12 = 0\)
\(\Leftrightarrow x = 2 \Rightarrow g(2) =
12.\).
Bảng biến thiên:
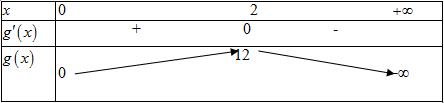
Vậy ta có: \(m \geq g(x) \Leftrightarrow m
\geq \max_{(0; + \infty)}g(x) \Leftrightarrow m \geq 12\).
Ví dụ 2. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = x^{3} - 3(2m + 1)x^{2} + (12m + 5)x +
2\) đồng biến trên khoảng \((2;\ +
\infty)\). Số phần tử của \(S\) bằng
A. \(3\) B. \(0\) C. \(1\) D. \(2\)
Hướng dẫn giải
Chọn B
Tập xác định \(D\mathbb{= R}\).
\(y' = 3x^{2} - 6(2m + 1)x + 12m +
5\).
Hàm số đồng biến trong khoảng \((2;\ +
\infty)\) khi \(y' \geq 0\), \(\forall x \in (2;\ + \infty)\)
\(\Leftrightarrow 3x^{2} - 6(2m + 1)x + 12m + 5 \geq
0\), \(\forall x \in (2; +
\infty)\).
\(3x^{2} - 6(2m + 1)x + 12m + 5 \geq
0\)
\(\Leftrightarrow m \leq
\frac{3x^{2} - 6x + 5}{12(x - 1)}\)
Xét hàm số \(g(x) = \frac{3x^{2} - 6x +
5}{12(x - 1)}\)với \(x \in (2;\ +
\infty)\).
\(g'(x) = \frac{3x^{2} - 6x + 1}{12(x -
1)^{2}} > 0\) với \(\forall x \in
(2;\ + \infty)\) \(\Rightarrow\) Hàm số \(g(x)\) đồng biến trên khoảng \((2;\ + \infty)\).
Do đó \(m \leq g(x)\),\(\forall x \in (2;\ + \infty)\) \(\Rightarrow m \leq g(2)\) \(\Leftrightarrow m \leq \frac{5}{12}\).
Vậy không có giá trị nguyên dương nào của \(m\) thỏa mãn bài toán.
Ví dụ 3. Cho hàm số \(y = \frac{1}{3}x^{3}
- \frac{(m + 2)}{2}x^{2} + 2mx + 1\) với \(m\) là tham số thực. Tập hợp các giá trị của \(m\) để hàm số đồng biến trên khoảng \((0\ ;\ 1)\) là
A. \(( - \infty\ ;\ 1\rbrack\). B. \(\lbrack 1\ ;\ + \infty)\). C. \(( - \infty\ ;\ 1)\). D. \((1\ ;\ + \infty)\).
Hướng dẫn giải
Chọn B
Cách 1:
Ta có \(y = \frac{1}{3}x^{3} - \frac{(m +2)}{2}x^{2} + 2mx + 1\)\(\Rightarrow y' = x^{2} - (m + 2)x +2m\).
\(y' = 0 \Leftrightarrow \left\lbrack
\begin{matrix}
x = m \\
x = 2
\end{matrix} \right.\).
Để hàm số đồng biến trên khoảng \((0\ ;\
1)\) thì \(\left\lbrack \begin{matrix}
0 < 1 \leq m \leq 2 \\
0 < 1 \leq 2 \leq m
\end{matrix} \right.\ \Rightarrow m \geq 1\).
Do đó \(m \in \lbrack 1\ ;\ +
\infty)\).
Cách 2:
Hàm số đã cho đồng biến trên khoảng \((0\
;\ 1)\)
\(\Leftrightarrow y' = x^{2} - (m + 2)x
+ 2m \geq 0\) \(\forall x \in (0\ ;\
1)\)
\(\Leftrightarrow (x - 2)(x - m) \geq
0\) \(\forall x \in (0\ ;\ 1)
\Leftrightarrow x \leq m\) \(\forall x
\in (0\ ;\ 1)\).
Vậy \(m \geq 1\).
C. Bài tập vận dụng có đáp án chi tiết
Bài tập 1. Tìm tất cả các giá trị thực của tham số \(m\) sao cho hàm số \(y = x^{4} - 2(m - 1)x^{2} + m - 2\) đồng biến trên khoảng \((1;3)\).
A. \(m \in ( - \infty; - 5)\). B. \(m \in (2; + \infty)\).
C. \(m \in \lbrack - 5;2)\). D. \(m \in ( - \infty;2\rbrack\).
Bài tập 2. Bất phương trình \(\frac{x -
1}{x + 1} \geq m\) có nghiệm thuộc đoạn \(\lbrack 1;2\rbrack\) khi và chỉ khi
A. \(m \leq \frac{1}{3}\). B. \(m \leq 0\). C. \(m \geq 0\). D. \(m \geq \frac{1}{3}\).
Bài tập 3. Tập tất cả các giá trị thực của tham số \(m\) để hàm số \(y
= mx - \frac{1}{x^{3}} + 2x^{3}\) đồng biến trên khoảng \((0 ; + \infty)\) là
A. \(\lbrack - 9\ ;\ + \infty)\). B. \(( - \infty\ ;\ - 9)\). C. \(( - 9\ ;\ + \infty)\). D. \(( - \infty\ ;\ - 9\rbrack\).
Bài tập 4. Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y= \sin^{3}x - 3\cos^{2}x - m\sin x - 1\) đồng biến trên đoạn \(\left\lbrack 0;\frac{\pi}{2}
\right\rbrack\).
A. \(m \leq 0\). B. \(m \leq - 3\). C. \(m > 0\). D. \(m > - 3\).
Bài tập 5. Tìm tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y
= x^{3} - 6x^{2} + mx + 1\) đồng biến trên khoảng \((0\ ; + \infty)\).
A. \(\lbrack 3\ ; + \infty)\). B. \(\lbrack 48\ ; + \infty)\). C. \(\lbrack 36\ ; + \infty)\). D. \(\lbrack 12\ ; + \infty)\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
-----------------------------------
Thông qua chuyên đề này, bạn đã được củng cố phương pháp xác định m để hàm số đồng biến trên khoảng hoặc đoạn cho trước một cách logic và hiệu quả. Việc luyện tập thường xuyên các dạng bài có đáp án sẽ giúp bạn tránh sai sót khi xét dấu đạo hàm và nâng cao khả năng xử lý các câu hỏi vận dụng trong đề thi Toán 12. Đừng quên kết hợp thêm các chuyên đề nghịch biến và cực trị để hoàn thiện kiến thức về khảo sát hàm số.
