Bộ bài tập tìm m để bất phương trình nghiệm đúng với mọi x (Có lời giải)
Điều kiện để bất phương trình đúng với mọi x
Trong quá trình ôn thi THPT Quốc gia môn Toán, dạng toán tìm tham số m để bất phương trình nghiệm đúng với mọi x luôn được đánh giá là khó và dễ gây nhầm lẫn. Bài viết này tổng hợp bộ bài tập chọn lọc, phân loại theo từng phương pháp giải quen thuộc, kèm lời giải chi tiết và chặt chẽ.
A. Cách tìm m để bpt nghiệm đúng với mọi x
Tìm giá trị của tham số 
\(m\) để bất phương trình \(\left| \begin{matrix}
F(x;m) > 0;F(x;m) \geq 0 \\
F(x;m) < 0;F(x;m) \leq 0
\end{matrix} \right.\) có nghiệm trên \(D\).
Phương pháp:
- Bước 1: Cô lập tham số \(m\) và đưa về dạng \(A(m) > f(x)\) hoặc \(A(m) \geq f(x)\) hoặc \(A(m) < f(x)\) hoặc \(A(m) \leq f(x)\).
- Bước 2: Khảo sát sự biến thiên của hàm số \(f(x)\) trên \(D\)
- Bước 3: Dựa vào bảng biến thiên của hàm số xác định các giá trị của \(m\)
Chú ý: Nếu hàm số \(y = f(x)\) có giá trị lớn nhất và giá trị nhỏ nhất trên \(D\)
-
Bất phương trình
\(A(m) \geq
f(x)\) nghiệm đúng \(\forall x \in D
\Leftrightarrow A(m) \geq \max_{D}f(x)\) -
Bất phương trình
\(A(m) \leq
f(x)\) nghiệm đúng \(\forall x \in D
\Leftrightarrow A(m) \leq \min_{D}f(x)\) -
Bất phương trình
\(A(m) \geq
f(x)\) nghiệm đúng trên \(D
\Leftrightarrow A(m) \geq \min_{D}f(x)\) -
Bất phương trình
\(A(m) \leq
f(x)\) nghiệm đúng trên \(D
\Leftrightarrow A(m) \leq \max_{D}f(x)\)
B. Bài tập minh họa tìm m để bpt nghiệm đúng với moi x
Ví dụ 1. Tính tổng các giá trị nguyên của tham số \(m \in \lbrack - 50;50\rbrack\) sao cho bất phương trình \(mx^{4} - 4x + m \geq 0\) nghiệm đúng với mọi \(x\mathbb{\in
R}\).
Hướng dẫn giải
Ta có
\(mx^{4} - 4x + m \geq 0
\Leftrightarrow m\left( x^{4} + 1 \right) \geq 4x\)
\(\Leftrightarrow m \geq \frac{4x}{x^{4} +
1}\) với \(\forall x\mathbb{\in
R}\).
Do đó, \(m \geq \min_{x\mathbb{\in
R}}\frac{4x}{x^{4} + 1}\).
Xét hàm \(f(x) = \frac{4x}{x^{4} +
1}\) trên \(\mathbb{R}\).
Ta có \(f^{'(x)} = 4\frac{x^{4} + 1 -
x\left( 4x^{3} \right)}{\left( x^{4} + 1 \right)^{2}}\)
\(= 4.\frac{- 3x^{4} + 1}{\left( x^{4} + 1
\right)^{2}} = 4.\frac{\left( \sqrt{3}x^{2} + 1 \right)\left( -
\sqrt{3}x^{2} + 1 \right)}{\left( x^{4} + 1 \right)^{2}}\), đo đó \(f'(x) = 0 \Leftrightarrow x = \mp
\frac{1}{\sqrt[4]{3}}\).
Bảng biến thiên:
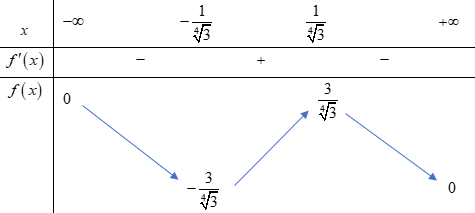
Do đó, \(m \geq - \frac{3}{\sqrt[4]{3}}
\approx - - 2,27\), vì \(m\) nguyên nên suy ra \(m \geq - 2\). Do đó, tổng bằng
\(S = ( - 2) + ( - 1) + 0 + 1 + ... + 50 =
1272\).
Ví dụ 2. Bất phương trình \(4^{x} - (m +
1)2^{x + 1} + m \geq 0\) nghiệm đúng với mọi \(x \geq 0\). Tập tất cả các giá trị của \(m\) là
A. \(( - \infty\ ;12)\). B. \(( - \infty\ ; - 1\rbrack\). C. \(( - \infty\ ;0\rbrack\). D. \(( - 1\ ;16\rbrack\).
Hướng dẫn giải
Chọn B
Ta có:
\(4^{x} - (m + 1)2^{x + 1} + m \geq 0,\ \ \
\forall x \geq 0\).
\(\Leftrightarrow \left( 2^{x} \right)^{2}
- 2(m + 1)2^{x} + m \geq 0\), \(\forall x \geq 0\) (1).
Đặt \(t = 2^{x},\ \ (t >
0)\).
(1) trở thành \(t^{2} - 2(m + 1)t + m \geq
0\), \(\forall t \geq 1\) (2).
(2)\(\Leftrightarrow m \leq \frac{t^{2} -
2t}{2t - 1}\), \(\forall t \geq
1\) (3).
Xét hàm số \(y = f(t) = \frac{t^{2} -
2t}{2t - 1}\).
Ta có hàm số \(y = f(t)\) liên tục trên \(\lbrack 1\ ;\ + \infty)\).
\(f'(t) = \frac{(2t - 2)(2t - 1) -
2\left( t^{2} - 2t \right)}{(2t - 1)^{2}} = \frac{2t^{2} - 2t + 2}{(2t -
1)^{2}} > 0\), \(\forall t \geq
1\).
Suy ra hàm số \(f(t)\) đồng biến trên \(\lbrack 1\ ;\ + \infty) \Rightarrow
f(t) \geq f(1) = - 1\), \(\forall t
\geq 1\).
Do đó (3) \(\Leftrightarrow m \leq
\min_{\lbrack 1\ ;\ + \infty)}f(t) \Leftrightarrow m \leq -
1\)
C. Bài tập vận dụng có đáp án chi tiết
Bài tập 1. Tìm số thực \(m\) lớn nhất để bất phương trình sau nghiệm đúng với mọi \(x\mathbb{\in R}:m\left( \left| \sin x \right| +
\left| \cos x \right| + 1 \right) \leq |sin2x| + \left| \sin x \right| +
\left| \cos x \right| - 2018.\)
A. \(- \frac{1}{3}.\) B. \(- 2018.\) C. \(-
\frac{2017}{2}.\) D. \(-
2017.\)
Bài tập 2. Cho bất phương trình \(8^{x} -
3.2^{2x + 1} + 9.2^{x} + m - 5 > 0\ \ \ \ (1)\). Có tất cả bao nhiêu giá trị nguyên dương của tham số \(m\) để bất phương trình \((1)\) nghiệm đúng với mọi \(x \in \lbrack 1;2\rbrack\)?
A. Vô số. B. 4. C. 5. D. 6.
Bài tập 3. Số giá trị nguyên của tham số \(m \in \lbrack - 10\ ;\ 10\rbrack\) để bất phương \(\sqrt{3 + x} + \sqrt{6 - x} -
\sqrt{18 + 3x - x^{2}} \leq m^{2} - m + 1\) nghiệm đúng \(\forall x \in \lbrack - 3\ ;\
6\rbrack\).
A. \(28\). B. \(20\). C. \(4\). D. \(19\).
Bài tập 4. Cho \(f(x)\) mà hàm số \(y = f'(x)\) có bảng biến thiên như hình vẽ bên. Tất cả các giá trị của tham số \(m\) để bất phương trình \(m + x^{2} < f(x) + \frac{1}{3}x^{3}\) nghiệm đúng với mọi \(x \in (0;3)\) là
A. \(m < f(0)\). B. \(m \leq f(0)\).
C. \(m \leq f(3)\). D. \(m < f(1) - \frac{2}{3}\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
---------------------------------------
Hy vọng bộ bài tập trong chuyên đề đã giúp bạn nắm vững cách xác định m để bất phương trình đúng với mọi giá trị x. Việc luyện tập thường xuyên các dạng bài có lời giải chi tiết sẽ giúp bạn phản xạ nhanh hơn và tự tin hơn khi bước vào phòng thi. Hãy tiếp tục ôn luyện thêm các chuyên đề tham số để hoàn thiện kỹ năng giải toán và nâng cao điểm số trong kỳ thi THPT Quốc gia.
