Bài tập Xác suất toàn phần Công thức Bayes mức độ VD - VDC

Tỉ lệ người dân đã tiêm vắc xin phòng bệnh ở một địa phương là . Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh là ; trong số những người chưa tiêm, tỉ lệ mắc bệnh là . Chọn ngẫu nhiên một người ở địa phương đó. Tính xác suất người được chọn mắc bệnh .

Có 3 hộp đựng bi giống nhau, mỗi hộp đựng 5 bi trắng và 7 bi đỏ có cùng kích thước, và trọng lượng. Lần thứ nhất lấy 1 bi từ hộp I bỏ sang hộp II, lần thứ hai lấy 1 từ hộp II bỏ sang hộp III. Cuối cùng lấy 1 bi từ hộp III ra ngoài. Tính xác suất để bi lấy ra đó là bi trắng. (làm tròn kết quả đến hàng phần trăm)

Một trạm chỉ phát hai tín hiệu và với xác suất tương ứng 0,85 và 0,15 do có nhiễu trên đường truyền nên tín hiệu bị méo và thu được như tín hiệu ; còn tín hiệu bị méo thành và thu được như. Xác suất thu được tín hiệu là

Một kho hàng có sản phẩm loại I và sản phẩm loại II, trong đó có sản phẩm loại I bị hỏng, sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách hàng chọn ngẫu nhiên 1 sản phẩm. Tính xác suất để sản phẩm đó loại I và sản phẩm đó không bị hỏng. (kết quả làm tròn đến hàng phần trăm)

Trong một đoàn du lịch đi tham quan Hội An, gồm có 10 nam và 12 nữ, hướng dẫn viên du lịch chọn ngẫu nhiên từ danh sách đoàn lần lượt 2 người. Tính xác suất để hướng dẫn viên chọn được lần 2 là người nam. (kết quả làm tròn đến hàng phần trăm)

Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai. Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.

Một hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số. Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số bằng

Bạn Tuấn hằng ngày ăn sáng bằng xôi hoặc bún. Nếu hôm nay bạn ăn sáng bằng xôi thì xác suất để hôm sau bạn ăn sáng bằng bún là . Xét một tuần mà thứ ba bạn ăn sáng bằng xôi. Biết xác suất để thứ năm tuần đó, bạn Tuấn ăn sáng bằng bún là . Hỏi nếu hôm nay bạn ăn sáng bằng bún thì xác suất để hôm sau bạn ăn sáng bằng xôi là

Trong một cửa hàng có 18 bóng đèn loại I và 2 bóng đèn loại II, các bóng đèn có hình dạng và kích thước như nhau. Một một người mua hàng lấy ngẫu nhiên lần lượt 2 bóng đèn (lấy không hoàn lại) trong cửa hàng. Biết xác suất để ít nhất 1 lần lấy được bóng đèn loại I bằng (với là các số nguyên dương và là phân số tối giản). Tính .

Một chiếc hộp có viên bi, trong đó có viên bi màu đỏ và viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Bạn Minh lấy viên bi từ hộp sau đó bạn Châu lấy viên bi thứ hai. Tính xác suất để bạn Châu lấy được viên bi màu đỏ.

Hai máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất máy II sản xuất tổng sản lượng. Tỉ lệ phế phẩm của các máy lần lượt là và Chọn ngẫu nhiên 1 sản phẩm từ kho. Tính xác suất để chọn được phế phẩm do máy I sản xuất?

Một thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo là . Biết rằng, có một loại xét nghiệm mà nếu mắc bệnh hiểm nghèo thì với xác suất xét nghiệm cho kết quả dương tính; nếu không bị bệnh hiểm nghèo thì với xác suất xét nghiệm cho kết quả âm tính. Hỏi khi một người xét nghiệm cho kết quả dương tính thì xác suất mắc bệnh hiểm nghèo của người đó là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?

Một xưởng sản xuất linh kiện điện tử có hai dây chuyền A và B. Dây chuyền A sản xuất số linh kiện, dây chuyền B sản xuất số linh kiện. Tỷ lệ phế phẩm của dây chuyền A là , của dây chuyền B là . Chọn ngẫu nhiên một linh kiện. Tính xác suất để linh kiện đó là phế phẩm.

Tại trường THPT có học sinh tham gia câu lạc bộ bơi lội, trong số học sinh đó có học sinh biết bơi ếch. Ngoài ra, có số học sinh không tham gia câu lạc bộ bơi lội cũng biết bơi ếch. Chọn ngẫu nhiên 1 học sinh của trường. Giả sử học sinh đó biết bơi ếch. Xác suất chọn được học sinh thuộc câu lạc bộ bơi lội là bao nhiêu?

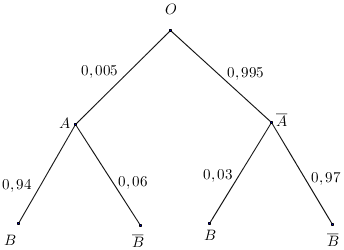
Giả sử có một loại bệnh mà tỉ lệ người mắc bệnh là . Giả sử có một loại xét nghiệm, mà ai mắc bệnh khi xét nghiệm thì có phản ứng dương tính, nhưng tỉ lệ phản ứng dương tính giả là (tức là trong số những người không bị bệnh có số người xét nghiệm lại có phản ứng dương tính). Biết khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó là . Hỏi gần số nào nhất trong các số sau?

Có hai chiếc hộp đựng bóng. Hộp I có quả bóng trắng và quả bóng xanh. Hộp II có quả bóng trắng và quả bóng xanh. Trước tiên, từ hộp I lấy ra ngẫu nhiên quả bóng rồi cho vào hộp II. Sau đó, từ hộp II lấy ra ngẫu nhiên quả bóng. Xác suất để quả bóng được lấy ra màu trắng là

Một loại linh kiện do hai nhà máy số I và số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I và II lần lượt là và . Trong một lô linh kiện để lẫn lộn sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó. Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao hơn?

Giả sử tỉ lệ người dân của tỉnh X nghiện thuốc lá là . Tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là , còn tỉ lệ này đối với người không nghiện thuốc lá là . Gặp ngẫu nhiên một người dân của tỉnh X, biết rằng người này bị bệnh phổi, tính xác suất mà người này nghiện thuốc lá?

Tại công ty Yến Sào, có hai thùng I và II chứa các hộp đựng yến sào có khối lượng và hình dạng như nhau. Thùng I có 5 hộp yến từ tự nhiên và 4 hộp yến nuôi, thùng 2 có 6 hộp yến từ tự nhiên và 8 hộp yến nuôi. Lấy ngẫu nhiên 1 hộp từ thùng I bỏ sang thùng II. Sau đó, lấy ngẫu nhiên 1 hộp từ thùng II để sử dụng. Xác suất lấy được hộp yến từ tự nhiên ở thùng II là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Một ứng dụng được sử dụng để chặn cuộc gọi rác trong điện thoại. Tuy nhiên, vì ứng dụng không tuyệt đối hoàn hảo nên một cuộc gọi rác bị chặn với xác suất và một cuộc gọi đúng (không phải là cuộc gọi rác) bị chặn với xác suất . Thống kê cho thấy tỉ lệ cuộc gọi rác là . Chọn ngẫu nhiên một cuộc gọi không bị chặn. Xác suất để đó là cuộc gọi đúng là

Một cửa hàng bán trứng gà, có hai loại trứng, trong đó có loại trứng gà Mỹ và trứng gà Nga, các trứng có kích thước như nhau. Các trứng gà Mỹ có tỉ lệ bị ung (hư) là và các trứng gà Nga có tỉ lệ bị ung là . Một khách hàng chọn mua ngấu nhiên 1 trứng gà từ cửa hàng. Tính xác suất để chọn được trứng không bị ung. (Kết quả làm tròn đến hàng phần trăm)