VnDoc.com

Tìm m để phương trình có nghiệm thuộc khoảng, đoạn

Hàm số Toán 12 ôn thi THPT Quốc gia

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập tìm m để phương trình có nghiệm trong đoạn

A. Phương pháp giải
B. Bài tập minh họa tìm m để phương trình có nghiệm thuộc khoảng đoạn
C. Bài tập tự rèn luyện có hướng dẫn chi tiết

Trong chương Hàm số Toán 12, dạng toán tìm m để phương trình có nghiệm thuộc khoảng, đoạn là nội dung then chốt giúp đánh giá khả năng vận dụng kiến thức hàm số vào bài toán tham số. Đây cũng là dạng bài xuất hiện thường xuyên trong đề thi THPT Quốc gia, đòi hỏi học sinh xác định chính xác mối liên hệ giữa nghiệm phương trình và miền giá trị của biến. Bài viết này sẽ hệ thống cách tiếp cận rõ ràng, giúp bạn xử lý dạng toán nhanh và chính xác.

A. Phương pháp giải

Biện luận số nghiệm của phương trình $f(x) = f(m)$ $(*)$

Phương pháp:

Bước 1: Cô lập tham số $m$ và đưa về dạng $f(x) = f(m)$.
Bước 2: Khảo sát sự biến thiên của hàm số $f(x)$ trên $D$.
Bước 3: Dựa vào bảng biến thiên để sác định giá trị tham số $f(m)$ sao cho đường thẳng $y = f(m)$ nằm ngang vắt đồ thị hàm số $y = f(x)$.
Bước 4: Kết luận giá trị của $f(m)$ để phương trình $f(x) = f(m)$ có nghiệm trên $D$.

Chú ý:

⏵Nếu hàm số $y = f(x)$ có giá trị lớn nhất và giá trị nhỏ nhất trên $D$ thì phương trình $f(x) = A(m) \Leftrightarrow \min_{D}f(x) \leq f(m) \leq \max_{D}f(x)$ $f(x) = A(m) \Leftrightarrow \min_{D}f(x) \leq f(m) \leq \max_{D}f(x)$

⏵Nếu bài toán yêu cầu tìm tham số để phương trình có $k$ nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên để xác định sao cho đường thẳng $y = f(m)$ nằm ngang cắt đồ thị hàm số $y = f(x)$ tại $k$ điểm phân biệt.

B. Bài tập minh họa tìm m để phương trình có nghiệm thuộc khoảng đoạn

Ví dụ 1. Tìm tất cả các giá trị của tham số $m$để phương trình $(m - 1)x^{3} + 2mx^{2} - x + 3m = 0$ $(m - 1)x^{3} + 2mx^{2} - x + 3m = 0$ có nghiệm thuộc khoảng $(0\ ;\ 1)$ $(0\ ;\ 1)$.

Hướng dẫn giải

Phương trình đã cho $\Leftrightarrow m = \frac{x^{3} + x}{x^{3} + 2x^{2} + 3}$ $\Leftrightarrow m = \frac{x^{3} + x}{x^{3} + 2x^{2} + 3}$.

Xét $f(x) = \frac{x^{3} + x}{x^{3} + 2x^{2} + 3}$ $f(x) = \frac{x^{3} + x}{x^{3} + 2x^{2} + 3}$ có $f'(x) = \frac{2x^{4} - 2x^{3} + 7x^{2} + 3}{\left( x^{3} + 2x^{2} + 3 \right)^{2}} > 0,\ \ \forall x \in (0;1)$

Nên để phương trình đã cho có nghiệm thì $f(0) < m < f(1)$ hay $0 < m < \frac{1}{3}$ $0 < m < \frac{1}{3}$.

Ví dụ 2. Tìm tất cả các giá tri của $m$ để phương trình $x^{4} + \frac{16}{x^{4}} - 4\left( x^{2} + \frac{4}{x^{2}} \right) - 12\left( x - \frac{2}{x} \right) = m$ $x^{4} + \frac{16}{x^{4}} - 4\left( x^{2} + \frac{4}{x^{2}} \right) - 12\left( x - \frac{2}{x} \right) = m$ có nghiệm $x \in \lbrack 1;\ \ 2\rbrack.$ $x \in \lbrack 1;\ \ 2\rbrack.$

A. $- 13 \leq m \leq 11.$ $- 13 \leq m \leq 11.$ B. $- 15 \leq m \leq 9.$ $- 15 \leq m \leq 9.$

C. $- 15 < m < 9.$ D. $- 16 \leq m \leq 9.$ $- 16 \leq m \leq 9.$

Hướng dẫn giải

Chọn B

Đặt $t = x - \frac{2}{x}$ $t = x - \frac{2}{x}$, $x \in \lbrack 1;\ \ 2\rbrack$ $x \in \lbrack 1;\ \ 2\rbrack$

Đạo hàm $t' = 1 + \frac{2}{x^{2}} > 0$, $\forall x \in \lbrack 1;\ \ 2\rbrack$ $\forall x \in \lbrack 1;\ \ 2\rbrack$

Do đó $t(1) \leq t \leq t(2)$ $t(1) \leq t \leq t(2)$, $\forall x \in \lbrack 1;\ \ 2\rbrack$ $\forall x \in \lbrack 1;\ \ 2\rbrack$ suy ra $- 1 \leq t \leq 1.$ $- 1 \leq t \leq 1.$

Ta có $x^{2} + \frac{4}{x^{2}} = t^{2} + 4$ $x^{2} + \frac{4}{x^{2}} = t^{2} + 4$, $x^{4} + \frac{16}{x^{4}} = \left( x^{2} + \frac{4}{x^{2}} \right)^{2} - 8 = \left( t^{2} + 4 \right)^{2} - 8 = t^{4} + 8t^{2} + 8.$ $x^{4} + \frac{16}{x^{4}} = \left( x^{2} + \frac{4}{x^{2}} \right)^{2} - 8 = \left( t^{2} + 4 \right)^{2} - 8 = t^{4} + 8t^{2} + 8.$

Phương trình đã cho trở thành:

$t^{4} + 8t^{2} + 8 - 4\left( t^{2} + 4 \right) - 12t = m$ $t^{4} + 8t^{2} + 8 - 4\left( t^{2} + 4 \right) - 12t = m$

$\Leftrightarrow t^{4} + 4t^{2} - 12t = m + 8\ \ \ \ \ (*)$ $\Leftrightarrow t^{4} + 4t^{2} - 12t = m + 8\ \ \ \ \ (*)$.

Phương trình đã cho có nghiệm trong đoạn $\lbrack 1;\ \ 2\rbrack$ $\lbrack 1;\ \ 2\rbrack$ khi và chỉ khi phương trình $(*)$ có nghiệm trong $\lbrack - 1;\ \ 1\rbrack.$ $\lbrack - 1;\ \ 1\rbrack.$

Xét hàm số $y = f(t) = t^{4} + 4t^{2} - 12t$ $y = f(t) = t^{4} + 4t^{2} - 12t$ trên $\lbrack - 1;\ \ 1\rbrack.$ $\lbrack - 1;\ \ 1\rbrack.$

Đạo hàm $y' = 4t^{3} + 8t - 12$, $t \in ( - 1;\ \ 1)$ $t \in ( - 1;\ \ 1)$, $y' = 4(t - 1)\left( t^{2} + t + 3 \right) < 0$, $\forall t \in ( - 1;\ \ 1)$ $\forall t \in ( - 1;\ \ 1)$

Bảng biến thiên:

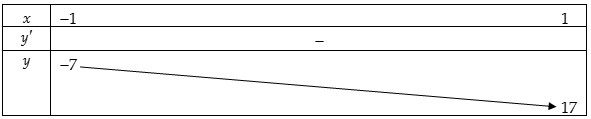
Do đó để phương trình đã cho có nghiệm trên $\lbrack 1;\ \ 2\rbrack$ $\lbrack 1;\ \ 2\rbrack$ thì $- 7 \leq m + 8 \leq 17$ $- 7 \leq m + 8 \leq 17$

$\Leftrightarrow - 15 \leq m \leq 9.$ $\Leftrightarrow - 15 \leq m \leq 9.$

Ví dụ 3. Có bao nhiêu giá trị nguyên của tham số m để phương trình $cos3x - cos2x + m\cos x = 1$ $cos3x - cos2x + m\cos x = 1$ có bảy nghiệm khác nhau thuộc khoảng $\left( - \frac{\pi}{2};2\pi \right)$ $\left( - \frac{\pi}{2};2\pi \right)$?

Hướng dẫn giải

Ta có:

$cos3x - cos2x + m\cos x = 1$ $cos3x - cos2x + m\cos x = 1$

$\Leftrightarrow \cos x\left( 4cos^{2}x - 2cosx - 3 + m \right) = 0$ $\Leftrightarrow \cos x\left( 4cos^{2}x - 2cosx - 3 + m \right) = 0$

$\Leftrightarrow \left\lbrack \begin{matrix} \cos x = 0 \\ 4cos^{2}x - 2cosx - 3 + m = 0 \end{matrix} \right.$ $\Leftrightarrow \left\lbrack \begin{matrix} \cos x = 0 \\ 4cos^{2}x - 2cosx - 3 + m = 0 \end{matrix} \right.$

$\cos x = 0 \Leftrightarrow x = \frac{\pi}{2} + k\pi;\left( k\mathbb{\in Z} \right)$ $\cos x = 0 \Leftrightarrow x = \frac{\pi}{2} + k\pi;\left( k\mathbb{\in Z} \right)$.

Do $x \in \left( - \frac{\pi}{2};2\pi \right)$ $x \in \left( - \frac{\pi}{2};2\pi \right)$ nên $x = \frac{\pi}{2};x = \frac{3\pi}{2}$ $x = \frac{\pi}{2};x = \frac{3\pi}{2}$.

$\Leftrightarrow 4cos^{2}x - 2cosx - 3 + m = 0\ \ \ (2)$ $\Leftrightarrow 4cos^{2}x - 2cosx - 3 + m = 0\ \ \ (2)$

Phương trình (1) có có bảy nghiệm khác nhau thuộc khoảng $\left( - \frac{\pi}{2};2\pi \right)$ $\left( - \frac{\pi}{2};2\pi \right)$ khi phương trình (2) có có năm nghiệm khác nhau thuộc khoảng $\left( - \frac{\pi}{2};2\pi \right)$ $\left( - \frac{\pi}{2};2\pi \right)$.

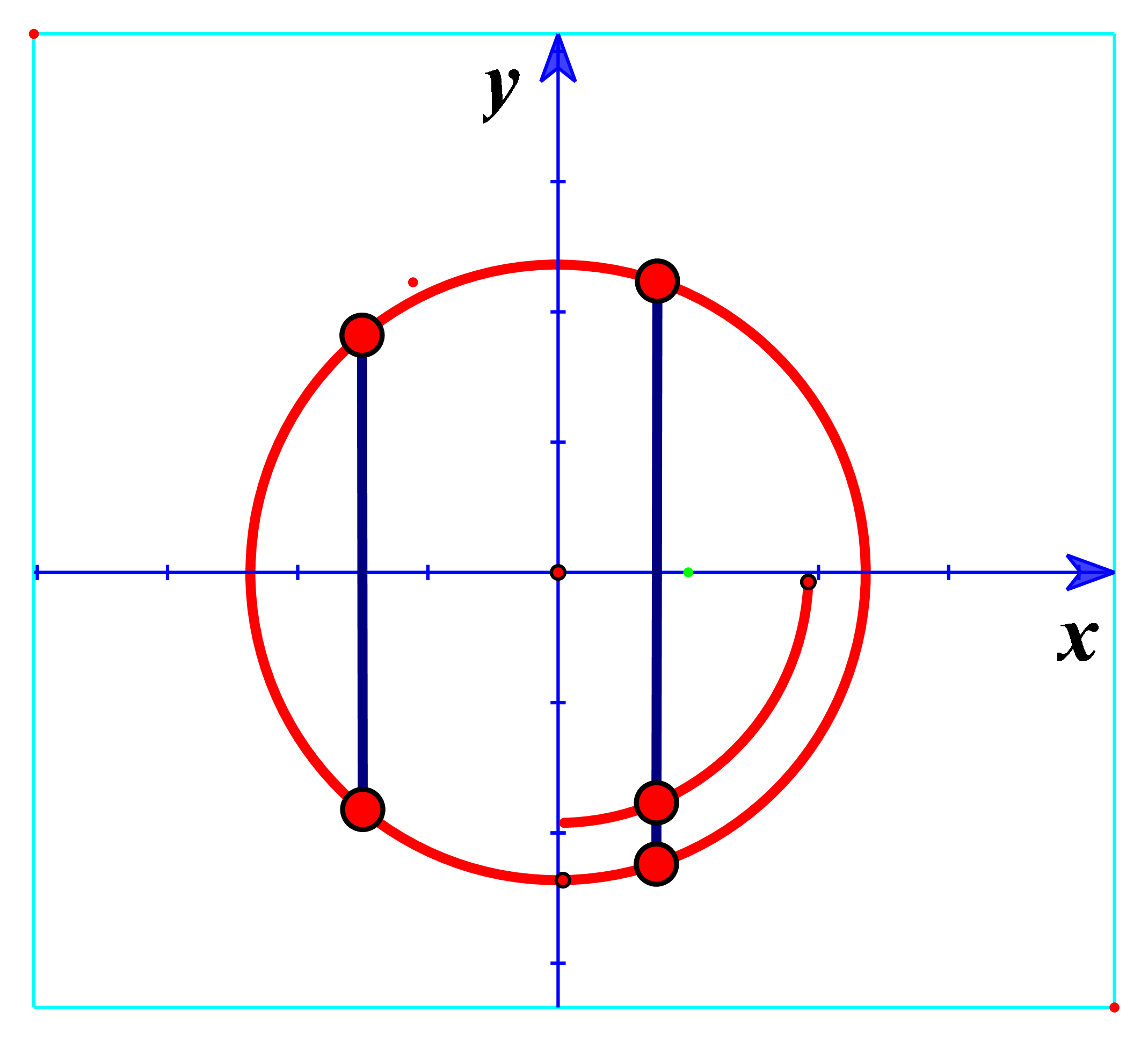
Khi đó phương trình (2) có hai nghiệm $- 1 < t_{1} < 0 < t_{2} < 1$ $- 1 < t_{1} < 0 < t_{2} < 1$ trong đó $t = \cos x$ $t = \cos x$.

Ta có: (2) $\Leftrightarrow 4t^{2} - 2t - 3 = - m$ $\Leftrightarrow 4t^{2} - 2t - 3 = - m$

Xét $f(t) = 4t^{2} - 2t - 3;t \in \lbrack - 1;1\rbrack$ $f(t) = 4t^{2} - 2t - 3;t \in \lbrack - 1;1\rbrack$

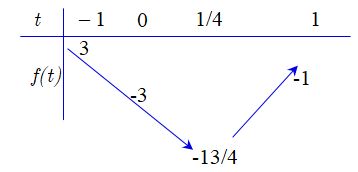
Khi đó $- 3 < - m < - 1 \Leftrightarrow 1 < m < 3$ $- 3 < - m < - 1 \Leftrightarrow 1 < m < 3$

Do $m\mathbb{\in Z}$ $m\mathbb{\in Z}$ nên $m = 2$.

C. Bài tập tự rèn luyện có hướng dẫn chi tiết

Bài tập 1. Tìm tất cả số thực của tham số $m$ để phương trình $2x - 1 = m(x - 1)$ có nghiệm thuộc đoạn $\lbrack - 1;\ 0\rbrack$ $\lbrack - 1;\ 0\rbrack$.

A. $m \leq \frac{3}{2}$ $m \leq \frac{3}{2}$. B. $m \geq 1$ $m \geq 1$. C. $1 \leq m \leq \frac{3}{2}$ $1 \leq m \leq \frac{3}{2}$. D. $1 \leq m \leq 2$ $1 \leq m \leq 2$.

Bài tập 2. Tìm tất cả các giá trị của $m$ để phương trình $sin^{4}x + cos^{4}x + cos^{2}4x = m$ $sin^{4}x + cos^{4}x + cos^{2}4x = m$ có bốn nghiệm phân biệt thuộc đoạn $\left\lbrack - \frac{\pi}{4};\frac{\pi}{4} \right\rbrack$ $\left\lbrack - \frac{\pi}{4};\frac{\pi}{4} \right\rbrack$.

A. $m \leq \frac{47}{64}$ $m \leq \frac{47}{64}$ hoặc $m \geq \frac{3}{2}$ $m \geq \frac{3}{2}$. B. $\frac{47}{64} < m < \frac{3}{2}$ $\frac{47}{64} < m < \frac{3}{2}$.

C. $\frac{47}{64} < m \leq \frac{3}{2}$ $\frac{47}{64} < m \leq \frac{3}{2}$. D. $\frac{47}{64} \leq m \leq \frac{3}{2}$ $\frac{47}{64} \leq m \leq \frac{3}{2}$.

Bài tập 3. Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f\left( 2\left| \sin x \right| \right) = f\left( \frac{m}{2} \right)$ $f\left( 2\left| \sin x \right| \right) = f\left( \frac{m}{2} \right)$ có đúng 12 nghiệm phân biệt thuộc đoạn $\lbrack - \pi;\ 2\pi\rbrack$ $\lbrack - \pi;\ 2\pi\rbrack$?

A. $3.$ B. $4.$ C. $2.$ D. $5.$

Bài tập 4. Tìm các giá trị thực của tham số $m$ để phương trình $\left( \sin x - 1 \right)\left( cos^{2}x - \cos x + m \right) = 0$ $\left( \sin x - 1 \right)\left( cos^{2}x - \cos x + m \right) = 0$ có đúng 5 nghiệm thuộc đoạn $\lbrack 0;2\pi\rbrack$ $\lbrack 0;2\pi\rbrack$.

A. $0 \leq m < \frac{1}{4}$ $0 \leq m < \frac{1}{4}$. B. $- \frac{1}{4} < m \leq 0$ $- \frac{1}{4} < m \leq 0$. C. $0 < m < \frac{1}{4}$ $0 < m < \frac{1}{4}$. D. $- \frac{1}{4} < m < 0$ $- \frac{1}{4} < m < 0$

Bài tập 5. Gọi $K$ là tập hợp tất cả các giá trị của tham số $m$ để phương trình $sin2x + \sqrt{2}\sin\left( x + \frac{\pi}{4} \right) - 2 = m$ $sin2x + \sqrt{2}\sin\left( x + \frac{\pi}{4} \right) - 2 = m$ có đúng hai nghiệm thuộc khoảng $\left( 0;\ \frac{3\pi}{4} \right)$ $\left( 0;\ \frac{3\pi}{4} \right)$. Hỏi $K$ là tập con của tập hợp nào dưới đây?

A. $\left( - \frac{\sqrt{2}}{2};\ \frac{\sqrt{2}}{2} \right\rbrack$ $\left( - \frac{\sqrt{2}}{2};\ \frac{\sqrt{2}}{2} \right\rbrack$. B. $\left( 1 - \sqrt{2};\ \sqrt{2} \right)$ $\left( 1 - \sqrt{2};\ \sqrt{2} \right)$. C. $\left( - \sqrt{2};\ \frac{\sqrt{2}}{2} \right)$ $\left( - \sqrt{2};\ \frac{\sqrt{2}}{2} \right)$. D. $\left( - \frac{\sqrt{2}}{2};\ \sqrt{2} \right\rbrack$ $\left( - \frac{\sqrt{2}}{2};\ \sqrt{2} \right\rbrack$.

📖 Toàn bộ nội dung, bài tập và lời giải đã được tổng hợp trong tài liệu tải về.

---------------------------------------------------

Nắm vững phương pháp tìm m để phương trình có nghiệm trong khoảng, đoạn cho trước sẽ giúp học sinh chủ động xử lý các bài toán tham số m một cách linh hoạt. Khi hiểu rõ bản chất bài toán hàm số và điều kiện nghiệm, bạn sẽ dễ dàng chinh phục các câu hỏi vận dụng trong đề THPT Quốc gia môn Toán và các kỳ kiểm tra quan trọng.

Xem thử Tải về

Chọn file muốn tải về: