Tìm tham số m để đồ thị hàm số cắt trục hoành tại một điểm duy nhất
Dạng toán đồ thị hàm số cắt trục hoành ôn thi THPT Quốc gia
Trong quá trình ôn thi THPT Quốc gia môn Toán, các bài toán tìm tham số m để đồ thị hàm số cắt trục hoành tại một điểm duy nhất luôn xuất hiện với tần suất cao và có tính phân loại rõ rệt. Dạng toán này yêu cầu học sinh nắm vững mối liên hệ giữa nghiệm phương trình và hình dạng đồ thị, từ đó xác định chính xác điều kiện của tham số m. Bài viết sau sẽ giúp bạn tiếp cận dạng toán này nhanh – đúng – hiệu quả, phù hợp cả luyện thi và ôn tập chuyên sâu.
A. Cách tìm m để đồ thị hàm số cắt trục hoành tại 1 điểm
Cho phương trình 
\(f(x) = f(m)\) \((*)\)
Phương pháp:
- Bước 1: Cô lập tham số \(m\) và đưa về dạng \(f(x) = f(m)\).
- Bước 2: Khảo sát sự biến thiên của hàm số \(f(x)\) trên \(D\).
- Bước 3: Dựa vào bảng biến thiên để sác định giá trị tham số \(f(m)\) sao cho đường thẳng \(y = f(m)\) nằm ngang vắt đồ thị hàm số \(y = f(x)\).
- Bước 4: Kết luận giá trị của \(f(m)\) để phương trình \(f(x) = f(m)\) có nghiệm trên \(D\).
B. Bài tập minh họa tìm m để đồ thị hàm số cắt trục hoành tại 1 điểm
Ví dụ 1. Tìm tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = x^{3} + mx + 2\) cắt trục hoành tại một điểm duy nhất.
Hướng dẫn giải
Phương trình hoành độ giao điểm của đồ thị \((C)\) và trục hoành là: \(x^{3} + mx + 2 = 0 \Leftrightarrow m = -
\frac{2}{x} - x^{2}\) (do \(x =
0\) không là nghiệm của phương trình).
Xét hàm số \(g(x) = - \frac{2}{x} -
x^{2}\) có: \(D\mathbb{= R}\backslash\left\{ 0
\right\}\).
\(g'(x) = \frac{2}{x^{2}} -
2x\)=> \(g'(x) = 0 \Leftrightarrow x =
1\).
Bảng biến thiên:
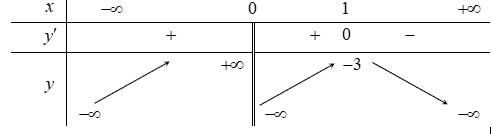
Dựa vào đồ thị ta có, để đồ thị hàm số \(y
= x^{3} + mx + 2\) cắt trục hoành tại một điểm duy nhất thì \(m > - 3\).
Ví dụ 2. Tập hợp tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = x^{2} + m\sqrt{4 - x^{2}} + m - 7\) có điểm chung với trục hoành là \(\lbrack a;\
b\rbrack\) (với \(a;\ b\mathbb{\in
R}\)). Tính giá trị của \(S = 2a +
b\).
Hướng dẫn giải
Tập xác định của hàm số: \(D = \lbrack -
2;\ 2\rbrack\).
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = x^{2} + m\sqrt{4 - x^{2}} + m - 7\) và trục hoành là
\(x^{2} + m\sqrt{4 - x^{2}} + m - 7 =
0\)
\(\Leftrightarrow m\left( \sqrt{4 - x^{2}}
+ 1 \right) = 7 - x^{2}\)
\(\Leftrightarrow m = \frac{7 -
x^{2}}{\sqrt{4 - x^{2}} + 1}\ \ \ (1)\).
Đặt \(t = \sqrt{4 - x^{2}}\), \(t \in \lbrack 0;2\rbrack\), phương trình \((1)\) trở thành \(m = \frac{t^{2} + 3}{t + 1}\ \ \ (2)\).
Đồ thị hàm số đã cho có điểm chung với trục hoành khi và chỉ khi phương trình \((2)\) có nghiệm \(t \in \lbrack 0;2\rbrack\).
Xét hàm số \(f(t) = \frac{t^{2} + 3}{t +
1}\) trên \(\lbrack
0;2\rbrack\).
Hàm số \(f(t)\) liên tục trên \(\lbrack 0;2\rbrack\).
Ta có \(f^{'(t)} = \frac{t^{2} + 2t -
3}{(t + 1)^{2}}\), \(f^{'(t)} = 0
\Leftrightarrow \left\lbrack \begin{matrix}
t = 1 \in (0;2) \\
t = - 3 \notin (0;2)
\end{matrix} \right.\).
\(f(0) = 3\), \(f(1) = 2\), \(f(2) = \frac{7}{3}\).
Do đó \(\min_{\lbrack 0;2\rbrack}f(t) =
2\) và \(\max_{\lbrack 0;2\rbrack}f(t)
= 3\).
Bởi vậy, phương trình \((2)\) có nghiệm \(t \in \lbrack 0;2\rbrack\) khi và chỉ khi:
\(\min_{\lbrack 0;2\rbrack}f(t)
\leq m \leq \max_{\lbrack 0;2\rbrack}f(t) \Leftrightarrow 2 \leq m \leq
3\).
Từ đó suy ra \(a = 2\), \(b = 3\), nên \(S
= 2a + b = 2.2 + 3 = 7\).
C. Bài tập vận dụng có hướng dẫn chi tiết
Bài tập 1. Cho hàm số \(y = x^{3} + mx -
2\). Tìm tất cả các điều kiện của \(m\) để đồ thị hàm số cắt trục hoành tại một điểm duy nhất.
A. \(m < - 3\). B. \(m < 3\). C. \(m > - 3\). D. \(m > 3\).
Bài tập 2. Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y = \left( {m + 1} \right){x^4} - 2\left( {2m - 3} \right){x^2} + 6m + 5\) cắt trục hoành tại 4 điểm phân biệt có các hoành độ \({x_1};{x_2};{x_3};{x_4}\) thỏa mãn \({x_1} < {x_2} < {x_3} < 1 < {x_4}\)?
A. \(m \in \left( { - 1; - \frac{5}{6}} \right)\) B. \(m \in \left( { - 3; - 1} \right)\)
C. \(m \in \left( { - 3;1} \right)\) D. \(m \in \left( { - 4; - 1} \right)\)
Bài tập 3. Tập hợp tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = x^{2} + m\sqrt{4 - x^{2}} + m - 7\) có điểm chung với trục hoành là \(\lbrack a;\
b\rbrack\) (với \(a;\ b\mathbb{\in
R}\)). Tính giá trị của \(S = a +
b\).
A. \(S = \frac{13}{3}\). B. \(S = 5\). C. \(S =
3\). D. \(S =
\frac{16}{3}\).
Bài tập 4. Phương trình \(x^{3} - 3mx + 2 =
0\) có một nghiệm duy nhất khi điều kiện của \(m\) là
A. \(m > 1\). B. \(m > - 1\). C. \(m < - 2\). D. \(m < 1\).
🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.
-----------------------------------------------------------------
Việc thành thạo bài toán đồ thị hàm số cắt trục hoành tại một điểm duy nhất không chỉ giúp học sinh xử lý nhanh các câu hỏi tham số m mà còn nâng cao tư duy hình học – đại số tổng hợp. Hy vọng qua bài viết này, bạn đã nắm được hướng tiếp cận đúng và tự tin áp dụng vào các đề thi THPT Quốc gia môn Toán cũng như các bài kiểm tra nâng cao.
