Bài toán Thực tế tối ưu diện tích và thể tích (Có lời giải chi tiết)
Dạng bài tối ưu diện tích thể tích thường gặp trong đề thi THPT Quốc gia
Trong quá trình ôn luyện Toán THPT Quốc gia, các dạng bài toán thực tế về tối ưu diện tích và thể tích luôn xuất hiện với tần suất cao, đòi hỏi học sinh không chỉ nắm vững kiến thức đạo hàm mà còn biết cách vận dụng linh hoạt vào các tình huống hình học quen thuộc. Những bài toán này thường gắn liền với việc thiết kế, xây dựng, đóng gói hay sản xuất, giúp Toán học trở nên gần gũi và thiết thực hơn.
A. Cách giải bài toán tối ưu thể tích
Xác định mối quan hệ các đại lượng (đại lượng đề bài cho và đại lượng cần tìm giá trị lớn nhất, nhỏ nhất).
-
Quy bài toán thực tế vê bài toán tìm giá trị lớn nhất, nhỏ nhất của hàm số.
-
Lập bảng biến thiên tìm giá trị lớn nhất nhỏ nhất của đại lượng cần xét.
B. Bài tập minh họa tính tối ưu diện tích thể tích hình khối
Ví dụ 1. Cho một tấm nhôm hình vuông cạnh 
\(1\ (m)\)như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng \(x\ (m)\), sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp.
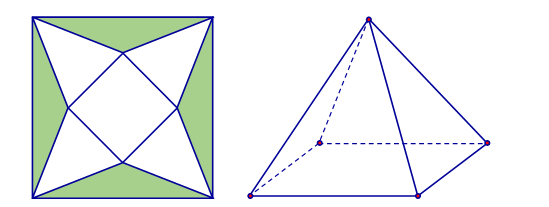
Tìm giá trị của \(x\)để khối chóp nhận được có thể tích lớn nhất.
A. \(x = \frac{\sqrt{2}}{4}\). B. \(x = \frac{\sqrt{2}}{3}\). C. \(x = \frac{2\sqrt{2}}{5}\). D. \(x = \frac{1}{2}\)
Hướng dẫn giải
Chọn C.
Kí hiệu hình vẽ như sau:
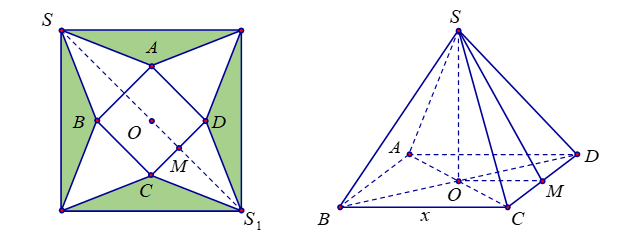
Từ hình vuông ban đầu ta tính được \(OM =
\frac{x}{2},\ S_{1}M = S_{1}O - OM = \frac{\sqrt{2} - x}{2}\). (\(0 < x < \sqrt{2}\))
Khi gấp thành hình chóp \(S.ABCD\) thì \(S_{1} \equiv S\) nên ta có \(SM = S_{1}M\).
Từ đó \(SO = \sqrt{SM^{2} - OM^{2}} =
\frac{\sqrt{2 - 2\sqrt{2}x}}{2}\) (Điều kiện \(0 < x < \frac{\sqrt{2}}{2}\))
Thể tích khối chóp \(S.ABCD\):
\(V_{S.ABCD} = \frac{1}{3}S_{ABCD}.SO =
\frac{1}{6}x^{2}\sqrt{2 - 2\sqrt{2}x} = \frac{1}{6}\sqrt{2x^{4} -
2\sqrt{2}x^{5}}\).
Ta thấy \(V_{SABCD}\) lớn nhất khi \(f(x) = 2x^{4} - 2\sqrt{2}x^{5},0 < x <
\frac{\sqrt{2}}{2}\) đạt giá trị lớn nhất
Ta có:
\(f'(x) = 8x^{3} -
10\sqrt{2}x^{4} = 2x^{3}\left( 4 - 5\sqrt{2}x \right)\)
\(f'(x) = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = \frac{2\sqrt{2}}{5}
\end{matrix} \right.\)
Bảng biến thiên:
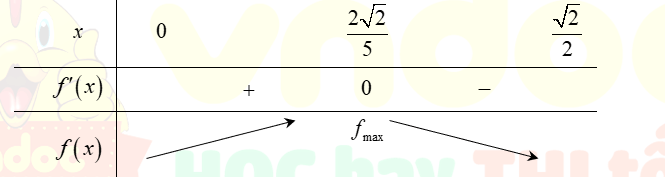
Vậy: \(V_{S.ABCD}\) lớn nhất khi và chỉ khi \(x = \frac{2\sqrt{2}}{5}\)
Ví dụ 2. Cắt ba góc của một tam giác đều cạnh bằng \(a\) các đoạn bằng \(x,\ \left( 0 < x < \frac{a}{2}
\right)\)phần còn lại là một tam giác đều bên ngoài là các hình chữ nhật, rồi gấp các hình chữ nhật lại tạo thành khối lăng trụ tam giác đều như hình vẽ.
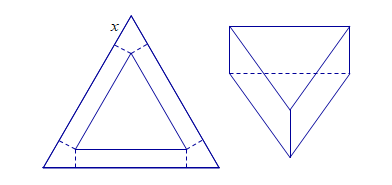
Tìm độ dài \(x\) để thể tích khối lăng trụ lớn nhất.
A. \(\frac{a}{3}\). B. \(\frac{a}{4}\). C. \(\frac{a}{5}\). D. \(\frac{a}{6}\).
Hướng dẫn giải
Chọn D
Hình vẽ minh họa:
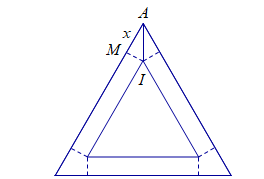
Xét tam giác \(AMI\) như hình vẽ, đặt \(AM = x > 0,\widehat{MAI} =
30{^\circ}\) \(\Rightarrow MI =
\frac{x}{\sqrt{3}}\)
Lăng trụ tam giác đều có cạnh đáy \(a -
2x\), \(\left( 0 < x <
\frac{a}{2} \right)\), chiều cao \(\frac{x}{\sqrt{3}}\)nên thể tích khối lăng trụ là:
\(V = \frac{(a -
2x)^{2}\sqrt{3}}{4}.\frac{x}{\sqrt{3}} = \frac{a^{2}x - 4ax^{2} +
4x^{3}}{4}\)
Ta cần tìm \(x \in \left( 0;\ \frac{a}{2}
\right)\)để thể tích \(V\) đạt giá trị lớn nhất.
Xét \(f(x) = a^{2}x - 4ax^{2} +
4x^{3}\), có
\(f'(x) = 12x^{2} -
8ax + a^{2} = 0 \Rightarrow \left\lbrack \begin{matrix}
x = \frac{a}{6} \\
x = \frac{a}{2}(l)
\end{matrix} \right.\)
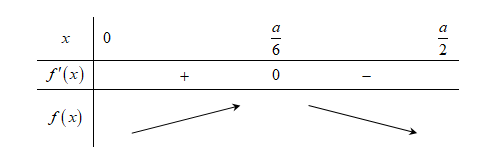
Từ bảng biến thiên suy ra thể tích \(V\)đạt giá trị lớn nhất khi \(x = \frac{a}{6}\).
Ví dụ 3. Từ một tấm tôn hình chữ nhật có kích thước \(40\)cm và \(60\) cm người ta cắt bỏ bốn hình vuông ở bốn góc để gập lại được một cái hộp không nắp.
Để thể tích của hộp đó lớn nhất thì cạnh hình vuông cắt bỏ có giá trị gần với giá trị nào sau đây?
A. \(7,85\)cm. B. \(15\)cm. C. \(3,92\)cm. D. \(18\)cm.
Hướng dẫn giải
Chọn A
Hình vẽ minh họa:
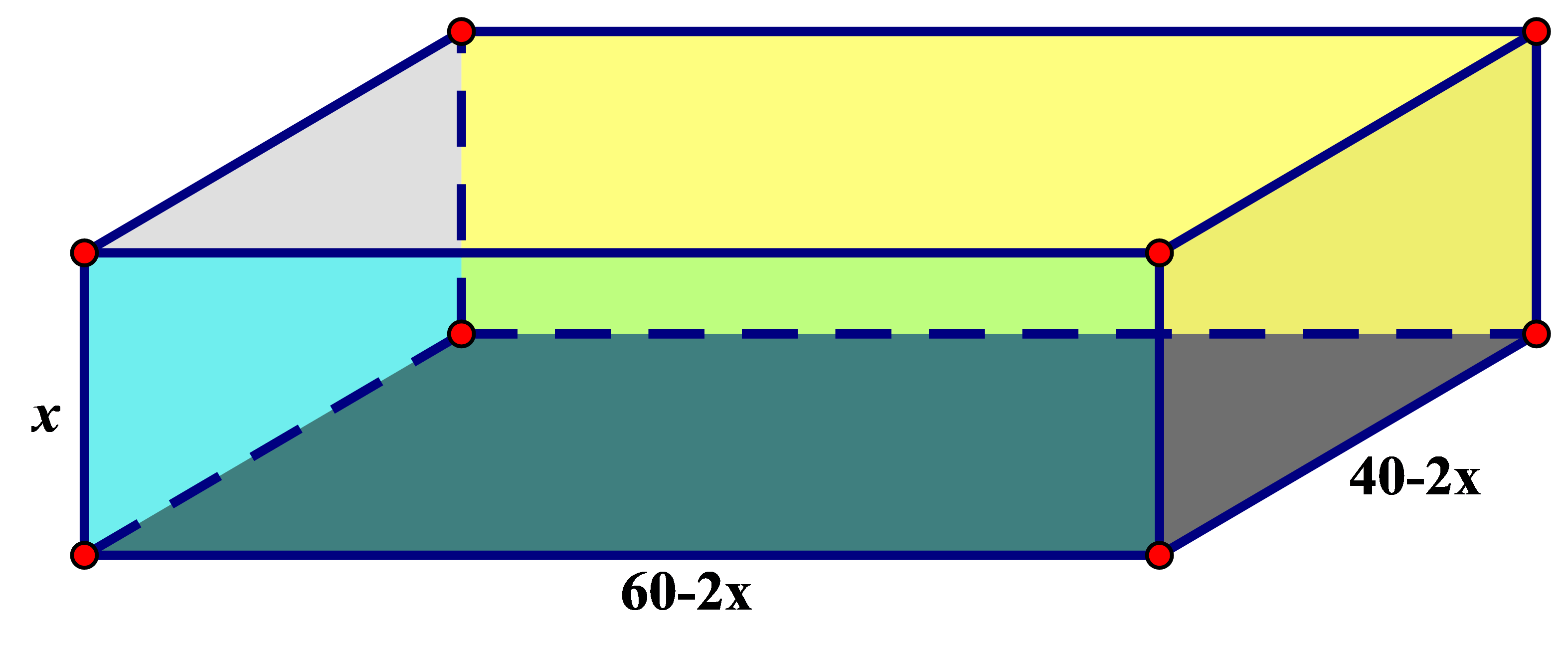
Đặt cạnh hình vuông cắt bỏ là \(x\), \((0 < x < 20)\).
Khi đó thể tích hình hộp thu được là \(V =
x(60 - 2x)(40 - 2x)\)
\(\Rightarrow V' = 4\left( 3x^{2} -
100x + 600 \right)\)
\(\Rightarrow V' = 0 \Leftrightarrow x
= \frac{50 \pm 10\sqrt{7}}{3}\).
Do \(0 < x < 20\)nên \(x = \frac{50 - 10\sqrt{7}}{3} =
x_{0}\).
Bảng biến thiên:
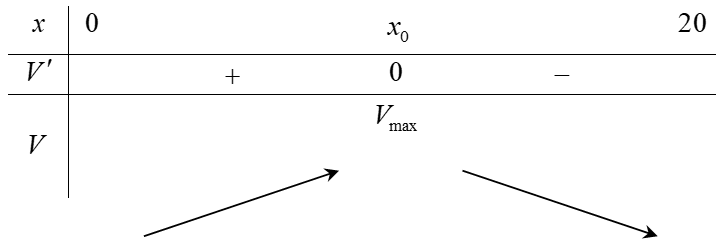
Vậy thể tích của khối hộp thu được lớn nhất khi \(x = \frac{50 - 10\sqrt{7}}{3} \approx
7,85\)cm.
C. Bài tập vận dụng có đáp án chi tiết
Bài tập 1. Bạn An là một học sinh lớp 12, bố bạn là một thợ hàn. Bố bạn định làm một chiếc thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:
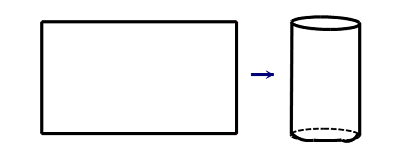
Bằng kiến thức đã học em giúp bố bạn chọn mảnh tôn để làm được chiếc thùng có thể tích lớn nhất, khi đó chiều dài, rộng của mảnh tôn lần lượt là bao nhiêu?
Bài tập 2. Với một miếng tôn hình tròn có bán kính bằng R = 6cm. Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ).
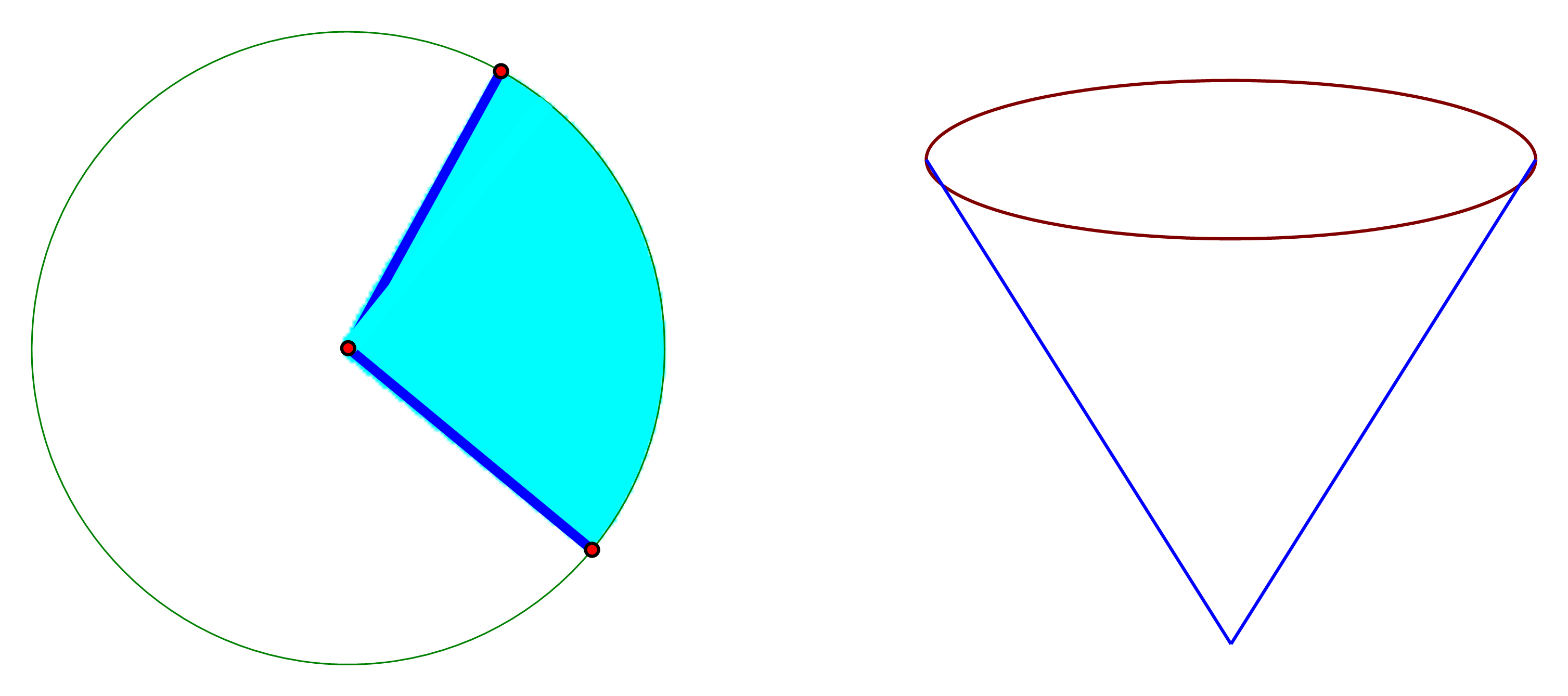
Hình nón có thể tích lớn nhất khi người ta cắt cung tròn của hình quạt bằng bao nhiêu?
Bài tập 3. Cho hình chữ nhật có diện tích bằng \(100(cm^{2})\). Hỏi mỗi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất?
A. \(10cm \times 10cm\) B. \(20cm \times 5cm\) C. \(25cm \times 4cm\) D. Đáp án khác
Bài tập 4. Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(30cm\) người ta gấp theo các đoạn \(MN,PQ\) sao cho \(AD,BC\) trùng nhau để tạo thánh một hình lăng trụ bị khuyết 2 đáy như hình minh họa dưới đây
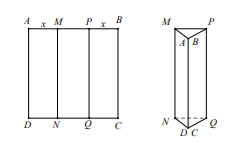
Đề thể tích của khối lăng trụ tương ứng với hình lăng trụ tạo thành là lớn nhất thì giá trị của \(x\)bằng
A. \(8\ cm\). B. \(9\ cm\). C. \(10\
cm\). D. \(5\ cm\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
-------------------------------------------------
Việc thành thạo bài toán tối ưu diện tích và thể tích trong thực tế không chỉ giúp học sinh ghi điểm ở các câu vận dụng mà còn tạo nền tảng vững chắc để xử lý những bài toán nâng cao trong đề thi THPT Quốc gia. Thông qua hệ thống bài tập có lời giải chi tiết, người học sẽ rèn luyện được kỹ năng lập mô hình toán học, xét cực trị và đưa ra kết luận chính xác.
Hy vọng nội dung bài viết sẽ là tài liệu tham khảo hữu ích, đồng hành cùng bạn trong quá trình ôn luyện và chinh phục môn Toán THPT Quốc gia với kết quả cao nhất.
