Bài toán thực tế tối ưu Quãng đường – Phương pháp giải chuẩn nhất
Cách lập hàm và tìm GTLN GTNN trong bài toán quãng đường
Trong các dạng toán ứng dụng của chương trình Toán học phổ thông, bài toán thực tế tối ưu quãng đường là chủ đề quen thuộc, thường xuất hiện trong các tình huống liên quan đến chuyển động, giao thông, vận chuyển và sắp xếp lộ trình. Để giải chính xác dạng toán này, học sinh cần biết cách lập hàm số phù hợp và vận dụng đạo hàm để tìm GTLN – GTNN.
A. Bài tập minh họa tính tối ưu quãng đường
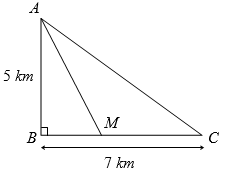
Ví dụ 1. Một ngọn hải đăng được đặt tại vị trí 
\(A\)cách bờ biển một khoảng \(AB = 5\ km\). Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) một khoảng \(7\ km\). Người canh hải đăng có thể chèo đò từ \(A\) đến địa điểm \(M\)trên bờ biển với vận tốc \(4\ km/h\), rồi đi bộ đến \(C\) với vận tốc \(6\ km/h\).
Hỏi cần đặt vị trí của \(M\) cách \(B\) một khoảng bằng bao nhiêu km để người đó đến kho nhanh nhất?
A. \(5,5\ km.\) B. \(2\sqrt{5}\ km.\) C. \(\sqrt{5}\ km.\) D. \(4,5\ km\).
Hướng dẫn giải
Chọn B
Gọi \(BM = x(km);\ (0 \leq x \leq
7)\)
Khi đó \(AC = \sqrt{x^{2} + 25}\
(km)\)
Thời gian người đó đi từ A đến M rồi đến C là: \(f(x) = \frac{\sqrt{x^{2} + 25}}{4} + \frac{7 -
x}{6}\)
Ta có: \(f'(x) = \frac{x}{4\sqrt{x^{2}
+ 25}} - \frac{1}{6}\)
Xét \(f'(x) = 0 \Leftrightarrow 6x =
4\sqrt{x^{2} + 25} \Leftrightarrow x = 2\sqrt{5} \in \lbrack
0;7\rbrack\)
\(f(0) = \frac{29}{12}\) ,\(f(7) = \frac{\sqrt{74}}{4}\),\(f\left( 2\sqrt{5} \right) = \frac{5\sqrt{5}}{12} +
\frac{7}{6}\).
Để đến kho nhanh nhất thì \(x =
2\sqrt{5}\).
Lưu ý:
Giải bằng phương pháp trắc nghiệm
Nhập biểu thức \(f(x) = \frac{\sqrt{x^{2} +
25}}{4} + \frac{7 - x}{6}\)vào máy tính
Nhấn phím CALC thay lần lượt 4 đáp án A, B, C, D
Chọn kết quả nhỏ nhất.
Ví dụ 2. Một cái hồ rộng có hình chữ nhật. Tại một góc nhỏ của hồ người ta đóng một cái cọc ở vị trí \(K\)cách bờ \(AB\) là \(1m\) và cách bờ \(AC\) là \(8m\), rồi dùng một cây sào ngăn một góc nhỏ của hồ để thả bèo (như hình vẽ).
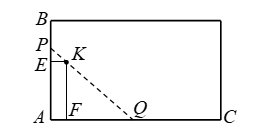
Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào \(2\)bờ \(AB\), \(AC\) và cây cọc \(K\) (bỏ qua đường kính của sào).
A. \(\frac{5\sqrt{65}}{4}\). B. \(5\sqrt{5}\). C. \(9\sqrt{2}\). D. \(\frac{5\sqrt{71}}{4}\).
Hướng dẫn giải
Chọn B
Đặt \(AP = a\),\(AQ = b\) \((a,b
> 0)\).
Gọi \(E\) và \(F\) lần lượt là hình chiếu vuông góc của \(K\)xuống \(AB\) và \(AC\). Suy ra \(KE
= 1\), \(KF = 8\).
Ta có:
\(\frac{KE}{AQ} =
\frac{PK}{PQ}\), \(\frac{KF}{AP} =
\frac{QK}{PQ} \Rightarrow \frac{KF}{AP} + \frac{KE}{AQ} = 1\) hay \(\frac{8}{a} + \frac{1}{b} = 1\).
(Hoặc có thể dùng phép tọa độ hóa: Gán \(A
= (0;0)\),\(P = (0;a)\),\(Q = (b;0)\).
Khi đó \(K = (1;8)\).
Phương trình đường thẳng \(PQ:\frac{x}{b} +
\frac{y}{a} = 1\) (Vì \(PQ\) đi qua \(K\)nên \(\frac{1}{b} + \frac{8}{a} = 1\))
Cách 1:
Ta có: \(PQ^{2} = a^{2} + b^{2}\). Vì \(\frac{8}{a} + \frac{1}{b} = 1 \Rightarrow
\frac{8k}{a} + \frac{k}{b} = k\) \(\forall k > 0\).
\(a^{2} + b^{2} + k = \left( a^{2} +
\frac{8k}{a} \right) + \left( b^{2} + \frac{k}{b} \right)\) \(= \left( a^{2} + \frac{4k}{a} + \frac{4k}{a}
\right) + \left( b^{2} + \frac{k}{2b} + \frac{k}{2b} \right) \geq
3\sqrt[3]{16k^{2}} + 3\sqrt[3]{\frac{k^{2}}{4}}\).
Suy ra \(PQ\) nhỏ nhất \(\Leftrightarrow a^{2} + b^{2}\) nhỏ nhất \(\Leftrightarrow \left\{ \begin{matrix}
a^{2} = \frac{4k}{a} \\
b^{2} = \frac{k}{2b} \\
\frac{8}{a} + \frac{1}{b} = 1
\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}
k = 250 \\
a = 10 \\
b = 5
\end{matrix} \right.\).
Vậy giá trị nhỏ nhất của \(PQ\) là \(\sqrt{a^{2} + b^{2}} = \sqrt{125}\) \(= 5\sqrt{5}\).
Từ đó suy ra chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào \(2\) bờ \(AB\), \(AC\)và cây cọc \(K\) là \(5\sqrt{5}\).
Cách 2:
Vì \(\frac{8}{a} + \frac{1}{b} = 1
\Rightarrow b = \frac{a}{a - 8}\) với \(a > 8\).
Khi đó \(PQ^{2} = a^{2} + b^{2} = a^{2} +
\left( \frac{a}{a - 8} \right)^{2}\) với \(a > 8\).
Xét hàm số \(f(a) = a^{2} + \left(
\frac{a}{a - 8} \right)^{2}\)với \(a
> 8\).
Ta có \(f'(a) = 2a + \frac{2a}{a -
8}.\frac{- 8}{(a - 8)^{2}} = \frac{2a\left\lbrack (a - 8)^{3} - 8
\right\rbrack}{(a - 8)^{3}}\), \(f'(a) = 0 \Rightarrow a = 10\).
Bảng biến thiên của \(f(a)\):
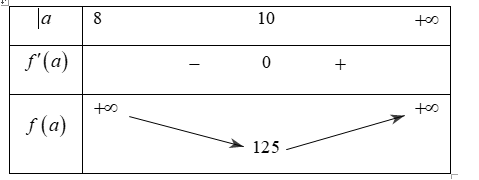
Vậy GTNN của \(f(a)\) là \(125\) khi \(a =
10\).
Từ đó suy ra chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào \(2\)bờ \(AB\), \(AC\) và cây cọc \(K\)là \(\sqrt{125} = 5\sqrt{5}\).
B. Bài tập vận dụng có đáp án chi tiết
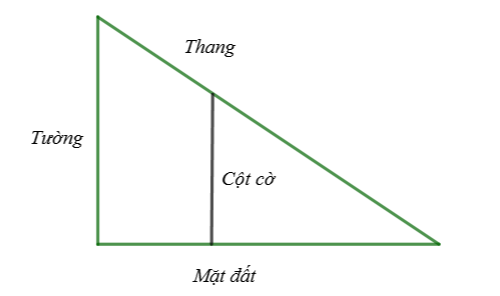
Bài tập 1. Tính chiều dài nhỏ nhất của cái thang để nó có thể dựa vào tường và mặt đất, bắc qua cột đỡ cao \(4m\). Biết cột đỡ song song và cách tường \(0,5m\), mặt phẳng chứa tường vuông góc với mặt đất – như hình vẽ, bỏ qua độ dày của cột đỡ.
Bài tập 2. Anh T đang ở khách sạn \(A\) bên bờ biển, cô cần đi du lịch đến hòn đảo \(C\). Biết rằng khoảng cách từ đảo \(C\) đến bờ biển là \(10\ \ km\), khoảng cách từ khách sạn \(A\) đến điểm \(B\) trên bờ gần đảo \(C\) là \(50\ \
km\). Từ khách sạn \(A\), anh T có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy để đến hòn đảo \(C\) (như hình vẽ bên).
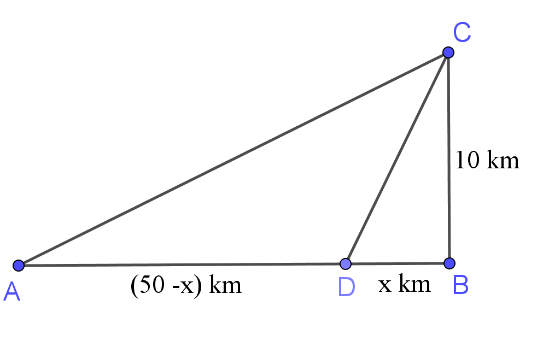
Biết rằng chi phí đi đường thủy là \(5\) USD/km, chi phí đi đường bộ là \(3\) USD/km. Hỏi anh T phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
A. \(\frac{15}{2}\ (km)\). B. \(\frac{85}{2}\ (km)\). C. \(50(km)\). D. \(10\sqrt{26}\ (km)\).
Bài tập 3. Một công ty muốn làm một đường ống dẫn từ một điểm \(A\) trên bờ đến một điểm \(B\) trên một hòn đảo. Hòn đảo cách bờ biển \(6km\). Giá để xây đường ống trên bờ là \(50.000\ USD\) mỗi \(km\), và \(130.000USD\) mỗi \(km\) để xây dưới nước. \(B’\) là điểm trên bờ biển sao cho \(BB’\) vuông góc với bờ biển. Khoảng cách từ \(A\) đến \(B’\) là \(9km\).
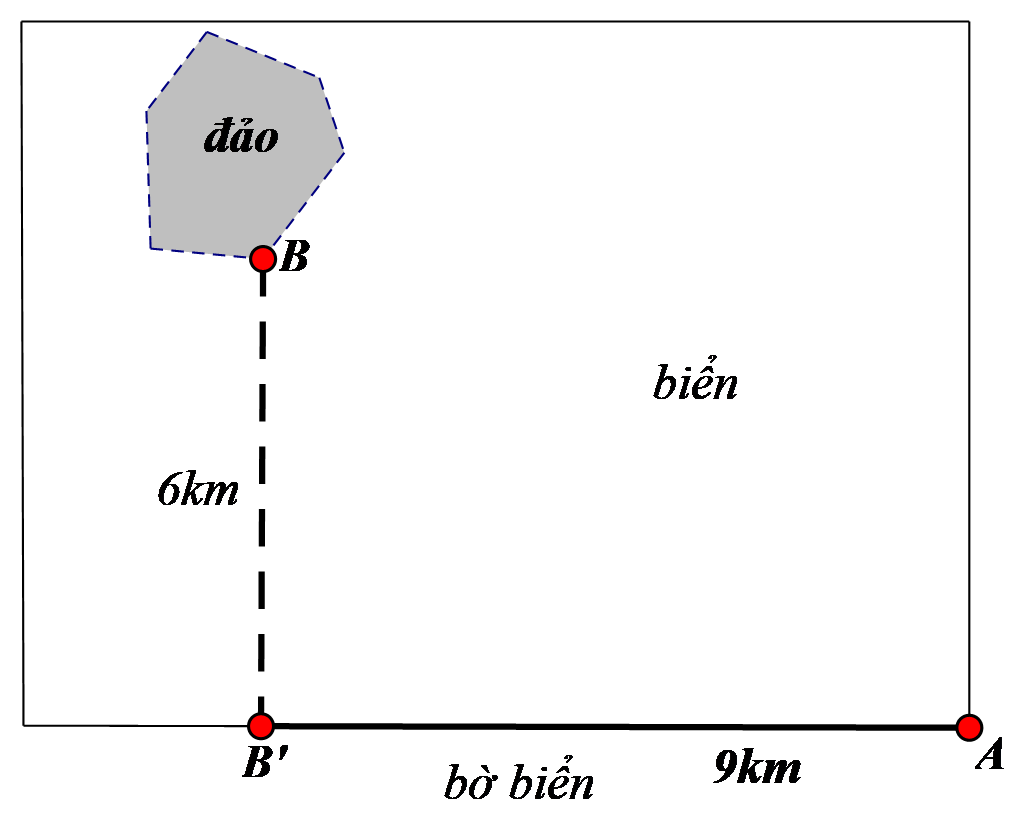
Vị trí \(C\) trên đoạn \(AB’\) sao cho khi nối ống theo \(ACB\) thì số tiền ít nhất. Khi đó \(C\) cách \(A\) một đoạn bằng:
A. \(6.5km\). B. \(6km\). C. \(0km\). D. \(9km\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu!
-----------------------------------------------------
Việc hiểu đúng và áp dụng thành thạo phương pháp giải bài toán tối ưu quãng đường sẽ giúp học sinh xử lý hiệu quả các bài toán thực tế trong đề kiểm tra và kỳ thi quan trọng. Thông qua quá trình lập hàm, xét đạo hàm và kết luận GTLN – GTNN, người học không chỉ nâng cao kỹ năng giải toán mà còn rèn luyện tư duy logic và khả năng mô hình hóa tình huống.
Hy vọng nội dung bài viết sẽ là tài liệu tham khảo đáng tin cậy, hỗ trợ bạn học tốt các dạng toán ứng dụng và đạt kết quả cao trong môn Toán.
