VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Bài tập Tính phương sai và độ lệch chuẩn Có đáp án (Tiếp)

Ôn thi THPT Quốc Gia môn Toán

Trắc nghiệm Toán 12: Phương sai và độ lệch chuẩn - Có hướng dẫn chi tiết

Chào mừng các bạn đến với chuyên đề Bài tập tính phương sai và độ lệch chuẩn có đáp án – một phần quan trọng trong chương trình Thống kê và Xác suất lớp 12 và ôn thi THPT Quốc gia. Trong bài viết này, bạn sẽ được luyện tập với các dạng bài tập tiêu biểu, từ cơ bản đến nâng cao, kèm lời giải chi tiết. Đây là tài liệu hữu ích giúp bạn hiểu rõ bản chất của phương sai và độ lệch chuẩn, cũng như cách áp dụng công thức một cách chính xác và nhanh chóng trong quá trình làm bài.

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 28 câu
Điểm số bài kiểm tra: 28 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu!!

00:00:00

Câu 1: Thông hiểu
Chọn đáp án đúng
Nhiệt độ trong 55 ngày của một địa phương được cho trong bảng ghép lớp sau:

Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất nằm trong khoảng
- A.
  $(20;21)$ .
- B.
  $(19;20)$ .
- C.
  $(23;25)$ .
- D.
  $(17;19)$ .
Hướng dẫn:
Nhiệt độ trung bình trong một ngày là:

$\overline{x} = \frac{20,5.5 + 23,5.7 + 26,5.8 + 29,5.16 + 32,5.12 + 35,5.7}{55} = 28,9$

Phương sai của mẫu số liệu là:

$S^{2} = \frac{1}{55}[20,5^{2}.5 + 23,5^{2}.7 +26,5^{2}.8$ $+ 29,5^{2}.16 + 32,5^{2}.12 + 35,5^{2}.7] - 28,9^{2} =19,44$

Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất là $S^{2} = 19,4$
Câu 2: Nhận biết
Chọn kết luận đúng
Một mẫu số liệu ghép nhóm có phương sai bằng 25 thì có độ lệch chuẩn bằng
- A.
  $256.$
- B.
  $5.$
- C.
  $50.$
- D.
  $4.$
Hướng dẫn:
Ta có độ lệch chuẩn bằng căn bậc hai số học của phương sai nên $s = 5.$
Câu 3: Thông hiểu
Xác định phương sai của mẫu số liệu
Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống như sau:

Phương sai của mẫu số liệu trên:
- A.
  $155$ .
- B.
  $154$ .
- C.
  $154,56$ .
- D.
  $150$ .
Hướng dẫn:
Chiều cao trung bình của 25 cây dừa là:

$\overline{x} = \frac{4.5 + 6.15 + 7.25 +5.35 + 3.45}{25}= 23,8$ .

Phương sai

$s^{2} = \frac{4.5^{2} + 6.15^{2} + 7.25^{2} + 5.35^{2} + 3.45^{2}}{25} - 23,8^{2} = 154,56$ .
Câu 4: Nhận biết
Chọn đáp án đúng
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng bằng 3 thì có phương sai bằng
- A.
  $s^{2} = 3.$
- B.
  $s^{2} = 6.$
- C.
  $s^{2} = \sqrt{3}.$
- D.
  $s^{2} = 9.$
Hướng dẫn:
Phương sai: $s^{2} = 9.$
Câu 5: Thông hiểu
Tính phương sai của mẫu số liệu ghép nhóm
Thống kê điểm trắc nghiệm môn Tiếng Anh của 40 học sinh, người ta có bảng sau:

Tính phương sai của mẫu số liệu ghép nhóm trên.
- A.
  404,75
- B.
  450,12
- C.
  432,13
- D.
  440,87
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Điểm trung bình là:

$\overline{x} = \frac{3 \cdot 25 + 5 \cdot 35 + 5 \cdot 45 + 8 \cdot 55 + 7 \cdot 65 + 5 \cdot 75 + 3 \cdot 85 + 4 \cdot 95}{40} = 59,5$ .

Phương sai là:

$S^{2} = \frac{1}{40}\lbrack 3 \cdot (25)^{2} + 5 \cdot (35)^{2} + 5 \cdot (45)^{2} + 8 \cdot (55)^{2} + 7 \cdot (65)^{2}$

$+ 5 \cdot (75)^{2} + 3 \cdot (85)^{2} + 4 \cdot (95)^{2}\rbrack - (59,5)^{2} = 404,75$
Câu 6: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm
Thống kê doanh thu (đơn vị: triệu đô la) của 20 công ty sản xuất ô tô trong năm 2023, người ta có bảng sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
- A.
  28,23
- B.
  24,88
- C.
  20,76
- D.
  26,02
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Điểm trung bình là:

$\overline{x} = \frac{5 \cdot 10 + 5 \cdot 30 + 6 \cdot 50 + 2 \cdot 70 + 2 \cdot 90}{20} = 41$ .

Phương sai là:

$S^{2} = \frac{1}{20}\left\lbrack 5 \cdot (10)^{2} + 5 \cdot (30)^{2} + 6 \cdot (50)^{2} + 2 \cdot (70)^{2} + 2 \cdot (90)^{2} \right\rbrack - (41)^{2} = 619$ .

Độ lệch chuẩn: $S = \sqrt{619} \approx 24,88$ .
Câu 7: Thông hiểu
Tính độ lệch chuẩn của mẫu số liệu
Đo chiều cao (tính bằng $cm$ ) của $500$ học sinh trong một trường THPT ta thu được kết quả như sau:

Độ lệch chuẩn của mẫu số liệu trên là
- A.
  $s_{x} = 8,2$
- B.
  $s_{x}^{} = 161,4$
- C.
  $s_{x} = 3,85$
- D.
  $s_{x}^{} = 14,48$ .
Hướng dẫn:
Ta có bảng sau

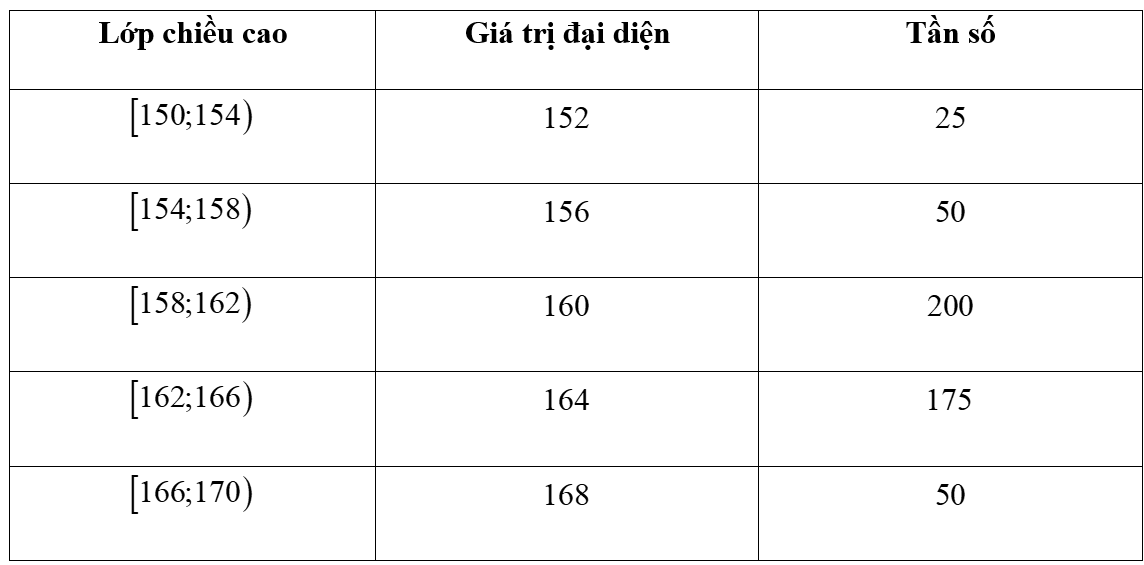
Ta có chiều cao trung bình:

$\overline{x} = \frac{1}{500}(152.25 + 156.50 + 160.200 + 164.175 + 168.50) = 161,4$

Phương sai của mẫu số liệu:

$s_{x}^{2} = f_{1}\left( c_{1} - \overline{x} \right)^{2} + f_{2}\left( c_{2} - \overline{x} \right)^{2} + ... + f_{k}\left( c_{k} - \overline{x} \right)^{2}$

$= \frac{1}{500}\lbrack 25(152 - 161,4)^{2} + 50(156 - 161,4)^{2} + 200(160 - 161,4)^{2}$

$+ 175(164 - 161,4)^{2} + 50(168 - 161,4)^{2}\rbrack = 14,84$

=> Độ lệch chuẩn: $s_{x} = \sqrt{s_{x}^{2}} = \sqrt{14,48} = 3,85$
Câu 8: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm
Khảo sát chiều cao (đơn vị $cm$ ) của học sinh lớp 12A, ta thu được kết quả như sau:

Kết quả đo ( $cm$ )
$\lbrack 150;155)$ $\lbrack 155;160)$ $\lbrack 160;165)$ $\lbrack 165;170)$ $\lbrack 170;175)$

Số học sinh
6
10

14

5

5

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên thuộc khoảng nào sau đây:
- A.
  $(7;7,5)$ .
- B.
  $(6;6,5)$ .
- C.
  $(6,5;7)$ .
- D.
  $(5,5;6)$ .
Hướng dẫn:
Chọn giá trị đại diện cho các nhóm số liệu, ta có:

Giá trị đại diện
$152,5$ $157,5$ $162,5$ $167,5$ $172,5$

Số học sinh
6
10

14

5

5

Tổng số học sinh tham gia khảo sát là : $n = 6 + 10 + 14 + 5 + 5 = 40$ .

Chiều cao trung bình của học sinh trong lớp là:

$\overline{x} = \frac{152,5.6 + 157,5.10 +162,5.14 + 167,5.5 + 172,5.5}{40}$ $= 161,625 \approx 161,6$ .

Phương sai của mẫu số liệu trên là :

$s^{2} = \frac{m_{1}\left( x_{1} - \overline{x} \right)^{2} + \ldots + m_{k}\left( x_{k} - \overline{x} \right)^{2}}{n}$

$= \frac{1}{40}\lbrack 6(152,5 - 161,6)^{2} + 10(157,5 - 161,6)^{2} + 14(162,5 - 161,6)^{2}$

$+ 5(167,5 - 161,6)^{2} + 6(172,5 - 161,6)^{2}\rbrack \approx 36,1$

Độ lệch chuẩn của mẫu số liệu trên là $s = \sqrt{s^{2}} = \sqrt{36,1} \approx 6,009$ .
Câu 9: Thông hiểu
Tìm phương sai của mẫu số liệu
Cho mẫu số liệu ghép nhóm thống kê cân nặng của học sinh lớp 12A như sau:

Nhóm số liệu
$\lbrack 40;45)$ $\lbrack 45;50)$ $\lbrack 50;55)$ $\lbrack 55;60)$ $\lbrack 60;65)$

Số học sinh

3

12

9

7

9

Phương sai của mẫu số liệu ghép nhóm là:
- A.
  $\sqrt{41,11}$ .
- B.
  $41,11$ .
- C.
  $41,45$ .
- D.
  $\sqrt{40,11}$ .
Hướng dẫn:
Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:

$\overline{x} = \frac{3.42,5 + 12.47,5 + 9.52,5 + 7.57,5 + 9.62,5}{40} = 53,375$ .

Phương sai:

$s^{2} = \frac{3.42,5^{2} + 12.47,5^{2} +9.52,5^{2} + 7.57,5^{2} + 9.62,5^{2}}{40}$ $- (53,375)^{2} \approx41,11$
Câu 10: Nhận biết
Chọn kết luận đúng
Nếu thay đổi tất cả các tần số trong mẫu số liệu ghép nhóm trên bằng 4 thì số đặc trưng nào sau đây không thay đổi?
- A.
  Phương sai
- B.
  Độ lệch chuẩn
- C.
  Khoảng tứ phân vị
- D.
  Khoảng biến thiên
Hướng dẫn:
Theo công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: $R = a_{k + 1}- a_{1}$ ta thấy khoảng biến thiên không phụ thuộc vào các tần số trong mẫu số liệu ghép nhóm nên khoảng biến thiên sẽ không thay đổi khi tần số thay đổi.
Câu 11: Thông hiểu
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được thống kê ở bảng sau:

Thời gian sử dụng
$\lbrack 7,2;7,4)$ $\lbrack 7,4;7,6)$ $\lbrack 7,6;7,8)$ $\lbrack 7,8;8,0)$

Số máy

2

4

7

6

Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?
- A.
  $0,193$ .
- B.
  $0,037$
- C.
  $0,2$
- D.
  $0,192$ .
Hướng dẫn:
Từ bảng thống kê ta có:

Thời gian sử dụng
$\lbrack 7,2;7,4)$ $\lbrack 7,4;7,6)$ $\lbrack 7,6;7,8)$ $\lbrack 7,8;8,0)$

Giá trị đại diện

7,3

7,5

7,7

7,9

Số máy

2

4

7

6

Tổng số máy: $n = 2 + 4 + 7 + 6 = 19$ .

Thời gian sử dụng trung bình của pin là:

$\overline{x} = \frac{2.7,3 + 4.7,5 + 7.7,7 + 6.7,9}{19} = \frac{1459}{190}$

Phương sai của mẫu số liệu là:

$S^{2} = \frac{1}{19}\left( 2.7,3^{2} + 4.7,5^{2} + 7.7,7^{2} + 6.7,9^{2} \right) - \left( \frac{1459}{190} \right)^{2} \approx 0,037$ .

Độ lệch chuẩn của mẫu số liệu là: $S = \sqrt{S^{2}} \approx \sqrt{0,037} \approx 0,192$ .
Câu 12: Thông hiểu
Chọn đáp án đúng
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

Quãng đường (km)

[2,7; 3,0)

[3,0; 3,3)

[3,3; 3,6)

[3,6; 3,9)

[3,9; 4,2)

Số ngày

3

6

5

4

2

Biết phương sai của mẫu số liệu được tính theo công thức:

$S^{2} = \frac{1}{n}\left\lbrack m_{1}x_{1}^{2} + m_{2}x_{2}^{2} + ... + m_{k}x_{k}^{2} \right\rbrack - {\overline{x}}^{2}.$ Khi đó giá trị của phương sai là
- A.
  11,62.
- B.
  3,39.
- C.
  0,36.
- D.
  0,1314.
Hướng dẫn:
Ta có bảng sau:

Quãng đường (km)

[2,7; 3,0)

[3,0; 3,3)

[3,3; 3,6)

[3,6; 3,9)

[3,9; 4,2)

Giá trị đại diện

2,85

3,15

3,45

3,75

4,05

Số ngày

3

6

5

4

2

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x} = \frac{3.2,85 + 6.3,15 + 5.3,45 + 4.3,75 + 2.4,05}{20} = 3,39$

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{20}\lbrack 3.(2,85)^{2} + 6.(3,15)^{2} + 5.(3,45)^{2}$

$+ 4.(3,75)^{2} + 2.(4,05)^{2}\rbrack - (3,39)^{2} = 0,1314$

Câu 13: Vận dụng

Chọn đáp án chính xác

Thời gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 hai trường X và Y được ghi lại ở bảng sau. Gọi độ lệch chuẩn thời gian gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 ở trường X và Y lần lượt là $S_{X}$ và $S_{Y}$ . Tính $S_{X} - S_{Y}$ bằng bao nhiêu?

Thời gian (Phút)	$\lbrack 6;7)$	$\lbrack 7;8)$	$\lbrack 8;9)$	$\lbrack 9;10)$	$\lbrack 10;11)$
Số học sinh trường X	8	10	13	10	9
Số học sinh trường Y	4	12	17	14	3

A.
0,49
B.
0,53
C.
0,34
D.
0,29

Hướng dẫn:

Ta lập bảng theo giá trị đại diện như sau:

Thời gian (Phút)	$\lbrack 6;7)$	$\lbrack 7;8)$	$\lbrack 8;9)$	$\lbrack 9;10)$	$\lbrack 10;11)$
Giá trị đại diện	6,5	7,5	8,5	9,5	10,5
Số học sinh trường X	8	10	13	10	9
Số học sinh trường Y	4	12	17	14	3

Cỡ mẫu $n_{X} = 8 + 10 + 13 + 10 + 9 = 50,\ \ n_{Y} = 4 + 12 + 17 + 14 + 3 = 50$ .

Thời gian trung bình hoàn thành một bài viết chính tả của học sinh trường $X$ là:

${\overline{x}}_{X} = \frac{8 \cdot 6,5 + 10 \cdot 7,5 + 13 \cdot 8,5 + 10 \cdot 9,5 + 9 \cdot 10,5}{50} = 8,54$

Phương sai của mẫu số liệu ghép nhóm của trường X là:

$S_{X}^{2} = \frac{1}{50}[ 8\cdot (6,5)^{2} + 10 \cdot (7,5)^{2}$ $+ 13 \cdot (8,5)^{2} + 10 \cdot(9,5)^{2} + 9 \cdot (10,5)^{2}] - (8,54)^{2} =1,76$

Độ lệch chuẩn của mẫu số liệu ghép nhóm của trường X là:

$S_{X} = \sqrt{S_{X}^{2}} = \sqrt{1,76} \approx 1,33$

Thời gian trung bình hoàn thành một bài viết chính tả của học sinh trường Y là:

${\overline{x}}_{Y} = \frac{4 \cdot 6,5 + 12 \cdot 7,5 + 17 \cdot 8,5 + 14 \cdot 9,5 + 3 \cdot 10,5}{50} = 8,5$

Phương sai của mẫu số liệu ghép nhóm của trường Y là:

$S_{Y}^{2} = \frac{1}{50}[ 4\cdot (6,5)^{2} + 12 \cdot (7,5)^{2} + 17 \cdot (8,5)^{2}$ $+ 14 \cdot(9,5)^{2} + 3 \cdot (10,5)^{2} ] - (8,5)^{2} =1,08$

Độ lệch chuẩn của mẫu số liệu ghép nhóm của trường Y là:

$S_{Y} = \sqrt{S_{Y}^{2}} = \sqrt{1,08} \approx 1,04$

Vậy $S_{X} - S_{Y} = 1,33 - 1,04 = 0,29$

Câu 14: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm
Điều tra về số tiền mua sách (đơn vị: nghìn đồng) trong một năm của 50 học sinh trong một trường THPT, người ta có bảng sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
- A.
  265,34
- B.
  264,12
- C.
  233,98
- D.
  242,29
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Điểm trung bình là:

$\overline{x} = \frac{29 \cdot 100 + 11 \cdot 300 + 3 \cdot 500 + 4 \cdot 700 + 3 \cdot 900}{50} = 264$ .

Phương sai là:

$S^{2} = \frac{1}{50}\lbrack 29 \cdot (100)^{2} + 11 \cdot (300)^{2} + 3 \cdot (500)^{2}$ $+ 4 \cdot (700)^{2} + 3 \cdot (900)^{2}\rbrack - (264)^{2} = 58704$ .

Độ lệch chuẩn: $S = \sqrt{58704} \approx 242,29$ .
Câu 15: Thông hiểu
Tính phương sai của mẫu số liệu
Cho bảng phân bố tần số ghép lớp về độ dài của 60 lá dương xỉ trưởng thành như sau:

Độ dài (cm)
$\lbrack 10;20)$ $\lbrack 20;30)$ $\lbrack 30;40)$ $\lbrack 40;50\rbrack$

Tần số
8 18 24 10

Tính phương sai bảng phân bố tần số ghép lớp đã cho
- A.
  $\mathbf{s}_{\mathbf{x}}^{\mathbf{2}}\mathbf{=}\mathbf{86}$ .
- B.
  $\mathbf{s}_{\mathbf{x}}^{\mathbf{2}}\mathbf{=}\mathbf{83}$ .
- C.
  $\mathbf{s}_{\mathbf{x}}^{\mathbf{2}}\mathbf{=}\mathbf{85}$ .
- D.
  $\mathbf{s}_{\mathbf{x}}^{\mathbf{2}}\mathbf{=}\mathbf{84}$ .
Hướng dẫn:

Độ dài (cm)
$\lbrack 10;20)$ $\lbrack 20;30)$ $\lbrack 30;40)$ $\lbrack 40;50\rbrack$

Giá trị đại diện
$15$ $25$ $35$ $45$

Tần số
8 18 24 10

Trước hết ta có $\overline{x} = \frac{15.8 + 25.18 + 35.24 + 45.10}{60} = 31$ .

Khi đó phương sai:

$s_{x}^{2} = \frac{8.(15 - 31)^{2} + 18 \cdot (25 - 31)^{2} + 24.(35 - 31)^{2} + 10.(45 - 31)^{2}}{60} = 84$
Câu 16: Thông hiểu
Tính phương sai của mẫu số liệu ghép nhóm
Khảo sát thời gian chơi thể thao trong một ngày của 42 học sinh được cho trong bảng sau (thời gian đơn vị phút):

Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất là
- A.
  $597$ .
- B.
  $2477,1$ .
- C.
  $598$
- D.
  $256,2$ .
Hướng dẫn:
Trung bình thời gian chơi thể thao trong một ngày của một học sinh là:

$\overline{x} = \frac{10.5 + 30.9 + 50.12 + 70.10 + 90.6}{42} = \frac{360}{7} = 51,42857143$

Phương sai của mẫu số liệu là:

$S^{2} = \frac{5.10^{2} + 9.30^{2} + 12.50^{2} + 10.70^{2} + 6.90^{2}}{42} - \left( \frac{360}{7} \right)^{2}$

$= \frac{29300}{49} = 597,9591837 \approx 598$

Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất là $S^{2} \approx 598$
Câu 17: Thông hiểu
Tính phương sai của mẫu số liệu ghép nhóm
Điều tra 42 học sinh của một lớp 12 về số giờ tự học ở nhà, người ta có bảng thống kê sau:

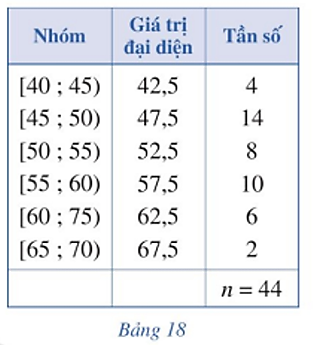
Tính phương sai của mẫu số liệu ghép nhóm trên.
- A.
  1,276
- B.
  1,538
- C.
  1,302
- D.
  1,431
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Số giờ học trung bình là:

$\overline{x} = \frac{8 \cdot 1,5 + 10\cdot 2,5 + 12 \cdot 3,5 + 9 \cdot 4,5 + 3 \cdot 5,5}{42}$ $=\frac{68}{21} \approx 3,238$ .

Phương sai là:

$S^{2} = \frac{1}{42}[8 \cdot(1,5)^{2} + 10 \cdot (2,5)^{2} + 12 \cdot (3,5)^{2} + 9 \cdot (4,5)^{2}$ $+ 3 \cdot (5,5)^{2} ]- \left( \frac{68}{21} \right)^{2} =\frac{2525}{1764} \approx 1,431$ .
Câu 18: Vận dụng
Tính giá trị của biểu thức P
Một giống xoan đào được trồng tại hai địa điểm $A$ và $B$ . Người ta thống kê đường kính thân cây của một số cây xoan đào 5 tuổi ở bảng sau:

Đường kính (cm)
$\lbrack 30;\ 32)$ $\lbrack 32;\ 34)$ $\lbrack 34;\ 36)$ $\lbrack 36;\ 38)$ $\lbrack 38;\ 40)$

Số cây trồng ở điểm A

25

38

20

10

7

Số cây trồng ở điểm B

22

27

19

18

14

Gọi $a$ và $b$ là phương sai về đường kính cây trồng ở hai địa điểm $A$ và $B$ . Tính giá trị biểu thức $P = \frac{a}{b}$ (làm tròn đến hàng phần trăm).
- A.
  $P \approx 0,70$
- B.
  $P \approx 0,63$
- C.
  $P \approx 0,74$
- D.
  $P \approx 0,68$
Hướng dẫn:
Cỡ mẫu $n = 25 + 38 + 20 + 10 + 7$ $= 22 +27 + 19 + 18 + 14 = 100$

Đường kính thân cây trung bình của một số cây xoan đào trồng ở hai địa điểm $A$ và $B$ tương ứng là

$\overline{x_{A}} = \frac{1}{100}(25.31 + 38.33 + 20.35 + 10.37 + 7.39) = 33,72$

$\overline{x_{B}} = \frac{1}{100}(22.31 + 27.33 + 19.35 + 18.37 + 14.39) = 34,5$

Phương sai đường kính của cây ở hai địa điểm A, B lần lượt là

$S_{x_{A}}^{2} = \dfrac{1}{100}[ 25.(31 - 33,72)^{2} + 38.(33 -33,72)^{2}$ $+ 20.(35 - 33,72)^{2} + 10.(37 - 33,72)^{2} + 7.(39 -33,72)^{2} ] = 5,4016$

$S_{x_{B}}^{2} = \dfrac{1}{100}ơ 22.(31 - 34,5)^{2} + 27.(33 -34,5)^{2}$ $+ 19.(35 - 34,5)^{2} + 18.(37 - 34,5)^{2} + 14.(39 - 34,5)^{2}] = 7,31.$

Khi đó $P = \frac{a}{b} \approx 0,74$ .
Câu 19: Nhận biết
Chọn đáp án đúng
Cho mẫu số liệu ghép nhóm thống kê có phương sai bằng là 4. Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
- A.
  $4$ .
- B.
  $16$ .
- C.
  $2$ .
- D.
  $8$ .
Hướng dẫn:
Độ lệch chuẩn là: $s = \sqrt{4} = 2$ .
Câu 20: Vận dụng
Tìm phương sai của mẫu số liệu ghép nhóm
Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau. Hãy tính phương sai của mẫu số liệu ghép nhóm với nhóm đầu tiên là $\lbrack 42;46)$ và độ dài mỗi nhóm bằng $4$ . (làm tròn đến hàng phần mười)

42

43,4

43,4

46,5

46,7

46,8

47,5

47,7

48,1

48,4

50,8

52,1

52,7

53,9

54,8

55,6

57,5

59,6

60,3

61,1
- A.
  26,6
- B.
  28,5
- C.
  20,3
- D.
  22,7
Hướng dẫn:
Ta lập được bảng số liệu ghép nhóm theo giá trị đại diện như sau:

Tốc độ (km/h)
$\lbrack 42;46)$ $\lbrack 46;50)$ $\lbrack 50;54)$ $\lbrack 54;58)$ $\lbrack 58;62)$

Giá trị đại diện

44

48

52

56

60

Số xe

3

7

4

3

3

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x} = \frac{3 \cdot 44 + 7 \cdot 48 + 4 \cdot 52 + 3 \cdot 56 + 3 \cdot 60}{20} = 51,2$

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{20}\left( 3 \cdot 44^{2} + 7 \cdot 48^{2} + 4 \cdot 52^{2} + 3 \cdot 56^{2} + 3 \cdot 60^{2} \right) - (51,2)^{2} \approx 26,6$
Câu 21: Thông hiểu
Tìm phương sai của mẫu số liệu ghép nhóm
Phương sai của một mẫu số liệu ghép nhóm cho bởi bảng thống kê dưới đây là:
- A.
  $13,24$
- B.
  $15,74$
- C.
  $18,84$
- D.
  $14,84$
Hướng dẫn:
Ta có chiều cao trung bình:

$\overline{x} = \frac{1}{500}(152.25 + 156.50 + 160.200 + 164.175 + 168.50) = 161,4$

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{500}\lbrack 25(152 -161,4)^2 + 50(156 - 161,4)^{2}$

$+ 200(160 - 161,4)^{2} + 175(164 - 161,4)^{2} + 50(168 - 161,4)^{2}\rbrack$

$= 14,84$ .
Câu 22: Nhận biết
Chọn công thức đúng
Xét mẫu số liệu ghép nhóm cho ở bảng dưới đây. Gọi $\overline{x}$ là số trung bình cộng của mẫu số liệu ghép nhóm. Độ lệch chuẩn của mẫu số liệu ghép nhóm đó được tính bằng công thức nào trong các công thức sau?
- A.
  $s = \sqrt {\frac{{{n_1}{{\left( {{x_1} - \bar x} \right)}^2} + {n_2}{{\left( {{x_2} - \bar x} \right)}^2} + ... + {n_m}{{\left( {{x_m} - \bar x} \right)}^2}}}{m}} .$
- B.
  $s = \sqrt {\frac{{{n_1}{{\left( {{x_1} - \bar x} \right)}^2} + {n_2}{{\left( {{x_2} - \bar x} \right)}^2} + ... + {n_m}{{\left( {{x_m} - \bar x} \right)}^2}}}{n}} .$
- C.
  ${s^2} = \frac{{{n_1}{{\left( {{x_1} - \bar x} \right)}^2} + {n_2}{{\left( {{x_2} - \bar x} \right)}^2} + ... + {n_m}{{\left( {{x_m} - \bar x} \right)}^2}}}{m}.$
- D.
  ${s^2} = \frac{{{n_1}{{\left( {{x_1} - \bar x} \right)}^2} + {n_2}{{\left( {{x_2} - \bar x} \right)}^2} + ... + {n_m}{{\left( {{x_m} - \bar x} \right)}^2}}}{n}.$
Hướng dẫn:
Độ lệch chuẩn của mẫu số liệu ghép nhóm được tính bởi công thức:

$s = \sqrt {\frac{{{n_1}{{\left( {{x_1} - \bar x} \right)}^2} + {n_2}{{\left( {{x_2} - \bar x} \right)}^2} + ... + {n_m}{{\left( {{x_m} - \bar x} \right)}^2}}}{n}} .$
Câu 23: Thông hiểu
Tính phương sai của mẫu số liệu ghép nhóm
Khảo sát thời gian tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:

Thời gian
$\lbrack 0;\ 20)$ $\lbrack 20;\ 40)$ $\lbrack 40;\ 60)$ $\lbrack 60;\ 80)$ $\lbrack 80;\ 100)$

Số học sinh

5

9

12

10

6

Tìm phương sai của mẫu số liệu trên. (Kết quả làm tròn đến hàng phần chục).
- A.
  $601$
- B.
  $367$
- C.
  $598$
- D.
  $485$
Hướng dẫn:
Cỡ mẫu là $n = 5 + 9 + 12 + 10 + 6 = 42$ .

Thời gian tập thể dục trung bình của $42$ học sinh khối $12$ trên là

$\overline{x} = \frac{1}{42}(5.10 + 9.30 + 12.50 + 10.70 + 6.90) = 51,4$ .

Phương sai

$S_{x}^{2} = \frac{1}{42}\lbrack 5.(10 - 51,4)^{2} + 9.(30 - 51,4)^{2} + 12.(50 - 51,4)^{2}$

$+ 10.(70 - 51,4)^{2} + 6.(90 - 51,4)^{2}\rbrack \approx 598$
Câu 24: Nhận biết
Chọn kết luận đúng
Số đặc trưng nào không sử dụng thông tin của nhóm số liệu đầu tiên và nhóm số liệu cuối cùng?
- A.
  Khoảng biến thiên.
- B.
  Độ lệch chuẩn.
- C.
  Phương sai.
- D.
  Khoảng tứ phân vị.
Hướng dẫn:
Theo các công thức tính khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn ta thấy khoảng tứ phân vị là không sử dụng thông tin của nhóm số liệu đầu và nhóm số liệu cuối.
Câu 25: Nhận biết
Chọn phương án thích hợp
Để đo mức độ phân tán về nhiệt độ không khí trung bình các tháng của năm 2023 tại Hà Nội, đại lượng thích hợp là
- A.
  Mốt.
- B.
  Số trung bình.
- C.
  Số trung vị.
- D.
  Phương sai.
Hướng dẫn:
Đại lượng đo mức độ phân tán của mẫu số liệu là phương sai.
Câu 26: Thông hiểu
Tính phương sai của mẫu số liệu ghép nhóm
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong Bảng 18.

Phương sai của mẫu số liệu ghép nhóm trên là:
- A.
  30.
- B.
  11.
- C.
  53,2.
- D.
  46,1.
Hướng dẫn:
Số trung bình cộng của mẫu số liệu ghép nhóm là:

$\overline{x} = \frac{4.42,5 + 14.47,5 + 8.52,5 + 10.57,5 + 6.62,5 + 2.67,5}{44} = \frac{585}{11}$

Phương sai của mẫu số liệu ghép nhóm là:

$s^{2} = \frac{1}{44}\lbrack 4\left( 42,5 - \frac{585}{11} \right)^{2} + 14\left( 47,5 - \frac{585}{11} \right)^{2}$ $+ 8\left( 52,5 - \frac{585}{11} \right)^{2} + 10\left( 57,5 - \frac{585}{11} \right)^{2}$

$+6\left( 62,5 - \frac{585}{11}\right)^{2} + 2.\left( 67,5 - \frac{585}{11} \right)^{2}\rbrack \approx46,12$

Câu 27: Thông hiểu

Tìm phương sai của mẫu số liệu

Thời gian truy cập Internet mỗi buổi tối (đơn vị: phút) của một số học sinh được thống kê ở bảng sau:

Thời gian	[10,5; 12,5)	[12,5; 14,5)	[14,5; 16,5)	[16,5; 18,5)	[18,5; 20,5)
Số học sinh	3	12	15	24	2

Phương sai của mẫu số liệu trên là:

A.
$s^{2} \approx 3,87$ .
B.
$s^{2} \approx 1,87$ .
C.
$s^{2} \approx 4,87$ .
D.
$s^{2} \approx 2,87$ .

Hướng dẫn:

Ta viết lại bảng ở đề bài như sau:

Thời gian	[10,5; 12,5)	[12,5; 14,5)	[14,5; 16,5)	[16,5; 18,5)	[18,5; 20,5)
Giá trị đại diện	11,5	13,5	15,5	17,5	19,5
Số học sinh	3	12	15	24	2	$n = 56$

Số trung bình cộng của mẫu số liệu ghép nhóm biểu thị số phút truy cập internet mỗi buổi tối của một số học sinh là:

$\overline{x} = \frac{3.11,5 + 12.13,5 + 15.15,5 + 24.17,5 + 2.19,5}{56} \approx 15,86$ (phút)

Vậy phương sai của mẫu số liệu ghép nhóm biểu thị số phút truy cập internet mỗi buổi tối của một số học sinh là:

$s^{2} = \frac{1}{56}\lbrack 3.(11,5 - 15,86)^{2} + 12.(13,5 - 15,86)^{2} + 15.(15,5 - 15,86)^{2}$

$+ 24.(17,5 - 15,86)^{2} + 2.(19,5 - 15,86)^{2}\rbrack \approx 3,87$

Câu 28: Vận dụng

Tính giá trị của biểu thức

Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau. Gọi phương sai đường kính thân của một số cây xoan đào 5 năm tuổi ở địa điểm A và địa điểm B lần lượt là $S_{A}^{2}$ và $S_{B}^{2}$ . Tính $T = \left| S_{A}^{2} - S_{B}^{2} \right|$ bằng bao nhiêu?

Đường kính (cm)	$\lbrack 30;32)$	$\lbrack 32;34)$	$\lbrack 34;36)$	$\lbrack 36;38)$	$\lbrack 38;40)$
Số cây trồng ở địa điểm A	25	38	20	10	9
Số cây trồng ở địa điểm B	22	27	19	14	14

A.
$T = 1,81$
B.
$T = 1, 72$
C.
$T = 1,91$
D. $T = 1,63$

Hướng dẫn:

Ta lập bảng theo giá trị đại diện như sau:

Đường kính (cm)	$\lbrack 30;32)$	$\lbrack 32;34)$	$\lbrack 34;36)$	$\lbrack 36;38)$	$\lbrack 38;40)$
Giá trị đại diện	31	33	35	37	39
Số cây trồng ở địa điểm A	25	38	20	10	9
Số cây trồng ở địa điểm B	22	27	19	14	14

Cỡ mẫu: $n_{A} = 25 + 38 + 20 + 10 + 7 = 100;$ $n_{B} = 22 + 27 + 19 + 18 + 14 = 100$

Đường kính trung bình của thân cây xoan đào trồng tại địa điểm A là:

${\overline{x}}_{A} = \frac{25 \cdot 31 + 38 \cdot 33 + 20 \cdot 35 + 10 \cdot 37 + 7 \cdot 39}{100} = 33,72$

Phương sai của mẫu số liệu ghép nhóm vè̀ đường kính của thân cây xoan đào trồng tại địa điểm A là:

$S_{A}^{2} = \frac{1}{100}\left( 25 \cdot 31^{2} + 38 \cdot 33^{2} + 20 \cdot 35^{2} + 10 \cdot 37^{2} + 7 \cdot 39^{2} \right) - (33,72)^{2} \approx 5,40$

Đường kính trung bình của thân cây xoan đào trồng tại địa điểm B là:

${\overline{x}}_{B} = \frac{22 \cdot 31 + 27 \cdot 33 + 19 \cdot 35 + 18 \cdot 37 + 14 \cdot 39}{100} = 34,5$

Phương sai của mẫu số liệu ghép nhóm về đường kính của thân cây xoan đào trồng tại địa điểm B là:

$S_{B}^{2} = \frac{1}{100}\left( 22 \cdot 31^{2} + 27 \cdot 33^{2} + 19 \cdot 35^{2} + 18 \cdot 37^{2} + 14 \cdot 39^{2} \right) - (34,5)^{2} = 7,31$

Vậy $\left| S_{A}^{2} - S_{B}^{2} \right| = |5,40 - 7,31| = 1,91$

0/28

28 câu:

Kiểm tra Kiểm tra lại Tiếp tục Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:

Nhận biết (25%):

2/3
Thông hiểu (61%):

2/3
Vận dụng (14%):

2/3

Thời gian làm bài: 00:00:00
Số câu làm đúng: 0
Số câu làm sai: 0
Điểm số: 0
Điểm thưởng: 0

Làm lại

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay

Chia sẻ bởi:
Su kem

23 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

A. CHUYÊN ĐỀ TRỌNG TÂM
B. CHUYÊN ĐỀ TRẮC NGHIỆM

Kết quả đo ( $cm$ )	$\lbrack 150;155)$	$\lbrack 155;160)$	$\lbrack 160;165)$	$\lbrack 165;170)$	$\lbrack 170;175)$
Số học sinh	6	10	14	5	5

Quãng đường (km)	[2,7; 3,0)	[3,0; 3,3)	[3,3; 3,6)	[3,6; 3,9)	[3,9; 4,2)
Số ngày	3	6	5	4	2

Quãng đường (km)	[2,7; 3,0)	[3,0; 3,3)	[3,3; 3,6)	[3,6; 3,9)	[3,9; 4,2)
Giá trị đại diện	2,85	3,15	3,45	3,75	4,05
Số ngày	3	6	5	4	2

Độ dài (cm)	$\lbrack 10;20)$	$\lbrack 20;30)$	$\lbrack 30;40)$	$\lbrack 40;50\rbrack$
Tần số	8	18	24	10

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bài tập Tính phương sai và độ lệch chuẩn Có đáp án (Tiếp)

Trắc nghiệm Toán 12: Phương sai và độ lệch chuẩn - Có hướng dẫn chi tiết

Chúc mừng Bạn đã hoàn thành bài!

A. CHUYÊN ĐỀ TRỌNG TÂM

B. CHUYÊN ĐỀ TRẮC NGHIỆM

Lớp 12

Toán 12

Chuyên đề Toán 12

Chuyên đề Toán 12

Tìm m để tiếp tuyến tại M song song với đường thẳng cho trước

Tìm m để phương trình có nghiệm thuộc khoảng, đoạn

Cách tìm điều kiện của m để phương trình có nghiệm Toán 12

Tìm tham số m để đồ thị hàm số cắt trục hoành tại một điểm duy nhất

Tìm tiệm cận ngang của đồ thị hàm số

Cách tìm tiệm cận đứng của đồ thị hàm số nhanh và chính xác