Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập Xác suất toàn phần Công thức Bayes mức độ Thông Hiểu

Chuyên đề Xác suất có điều kiện Toán 12

Chuyên đề xác suất công thức Bayes toán 12

Hy vọng qua các bài tập xác suất toàn phần và công thức Bayes mức độ thông hiểu trong bài viết, bạn đã nắm vững các phương pháp suy luận, phân tích tình huống và vận dụng linh hoạt công thức vào bài toán thực tế. Đây là nền tảng quan trọng giúp bạn tự tin bước vào các câu hỏi vận dụng và vận dụng cao trong kỳ thi THPT Quốc gia. Đừng quên luyện tập thường xuyên và kết hợp với các chuyên đề Toán lớp 12 khác như tổ hợp – xác suất, biến cố, quy tắc cộng – nhân… để đạt kết quả cao nhất trong kỳ thi. Hãy lưu lại bài viết và chia sẻ đến bạn bè để cùng nhau học tốt môn Toán nhé!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 27 câu
  • Điểm số bài kiểm tra: 27 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Tính xác xuất của biến cố

    Một hộp chứa bóng xanh và bóng đỏ. Biết rằng xác suất của việc chọn được một quả bóng xanh là 0.6. Xác suất chọn được một quả bóng xanh biết rằng quả bóng đó là bị lỗi là 0.7. Xác suất chọn được một quả bóng bị lỗi là 0.2. Xác suất chọn bóng bị lỗi biết bóng đã chọn màu xanh là bao nhiêu?

    Hướng dẫn:

    Gọi biến cố X:''Chọn được quả bóng xanh'', biến cố L:''chọn được quả bóng lỗi''.

    Ta có:

    P(X) = 0.6 : xác suất chọn được bóng xanh.

    P(X|L) = 0.7: xác suất chọn được bóng xanh biết bóng bị lỗi.

    P(L) = 0.2: xác suất chọn được bóng bị lỗi.

    Xác suất chọn bóng bị lỗi biết bóng đã chọn màu xanh là:

    P(L|X) = P\left( X|L \right).\frac{P(L)}{P(X)} = 0.7.\frac{0.2}{0.6} = \frac{7}{30}

  • Câu 2: Thông hiểu
    Tính xác suất của biến cố A

    Cho A, B là hai biến cố. Biết P(B) = 0,2. Nếu B không xảy ra thì thỉ lệ A xảy ra là 2\%. Nếu B xảy ra thì tỉ lệ A xảy ra 4\%. Xác suất của biến cố A là bao nhiêu?

    Hướng dẫn:

    Ta có:

    P(B) = 0,2 \Rightarrow P(\overline{B}) = 0,8.

    Vì B xảy ra thì tỉ lệ A sảy ra 4\% nên P(A|B) = 0,04.

    Tương tự ta cũng có P(A|\overline{B}) = 0,02.

    Theo công thức xác suất toàn phần ta có:

    P(A) = P(B).P(A|B) + P(\overline{B}).P(A|\overline{B})

    = 0,2.0,04 + 0,8.0,0 2 = 0,024.

  • Câu 3: Thông hiểu
    Tính xác suất để tổng số chấm bằng 6

    Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6 biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm. (Làm tròn đến hàng phần trăm).

    Hướng dẫn:

    Gọi A là biến cố “con xúc xắc thứ nhất xuất hiện mặt 4 chấm”

    Gọi B là biến cố “Tổng số chấm xuất hiện trên 2 con xúc xắc bằng 6”.

    Khi con xúc xắc thứ nhất đã xuất hiện mặt 4 chấm thì thì lần thứ hai xuất hiện 2 chấm thì tổng hai lần xuất hiện là 6 chấm thì P\left( B|A \right) = \frac{1}{6} \approx 0,17

  • Câu 4: Thông hiểu
    Chọn đáp án đúng

    Cho bảng dữ liệu sau về kết quả xét nghiệm một loại bệnh:

    Dương tính

    Âm tính

    Mắc bệnh

    100

    20

    Không mắc bệnh

    30

    850

    Nếu một người có kết quả xét nghiệm dương tính, xác suất người đó mắc bệnh là bao nhiêu?

    Hướng dẫn:

    Gọi biến cố A: "Người đó mắc bệnh"

    Biến cố B:''Người đó có kết quả xét nghiệm dương tính''.

    Với P\left( B|A \right): xác suất kết quả dương tính khi người đó mắc bệnh

    P\left( B|A \right) = \frac{100}{100 + 20} = \frac{5}{6}.

    \begin{matrix}P(A) = \dfrac{100 + 20}{1000} = \dfrac{120}{1000} = 0.12.\end{matrix}

    P(B) = \frac{100 + 30}{1000} = 0.13

    Từ đó suy ra: P\left( A|B \right) = \frac{P\left( B|A \right).P(A)}{P(B)} = \frac{5}{6}.\frac{0.12}{0.13} = 0.7692 \simeq 77\%.

  • Câu 5: Thông hiểu
    Tính P(A|B)

    Cho hai biến cố A và B, với P(A) = 0,2, P\left( B|A \right) = 0,7, P\left( B|\overline{A} \right) = 0,15. Tính P\left( A|B \right).

    Hướng dẫn:

    Ta có: P(A) = 0,2 \Rightarrow P\left( \overline{A} \right) = 0,8, P\left( B|A \right) = 0,7, P\left( B|\overline{A} \right) = 0,15.

    P(B) = P(A).P\left( B|A \right) + P\left( \overline{A} \right).P\left( B|\overline{A} \right) 

    \Rightarrow P(B) = 0,2.0,7 + 0,8.0,15 = 0,26.

    Theo công thức Bayes:

    P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(B)} \Rightarrow P\left( A|B \right) = \frac{0,2.0,7}{0,26} = \frac{7}{13}.

  • Câu 6: Thông hiểu
    Chọn đáp án chính xác

    Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là bao nhiêu? (Làm tròn đến hàng phần trăm).

    Hướng dẫn:

    A: "học sinh đã làm đúng bài toán đầu tiên"

    \Rightarrow P(A) = 60\% = 0,6.

    B: "học sinh đã làm đúng bài toán thứ hai"

    \Rightarrow P(B) = 40\% = 0,4.

    A \cap B: "học sinh làm đúng cả hai bài toán"

    \Rightarrow P(A \cap B) = 20\% = 0,2.

    Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là

    P\left( B|A \right) = \frac{P(A \cap B)}{P(A)} = \frac{0,2}{0,6} = \frac{1}{3} \approx 0.33.

  • Câu 7: Thông hiểu
    Chọn đáp án đúng

    Trong một trường học, tỉ lệ học sinh nữ là 52\%. Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là 18\% và 15\%. Chọn ngẫu nhiên một học sinh của trường. Tính xác suất học sinh được chọn có tham gia câu lạc bộ nghệ thuật.

    Hướng dẫn:

    Gọi A là biến cố “học sinh được chọn là học sinh nữ “ và B là biến cố “Học sinh được chọn tham gia câu lạc bộ nghệ thuật”

    Khi đó ta có P(A) = 0,52, P\left( B|A \right) = 0, 18, P\left( B|\overline{A} \right) = 0,15

    Suy ra P\left( \overline{A} \right) = 1 - P(A) = 0,48.

    Áp dụng công thức xác suất toàn phần ta có

    P(B) = P(A)P\left( B|A \right) + P\left( \overline{A} \right)P\left( B|\overline{A} \right)

    = 0,52.0,18 + 0,48.0,15 = 0,1656.

  • Câu 8: Thông hiểu
    Tính giá trị của D

    Cho hai biến cố A,B thỏa mãn P(A) = 0,21;\ \ P(B) = 0,52;\ P\left( B|A\right) = 0,6. Khi đó P\left( A|B \right) = \frac{a}{b} với a,b \in \mathbb{N}^{*},\ \ \frac{a}{b} là phân số tối giản, giá trị của D = a + b là bao nhiêu?

    Hướng dẫn:

    Ta có: P(AB) = P(A).P\left( B|A \right) = 0,21.0,6 = 0,126.

    P(AB) = P(B).P\left( A|B \right)

    \Rightarrow P\left( A|B \right) = \frac{P(AB)}{P(B)} = \frac{0,126}{0,52} = \frac{63}{260}.

    Suy ra: a = 63 và b = 260.

    Vậy D = a + b = 63 + 260 = 323.

  • Câu 9: Thông hiểu
    Chọn đáp án thích hợp

    Kết quả khảo sát tại một xã cho thấy có 25\% cư dân hút thuốc lá. Tỉ lệ cư dân thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp trong số những người hút thuốc lá và không hút thuốc lá lần lượt là 60\% và 25\%, được biểu diễn ở sơ đồ hình cây sau:

    A diagram of a flowchartDescription automatically generated

    Nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp thì xác suất người đó có hút thuốc lá là bao nhiêu?

    Hướng dẫn:

    Giả sử ta gặp một cư dân của xã, gọi A là biến cố "Người đó có hút thuốc lá" và B là biến cố "Người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp". Ta có sơ đồ hình cây sau:

    Ảnh có chứa văn bản, ảnh chụp màn hình, Phông chữ, biểu đồMô tả được tạo tự động

    Ta có P(B) = P(A) \cdot P(B \mid A) +P(\overline{A}) \cdot P(B \mid \overline{A})= 0,15 + 0,1875 =0,3375.

    Theo công thức Bayes, ta có P(A \mid B) = \frac{P(A)P(B \mid A)}{P(B)} = \frac{0,15}{0,3375} = \frac{4}{9}.

  • Câu 10: Thông hiểu
    Chọn kết quả thích hợp

    Cho hai biến cố A và B có \ P(A) = 0,2;\ P(B) = 0,6;P\left( A|B \right) = 0,3. Tính \ P\left( \overline{A}B \right).

    Hướng dẫn:

    Theo công thức tính xác suất có điều kiện ta có:

    \ P\left( A|B \right) = \frac{P(AB)}{P(B)}

    \Rightarrow P(AB) = P\left( A|B \right).P(B) = 0,3.0,6 = 0,18.

    Vì \ \overline{A}B và \ AB là hai biến cố xung khắc và \ \overline{A}B \cup AB = B nên theo tính chất của xác suất, ta có:

    \ P\left( \overline{A}B \right) + P(AB) = P(B)

    \Rightarrow P\left( \overline{A}B \right) = P(B) - P(AB) = 0,6 - 0,18 = 0,42.

  • Câu 11: Thông hiểu
    Chọn phương án thích hợp

    Kết quả khảo sát tại một xã cho thấy có 25\% cư dân hút thuốc lá. Tỉ lệ cư dân thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp trong số những người hút thuốc lá và không hút thuốc lá lần lượt là 60\% và 25\%. Nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp thì xác suất người đó có hút thuốc lá là bao nhiêu?

    Hướng dẫn:

    Giả sử ta gặp một cư dân của xã, gọi A là biến cố "Người đó có hút thuốc lá" và B là biến cố "Người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp". Ta có sơ đồ hình cây sau:

    Ảnh có chứa văn bản, ảnh chụp màn hình, Phông chữ, biểu đồMô tả được tạo tự động

    Ta có

    P(B) = P(A) \cdot P(B \mid A) +P(\overline{A}) \cdot P(B \mid \overline{A})= 0,15 + 0,1875 =0,3375.

    Theo công thức Bayes, ta có:

    P(A \mid B) = \frac{P(A)P(B \mid A)}{P(B)} = \frac{0,15}{0,3375} = \frac{4}{9}.

    Vậy nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp thì xác suất người đó có hút thuốc lá là \frac{4}{9}.

  • Câu 12: Thông hiểu
    Tính xác suất để viên bi được chọn màu đỏ

    Có hai chiếc hộp đựng 50 viên bi có kích thước và khối lượng như nhau. Sau khi thống kê nhận được bảng số liệu sau:

    Chọn ngẫu nhiên một hộp, sau đó lấy ra ngẫu nhiên một viên bi từ hộp được chọn. Xác suất để chọn được viên bi màu đỏ là

    Hướng dẫn:

    Xét hai biến cố

    A: “Chọn được hộp I”;

    B: “Chọn được viên bi màu đỏ”

    P(A) = \frac{1}{2} ; P\left( \overline{A} \right) = \frac{1}{2} ; P\left( B|A \right) = \frac{20}{35} = \frac{4}{7} ; P\left( B|\overline{A} \right) = \frac{5}{15} = \frac{1}{3}.

    Áp dụng công thức xác suất toàn phần, ta có

    P(B) = P(A)P\left( B|A \right) + P\left(\overline{A} \right)P\left( B|\overline{A} \right)

    =\frac{1}{2}.\frac{4}{7} + \frac{1}{2}.\frac{1}{3} =\frac{19}{42}.

  • Câu 13: Thông hiểu
    Tính P(A)

    Cho hai biến cố A và B, với P(B) = 0,8, P\left( A|B \right) = 0,7, P\left( A|\overline{B} \right) = 0,45. Tính P(A)

    Hướng dẫn:

    Do P\left( \overline{B} \right) = 1 - P(B) = 1 - 0,8 = 0,2

    Theo công thức xác suất toàn phần ta có:

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)= 0,8.0,7 + 0,2.0,45 = 0,65

  • Câu 14: Thông hiểu
    Tính P(A|B)

    Cho P(A) = 0,35; P\left( B|A \right) = 0,4 và P\left( B|\overline{A} \right) = 0,3. Giá trị của P\left( A|B \right) là

    Hướng dẫn:

    Vì P(A) = 0,35 nên P\left( \overline{A} \right) = 1 - 0,35 = 0,65.

    Theo công thức Bayes ta có:

    P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(A).P\left( B|A \right) + P\left( \overline{A} \right).P\left( B|\overline{A} \right)}= \frac{0,35.0,4}{0,35.0,4 + 0,65.0,3} = \frac{28}{67}.

  • Câu 15: Thông hiểu
    Tính P(B)

    Cho P(A) = 0,4; P\left( B|A \right) = 0,2 và P\left( B|\overline{A} \right) = 0,3. Giá trị của P(B) là:

    Hướng dẫn:

    Vì P(A) = 0,4 nên P\left( \overline{A} \right) = 1 - 0,4 = 0,6.

    Theo công thức xác suất toàn phần ta có:

    P(B) = P(A).P\left( B|A \right) + P\left(\overline{A} \right).P\left( B|\overline{A} \right)

    = 0,4.0,2 + 0,6.0,3= 0,26.

  • Câu 16: Thông hiểu
    Chọn đáp án thích hợp

    Hàng ngày, Hùng luyện tập hai môn thể thao là bóng chuyền hoặc cầu lông. Nếu hôm nay Hùng chơi bóng chuyền thì xác suất để hôm sau Hùng chơi cầu lông là 0,6. Nếu hôm nay Hùng chơi cầu lông thì xác suất để hôm sau Hùng chơi bóng chuyền là 0,5. Xét một tuần mà thứ hai Hùng chơi bóng chuyền. Gọi hai biến cố:

    A: “Thứ ba Hùng chơi cầu lông”;

    B: “Thứ ba Hùng chơi cầu lông”

    Ta có sơ đồ hình cây biểu thị tình huống trên trong hai ngày thứ ba, thứ tư như sau:

    Xác suất bạn Hùng chơi cầu lông vào thứ tư là

    Hướng dẫn:

    Dựa theo sơ đồ hình cây, ta có

    P(B) = P(A).P\left( B|A \right) + P\left(\overline{A} \right)P\left( B|\overline{A} \right)= 0,6.0,5 + 0,4.0,6 =0,54.

  • Câu 17: Thông hiểu
    Tính xác suất để chọn được phế phẩm

    Hai máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất 35\%, máy II sản xuất 65\% tổng sản lượng. Tỉ lệ phế phẩm của các máy lần lượt là 0,3\% và 0,7\%. Chọn ngẫu nhiên 1 sản phẩm từ kho. Tính xác suất để chọn được phế phẩm?

    Hướng dẫn:

    Gọi A_{1}là biến cố “Sản phẩm được chọn do máy I sản xuất”

    A_{2} là biến cố “Sản phẩm được chọn do máy II sản xuất”

    B là biến cố “Sản phẩm được chọn là phế phẩm”

    Ta có:

    P\left( A_{1} \right) = 0,35, P\left( A_{2} \right) = 0,65, P\left( B|A_{1} \right) = 0,003, P\left( B|A_{2} \right) = 0,007

    P(B) = P\left( B|A_{1} \right).P\left( A_{1} \right) + P\left( B|A_{2} \right).P\left( A_{2} \right) = 0,0056

  • Câu 18: Thông hiểu
    Chọn đáp án chính xác

    Lớp 10A có 35 học sinh, mỗi học sinh đều giỏi ít nhất một trong hai môn Toán hoặc Văn. Biết rằng có 23 học sinh giỏi môn Toán và 20 học sinh giỏi môn Văn. Chọn ngẫu nhiên một học sinh của lớp 10A. Tính xác suất để học sinh được chọn "không giỏi môn Văn biết rằng học sinh đó giỏi môn Toán". (Làm tròn đến hàng phần trăm).

    Hướng dẫn:

    Trong số 23 học sinh giỏi Toán, có đúng 8 học sinh giỏi cả Toán và Văn nên số học sinh không giỏi Văn mà giỏi Toán là 23 - 8 = 15.

    Xác suất để học sinh được chọn "không giỏi môn Văn biết rằng học sinh đó giỏi môn Toán" là P = \frac{15}{23} \approx 0,65

  • Câu 19: Thông hiểu
    Tính xác suất của biến cố A

    Cho 2 biến cố A và B biết P\left( A|B \right) = 0, 08; P\left( \overline{A}|\overline{B} \right) = 0,63; P(B) = 0, 03. Khi đó xác suất xảy ra biến cố A là bao nhiêu?

    Hướng dẫn:

    Ta có: P(B) = 0,03 \Rightarrow P\left( \overline{B} \right) = 1 - 0,03 = 0,97.

    P\left( \overline{A}|\overline{B} \right) = 0,63 \Rightarrow P\left( A|\overline{B} \right) = 1 - 0,63 = 0,37.

    Theo công thức xác suất toàn phần:

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

    \Leftrightarrow P(A) = 0,03.0,08 + 0,97.0,37 = 0,3613.

  • Câu 20: Thông hiểu
    Tính xác suất người được chọn là đàn ông

    Được biết có 5\% đàn ông bị mù màu và 0,25\% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chon một người bị mù màu. Xác suất để người đó là đàn ông là bao nhiêu?

    Hướng dẫn:

    Gọi A là biến cố người được chọn là đàn ông, B là biến cố người được chọn mù màu.

    Theo đề bài ra ta có P\left( \left. \ B \right|A \right) = 0,05;P\left( \left. \ B \right|\overline{A} \right) = 0,0025.

    Vì số đàn ông bằng số phụ nữ nên ta có P(A) = P\left( \overline{A} \right) = 0,5.

    Áp dụng công thức Bayes ta có xác suất để chọn được một người đàn ông mù màu là:

    P\left( \left. \ A \right|B \right) =\frac{P(A).P\left( \left. \ B \right|A \right)}{P(A).P\left( \left. \ B \right|A \right) + P\left( \overline{A} \right).P\left( \left. \ B\right|\overline{A} \right)}

    = \frac{0,5.0,05}{0,5.0,05 + 0,5.0,0025} = \frac{20}{21}.

  • Câu 21: Thông hiểu
    Tính P(B)

    Cho hai biến cố A,\ B thỏa mãn P(A) = 0,4;\ P\left( A|B \right) = 0,5;\ P\left( \left. \ A \right|\overline{B} \right) = 0,1. Khi đó, P(B) bằng:

    Hướng dẫn:

    Đặt P(B) =x, suy ra P\left( \overline{B} \right) = 1 - x.

    Theo công thức xác suất toàn phần, ta có:

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

    \Leftrightarrow 0,4 = 0,5x + 0,1(1 - x)

    \Leftrightarrow 0,3 = 0,4x

    \Leftrightarrow x = 0,75

    Vậy P(B) = 0,75.

  • Câu 22: Thông hiểu
    Tính xác suất của biến cố

    Trong lễ khai giảng năm học mới, bạn An tham gia trò chơi gồm hai vòng. Xác suất thắng ở vòng chơi đầu tiên là 0,7. Nếu An thắng ở vòng thứ nhất thì xác suất thắng ở vòng hai là 0,8. Ngược lại, nếu An thua ở vòng thứ nhất thì xác suất thắng ở vòng hai là 0,4. Xác xuất để An thắng ở vòng chơi thứ hai là

    Hướng dẫn:

    Gọi biến cố A: “Bạn An thắng ở vòng thứ nhất”

    Biến cố B: “Bạn An thắng ở vòng thứ hai”

    Ta có sơ đồ hình cây biểu thị tình huống trên như sau:

    P(B) = P(A)P\left( B|A \right) + P\left(\overline{A} \right)P\left( B|\overline{A} \right)= 0,7.0,8 + 0,3.0,4 =0,68.

  • Câu 23: Thông hiểu
    Tính xác suất chọn được áo chất lượng cao

    Một công ty may có hai chi nhánh cùng sản xuất một loại áo, trong đó có 56\% áo ở chi nhánh I và 44\% áo ở chi nhánh II. Tại chi nhánh I có 75\% áo chất lượng cao và tại chi nhánh II có 68\% áo chất lượng cao (kích thước và hình dáng bề ngoài của các áo là như nhau). Chọn ngẫu nhiên 1 áo. Xác suất chọn được áo chất lượng cao là (làm tròn đến chữ số thập phân thứ hai)

    Hướng dẫn:

    Gọi A là biến cố áo được chọn là áo chất lượng cao. B là biến cố áo được chọn ở chi nhánh I và \overline{B} là biến cố áo được chọn ở chi nhánh II.

    Từ giải thiết ta có P(B) = 0,56, P\left( \left. \ A \right|B \right) = 0,75, P\left( \overline{B} \right) = 0,44, P\left( \left. \ A \right|\overline{B} \right) = 0,68.

    Theo công thức xác suất toàn phần ta có:

    P(A) = P(B).P\left( A\left| B\right.\ \right) + P\left( \overline{B} \right).P\left( \left. \ A\right|\overline{B} \right)

    = 0,56.0,75 + 0,44.0,68 = 0,7192 \approx0,72.

    Vậy xác suất chọn được áo chất lượng cao là 0,72.

  • Câu 24: Thông hiểu
    Chọn đáp án đúng

    Có hai chiếc hộp đựng 30 chiếc bút chì có hình dáng, kích thước giống nhau. Sau khi thống kê nhận được bảng số liệu sau:

    Lấy ngẫu nhiên một chiếc bút từ hộp I bỏ sang hộp II. Sau đó, lấy ngẫu nhiên một chiếc bút từ hộp II. Xác suất để chiếc bút lấy ra từ hộp II có màu xanh là

    Hướng dẫn:

    Gọi hai biến cố:

    A: “Lấy được bút xanh từ hộp I”;

    B: “Lấy được bút xanh từ hộp II”.

    Theo bài ra, ta có

    P(A) = \frac{15}{20} = \frac{3}{4} ; P\left( \overline{A} \right) = 1 - \frac{3}{4} = \frac{1}{4} ; P\left( B|A \right) = \frac{6}{11} ; P\left( B|\overline{A} \right) = \frac{5}{11}.

    Áp dụng công thức xác suất toàn phần, ta có

    P(B) = P(A)P\left( B|A \right) + P\left(\overline{A} \right)P\left( B|\overline{A} \right)=\frac{3}{4}.\frac{6}{11} + \frac{1}{4}.\frac{5}{11} =\frac{23}{44}.

  • Câu 25: Thông hiểu
    Chọn đáp án đúng

    Người ta điều tra thấy ở một địa phương nọ có 3\% tài xế sử dụng điện thoại di động khi lái xe. Người ta nhận thấy khi tài xế lái xe gây ra tai nạn thì có 21\% là do tài xế sử dụng điện thoại. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?

    Hướng dẫn:

    Ta gọi A là biến cố “Tài xế sử dụng điện thoại di động khi lái xe”, B là biến cố “Tài xế lái xe gây tai nạn”.

    Khi đó P\left( A \right) = 3\% = 0,03,P\left( {A|B} \right) = 21\% = 0,21.

    Theo công thức Bayes:

    P\left( B|A \right) = \frac{P( B)P\left(A|B \right)}{P(A)}

    \Rightarrow \frac{P\left( B|A \right)}{P(B)} = \frac{P\left( A|B \right)}{P(A)} = \frac{0,21}{0,03} = 7

    Vậy việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên 7 lần.

  • Câu 26: Thông hiểu
    Xác định P(B)

    Cho P(A) = 0,4; P\left( B|A \right) = 0,2 và P\left( B|\overline{A} \right) = 0,3. Giá trị của P(B) là

    Hướng dẫn:

    Vì P(A) = 0,4 nên P\left( \overline{A} \right) = 1 - 0,4 = 0,6.

    Theo công thức xác suất toàn phần ta có:

    P(B) = P(A).P\left( B|A \right) + P\left(\overline{A} \right).P\left( B|\overline{A} \right)= 0,4.0,2 + 0,6.0,3= 0,26.

  • Câu 27: Thông hiểu
    Tính xác suất để chọn thư rác

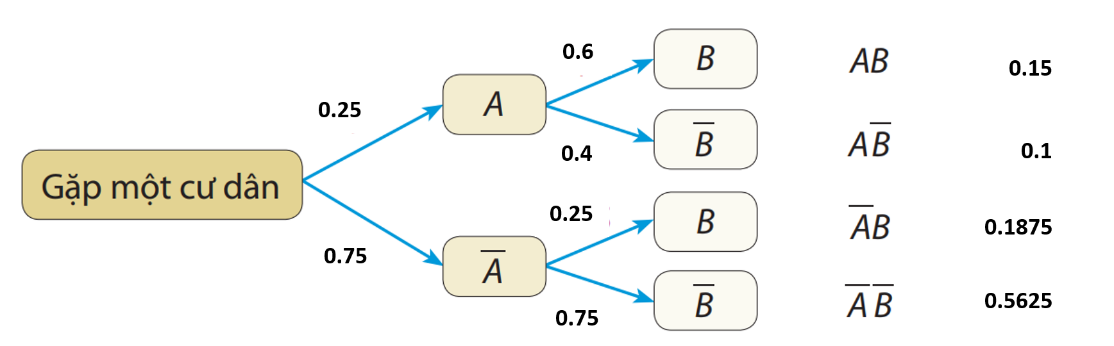
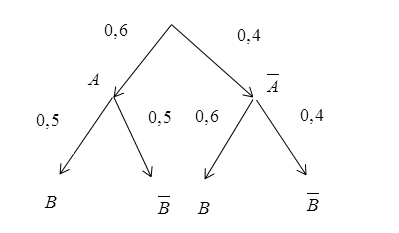
    Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3\%. Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác (kết quả làm tròn đến hàng phần nghìn).

    Hướng dẫn:

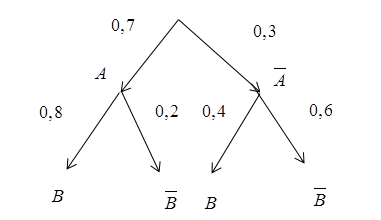
    Gọi A là biến cố: “Thư được chọn là thư rác”; B là biến cố: “Thư được chọn là bị chặn”.

    Ta có P(A) = 3\% = 0,03;

    P\left( \overline{A} \right) = 1 - P(A) = 1 - 0,03 = 0,97;

    P\left( B|A \right) = 0,95;\ \ \ P\left( B|\overline{A} \right) = 0,01.

    Công thức Bayes, ta có:

    P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(A).P\left( B|A \right) + P\left( \overline{A} \right).P\left( B|\overline{A} \right)}

    = \frac{0,03.0,95}{0,03.0,95 + 0,97.0,01}\approx 0,746.

0/27
27 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (100%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
Tải file làm trên giấy
1
76 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này