Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Ôn thi Đại học môn Toán - Chuyên đề: Tổ hợp và xác suất

Tài liệu ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại File: PDF

Phân loại: Tài liệu Tính phí

Ôn thi Đại học, THPT Quốc gia môn Toán - Chuyên đề: Tổ hợp và xác suất

Trong chương trình Toán THPT, chuyên đề tổ hợp và xác suất là một trong những nội dung quan trọng thuộc phần đại số và xác suất thống kê. Các bài toán liên quan đến quy tắc đếm, hoán vị, chỉnh hợp, tổ hợp và xác suất thường xuất hiện trong đề thi tốt nghiệp THPT với nhiều mức độ từ cơ bản đến vận dụng. Để giải quyết hiệu quả các dạng toán này, học sinh cần nắm vững công thức, hiểu rõ bản chất của từng phương pháp đếm và biết cách vận dụng linh hoạt trong từng tình huống cụ thể.

Bài viết “Ôn thi Đại học môn Toán – Chuyên đề: Tổ hợp và xác suất” được biên soạn nhằm hệ thống hóa toàn bộ các kiến thức trọng tâm cùng những dạng bài thường gặp trong chương trình Toán 12. Nội dung không chỉ giúp học sinh ôn tập lại các công thức quan trọng mà còn cung cấp nhiều bài tập tiêu biểu để rèn luyện tư duy logic và kỹ năng phân tích bài toán xác suất.

Tài liệu được xây dựng bám sát định hướng ra đề của Bộ Giáo dục và Đào tạo Việt Nam , giúp học sinh làm quen với cấu trúc câu hỏi trắc nghiệm và nâng cao khả năng xử lý bài toán nhanh chóng. Đây là nguồn tài liệu hữu ích hỗ trợ quá trình luyện đề, củng cố kiến thức và chuẩn bị cho kỳ thi THPT Quốc gia môn Toán.

VẤN ĐỀ 1: SỬ DỤNG CÔNG THỨC P_n, A^k_n, C^k_n

A. PHƯƠNG PHÁP GIẢI

1. Hoán vị

Số hoán vị của n phần tử: P_n = n!

2. Chỉnh hợp

Số chỉnh hợp: A^m_n = n(n - 1)(n - 2)...(n - m + 1)

Điều kiện: n ≥ m và n, m nguyên dương

3. Tổ hợp

B. ĐỀ THI

Bài 1: Đại học khối B năm 2008

Chứng minh rằng: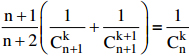

(n, k là các số nguyên dương, k ≤ n, C^k_n là số tổ hợp chập k của n phần tử

Giải:

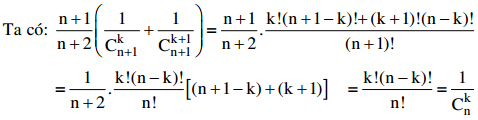
Bài 2: Đại học khối B năm 2006

Cho tập hợp A gồm n phần tử (n ≥ 4). Biết rằng số tập con gồm 4 phần tử của A bằng 20 lần số tập con gồm 2 phần tử của A. Tìm k thuộc {1, 2, ..., n} sao cho số tập con gồm k phần tử của A là lớn nhất.

Giải:

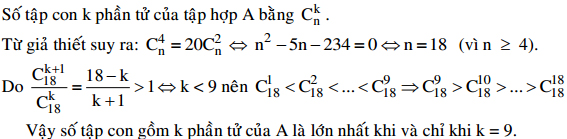
VẤN ĐỀ 2: PHÉP ĐẾM VÀ XÁC SUẤT

A. PHƯƠNG PHÁP GIẢI

I. Phép đếm

1. Nguyên tắc đếm

Có 2 biến cố A và B:

A có m cách xảy ra
B có n cách xảy ra
2 biến cố A và B cùng xảy ra có m × n cách
Biến cố A hoặc B xảy ra có m + n cách
Chú ý: Nguyên tắc trên có thể áp dụng cho nhiều biến cố

2. Chú ý:

Nếu thay đổi vị trí mà biến cố thay đổi ta có một hoán vị hoặc một chỉnh hợp
Nếu thay đổi vị trí mà biến cố không đổi ta có một tổ hợp

II. Xác suất

1. Không gian mẫu

Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra
Biến cố A là một tập con của không gian mẫu

2. Xác suất

Nếu các phần tử của không gian mẫu có cùng khả năng xảy ra, h là số phần tử của biến cố A, n là số phân tử của không gian mẫu. Xác suất để biến cố A xảy ra:

3. Các công thức

- Không gian mẫu E là biến cố chắc chắn xảy ra: p(E) = 1

- Biến cố Ø là biến cố không thể xảy ra: p(Ø) = 0

- Biến cố kéo theo A → B là biến cố A xảy ra thì biến cố B xảy ra: . P(A) ≤ P(B)

- A υ B là biến cố (A xảy ra hay B xảy ra). p(A υ B) = p(A) + p(B) - p(A ∩ B)

- A ∩ B là biến cố A và B cùng xảy ra

- Biến cố A và B đối lập nếu không cùng xảy ra. Khi đó, ta có: A ∩ B = Ø; p(A ∩ B) = 0; p(A υ B) = p(A) + p(B)

- Xác suất có điều kiện: Biến cố A xảy ra với điều kiện biến cố B đã xảy ra: hay p(A ∩ B) = p(B).p(A|B)

- Biến cố A và B độc lập nếu biến cố B có xảy ra hay không thì xác suất của A vẫn không đổi: p(A|B) = p(A), p(A ∩ B) = p(A)p(B)

B. ĐỀ THI

Bài 1: Đội thanh niên xung kích của một trường phổ thông có 12 học sinh, gồm 5 học sinh lơ̂p học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ, sao cho 4 học sinh này thuộc không quá 2 trong 3 lớp trên. Hỏi có bao nhiêu cách chọn như vậy?

Hướng dẫn giải

Số cách chọn 4 học sinh từ 12 học sinh đã cho là $C_{12}^{4} = 495$ .

Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau:

Lớp A có 2 học sinh, các lơ̂p B, C mỗi lớp có 1 học sinh. Số cách chọn là:

$C_{5}^{2} \cdot C_{4}^{1} \cdot C_{3}^{1} = 120$

Lớp B có 2 học sinh, các lớp mỗi lơ̂p có 1 học sinh. Số cách chọn là:

$C_{5}^{1} \cdot C_{4}^{2} \cdot C_{3}^{1} = 90$

Lớp C có 2 học sinh, các lơ̂p mỗi lơ̂p có 1 học sinh. Số cách chọn là:

$C_{5}^{1} \cdot C_{4}^{1} \cdot C_{3}^{2} = 60$

Số cách chọn 4 học sinh mà mỗi lơ̂p có ít nhất một học sinh là:

Vậy số cách chọn phải tìm là .

Bài 2: Một đội thanh niên tình nguyện có 15 người, gồm 12 nam và 3 nữ. Hỏi có bao nhiêu cách phân công đội thanh niên tình nguyện đó về giúp đđ 3 tỉnh miền núi, sao cho mỗi tỉnh có 4 nam và 1 nữ

Hướng dẫn giải

Có $C_{3}^{1}C_{12}^{4}$ cách phân công các thanh niên tình nguyện về tỉnh thứ nhất.

Với mỗi cách phân công các thanh niên tình nguyện về tỉnh thứ nhất thì có $C_{2}^{1}C_{8}^{4}$ cách phân công thanh niên tình nguyện về tỉnh thứ hai.

Với mỗi cách phân công các thanh niên tình nguyện về tỉnh thứ nhất và tỉnh thứ hai thì có $C_{1}^{1}C_{4}^{4}$ cách phân công thanh niên tình nguyện về tỉnh thứ ba.

Số cách phân công thanh niên tình nguyện về 3 tỉnh thỏa mãn yêu cầu bài toán là: $C_{3}^{1} \cdot C_{12}^{4} \cdot C_{2}^{1} \cdot C_{8}^{4} \cdot C_{1}^{1} \cdot C_{4}^{4} = 207900$ cách

(Còn tiếp)

-----------------------------------------------------------------------------

Chuyên đề tổ hợp và xác suất không chỉ giúp học sinh rèn luyện khả năng tư duy logic mà còn đóng vai trò quan trọng trong nhiều dạng bài trắc nghiệm của đề thi tốt nghiệp THPT môn Toán. Khi nắm vững các công thức và phương pháp đếm, học sinh có thể giải quyết các bài toán xác suất một cách nhanh chóng và chính xác.

Tài liệu “Ôn thi Đại học môn Toán – Chuyên đề: Tổ hợp và xác suất” giúp hệ thống lại những kiến thức trọng tâm cùng các dạng bài tiêu biểu thường gặp trong đề thi. Nội dung được xây dựng dựa trên định hướng ra đề của Bộ Giáo dục và Đào tạo Việt Nam , giúp học sinh làm quen với cấu trúc đề thi và cải thiện kỹ năng giải toán trắc nghiệm.

Việc kết hợp học lý thuyết với luyện tập thường xuyên sẽ giúp học sinh hiểu rõ bản chất của các bài toán tổ hợp và xác suất, đồng thời nâng cao khả năng vận dụng trong nhiều dạng bài khác nhau. Đây là nguồn tài liệu hữu ích hỗ trợ quá trình luyện đề, tổng ôn và chinh phục điểm cao trong kỳ thi THPT Quốc gia môn Toán.

Tải về

Chọn file muốn tải về: