Ôn thi Đại học môn Toán - Chuyên đề: Lượng giác
Ôn thi Đại học môn Toán - Chuyên đề: Lượng giác
Ôn thi Đại học môn Toán - Chuyên đề: Lượng giác tổng hợp các phương pháp giải bài tập lượng giác và các câu hỏi lượng giác trong đề thi đại học trong những năm trước. Bài tập có đáp án đi kèm, thuận tiện cho các bạn luyện tập và kiểm tra lại kiến thức. Hi vọng đây sẽ là tài liệu ôn thi THPT Quốc gia môn Toán hữu ích dành cho thầy cô và các bạn tham khảo.
Đề thi thử THPT Quốc gia năm 2017 môn Toán trắc nghiệm - Đề số 3
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc
VẤN ĐỀ 1: PHƯƠNG TRÌNH LƯỢNG GIÁC
A. PHƯƠNG PHÁP GIẢI
I. Phương trình lượng giác cơ bản
* cosx = cosα ↔ x = ± α + k2π
* 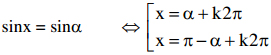
* tanx = tanα ↔ x = α + kπ
* cotx = cotα ↔ x = α + kπ
Với k thuộc Z
II. Phương trình bậc hai đối với một hàm số lượng giác
* asin2x + bsinx + c = 0. Đặt t = sinx, |t| ≤ 1
* acos2x + bcosx + c = 0. Đặt t = cosx, |t| ≤ 1
* atan2x + btanx + c = 0. Đặt t = tanx
* acot2x + bcotx + c = 0. Đặt t = cotx
III. Phương trình bậc nhất đối với sinx, cosx
asinx + bcosx = c (*)
Điều kiện có nghiệm: a2 + b2 ≥ c2
Cách 1:
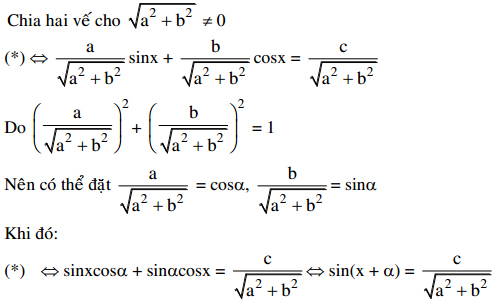
Cách 2:
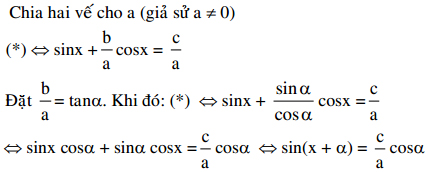
Cách 3:
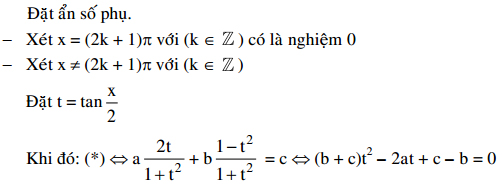
IV. Phương trình đối xứng: a(sinx + cosx) + bsinxcosx + c = 0
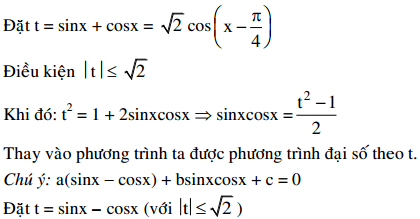
V. Phương trình đẳng cấp bậc 2 đối với sinx, cosx
asin2x + bsinxcosx + ccos2x = 0
- Xét cosx = 0 ↔ x = π/2 + kπ (k thuộc Z) có là nghiệm không?
- Xét cosx ≠ 0. Chia 2 vế cho cos2x ta thu được phương trình bậc 2 theo tanx.
Chú ý: Nếu là phương trình đẳng cấp bậc k đối với sinx, cosx thì ta xét cosx = 0 và xét cosx ≠ 0 chia 2 vế của phương trình cho coskx và ta thu được một phương trình bậc k theo tanx
Ôn thi Đại học môn Toán - Chuyên đề: Phương trình, Bất phương trình Đại số
Ôn thi Đại học môn Toán - Chuyên đề: Hình học giải tích trong mặt phẳng
B. ĐỀ THI
Bài 1: Đại học khối A năm 2011
Giải phương trình:c![]()
Giải:
Điều kiện: sinx # 0. Khi đó:
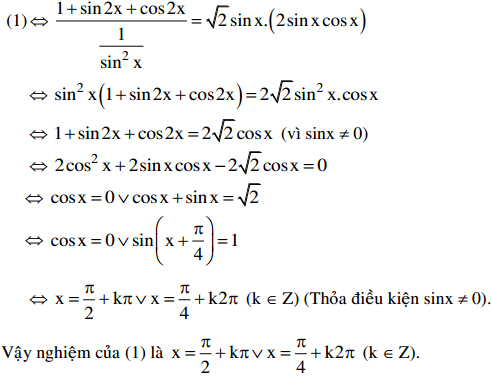
Bài 2: Đại học khối B năm 2011
Giải phương trình: sin2x.cosx + sinx.cosx = cos2x + sinx + cosx
Giải:
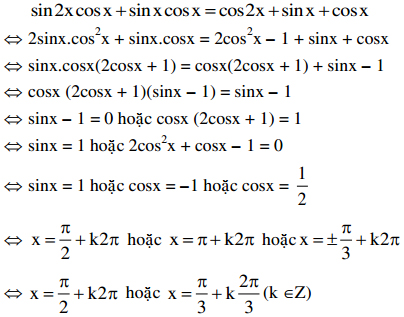
Bài 3: Đại học khối D năm 2011
Giải phương trình: 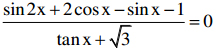

(Còn tiếp)


