Bài tập trắc nghiệm khảo sát hàm số (Có đáp án)
Bài tập trắc nghiệm khảo sát hàm số
Theo thông tin mới nhất, trong kỳ thi THPT Quốc gia và trong kỳ tuyển sinh 2021 sắp tới, môn Toán sẽ được thi theo hình thức trắc nghiệm với 50 câu hỏi. Thí sinh ngay từ bây giờ hãy luyện rèn cho mình thói quen giải nhanh các bài tập theo hình thức trắc nghiệm. Bài tập trắc nghiệm khảo sát hàm số có đáp án được VnDoc.com giới thiệu, sẽ là tài liệu ôn thi THPT Quốc gia môn Toán hữu ích dành cho các bạn tham khảo.
- Bài tập trắc nghiệm tính đơn điệu của hàm số
- Bài tập trắc nghiệm phương trình lượng giác
- Bài tập trắc nghiệm cực trị của hàm số và điểm uốn (Có đáp án)
- Ôn thi Đại học môn Toán - Chuyên đề: Khảo sát hàm số
VnDoc.com xin gửi tới bạn đọc bài viết Bài tập trắc nghiệm khảo sát hàm số (Có đáp án) để bạn đọc cùng tham khảo. Bài viết được VnDoc.com tổng hợp 15 câu hỏi trắc nghiệm về khảo sát đồ thị hàm số. Bộ câu hỏi có đáp án và lời giải kèm theo. Mời các bạn cùng tham khảo chi tiết và tải về tại đây.
Đề bài trắc nghiệm khảo sát hàm số
Câu 1: Đồ thị hàm số 
có tâm đối xứng là:
A. (3; 1) B. (1; 3) C. (1; 0) D. (0; 1)
Câu 2: Cho hàm số y = x3 - 3x2 + 3 xác định trên [1; 3]. Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì M + m bằng:
A. 2 B. 4 C. 8 D. 6
Câu 3: Cho hàm số 
có đồ thị (H). Tiếp tuyến của (H) tại giao điểm của (H) với trục Ox có phương trình là:
Câu 4: Cho hàm số 
có đồ thị (C) và đường thẳng d: y = x + m.
Với giá trị nào của m thì d cắt (C) tại 2 điểm phân biệt?
A. m < 2 B. m > 6 C. 2 D. m < 2 m > 6
Câu 5: Giá trị cực đại của hàm số y = x3 - 3x2 - 3x + 2 là:
A. -3 + 4√2 B. 3 - 4√2 C. 3 + 4√2 D. -3 - 4√2
Câu 6: Cho hàm số y = x3 - 3x2 + 2x - 1. Xét các mệnh đề:
I. Đồ thị có một điểm uốn.
II. Hàm số không có cực đại và cực tiểu.
III. Điểm uốn là tâm đối xứng của đồ thị
Mệnh đề nào đúng:
A. Chỉ I và II B. Chỉ II và III. C. Chỉ I và III. D. Cả I, II, III.
Câu 7: Cho hàm số y = 3x - 4x3 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm uốn của (C) có phương trình là:
A. y = -12x B. y = 3x C. y = 3x - 2 D. y = 0
Câu 8: Hàm số nào sau đây không có cực trị?
Câu 9: Điểm nào sau đây là điểm uốn của đồ thị hàm số y = x3 - 3x + 5
A. (0;5) B. (1;3) C. (-1;1) D. (0;0)
Câu 10: Hàm số y = x3 - 3x đạt giá trị nhỏ nhất trên [-2;2] khi x bằng:
A. -2 B. 1 C. -1 hay -2 D. 1 hay -2
Câu 11: Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
Câu 12: Cho hàm số y = x3 + 6x2 + 3(m + 2)x - m - 6 có cực đại, cực tiểu tại x1, x2 sao cho x1 < -1 < x2 thì giá trị của m là:
A. m > 1. B. m < 1. C. m > -1. D. m < -1.
Câu 13: Cho hàm số 
có đồ thị (C). Những điểm trên (C), tại đó tiếp tuyến có hệ số góc bằng 4 có tọa độ là:
A. (-1;-1) và (-3;7) B. (1;-1) và (3;-7)
C. (1;1) và (3;7) D. (-1;1) và (-3;-7)
Câu 14: Đặc điểm của đồ thị hàm số bậc ba là:
A. Luôn có trục đối xứng
B. Nhận đường thẳng nối hai cực trị làm trục đối xứng.
C. Luôn có tâm đối xứng.
D. Luôn nhận điểm cực trị làm tâm đối xứng.
Câu 15: Trong các hàm số sau đây, hàm số nào có giá trị nhỏ nhất trên tập xác định?
A. y = x3 - 3x2 - 6 B. y = x4 - 3x2 - 1
C. 
D. 
Đáp án bài tập trắc nghiệm khảo sát hàm số:
Câu 1: Đồ thị hàm số có tâm đối xứng là:
Đáp án: C. (1;0)
(C) có tiệm cận đứng là x = 1 và tiệm cận ngang y = 0.
Suy ra: Tâm đối xứng là: I(1;0).
Câu 2: Cho hàm số y = x3 - 3x2 + 3 xác định trên [1; 3]. Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì M + m bằng:
Đáp án: A. 2
y = x3 - 3x2 + 3 xác định trên [1;3]
y' = 3x2 - 6x = 3x(x - 2)
y' = 0 ↔ x = 0 hoặc x = 2
=> f(0) = 3; f(2) = -1; f(1) = 1; f(3) = 3
Suy ra:
GTLN: M = 3
GTNN: m = -1
Vậy: M + m = 2
Câu 3: Cho hàm số có đồ thị (H). Tiếp tuyến của (H) tại giao điểm của (H) với trục Ox có phương trình là:
Đáp án: D. y = 1/3 x - 1/3
(H) cắt Ox tại A(1;0)
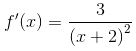
Suy ra: Hệ số góc tiếp tuyến tại A là: f'(1) = 1/3
Phương trình tiếp tuyến tại A là: y - 0 = 1/3(x - 1) => y = 1/3 x - 1/3
Câu 4: Cho hàm số có đồ thị (C) và đường thẳng d: y = x + m.
Với giá trị nào của m thì d cắt (C) tại 2 điểm phân biệt?
Đáp án: D. m < 2 m > 6
Phương trình hoành độ giao điểm:
\(\frac{2x + 3}{x + 2} = x + m
\Leftrightarrow x^{2} + mx + 2m - 3 = 0(*)(x \neq 2)\)
Để d cắt \((C)\) tại 2 điểm phân biệt \(\Leftrightarrow \left( \ ^{*}
\right)\) có 2 nghiệm \(\neq
2\)
\(\Leftrightarrow \left\{ \begin{matrix}
\Delta > 0 \\
f( - 2) \neq 0 \\
\end{matrix} \Leftrightarrow \left\{ \begin{matrix}
m^{2} - 8m + 12 > 0 \\
1 \neq 0 \\
\end{matrix} \Leftrightarrow m < 2 \vee m > 6
\right.\ \right.\)
Câu 5: Giá trị cực đại của hàm số y = x3 - 3x2 - 3x + 2 là:
Đáp án: A. -3 + 4√2
Câu 6: Cho hàm số y = x3 - 3x2 + 2x - 1. Xét các mệnh đề:
I. Đồ thị có một điểm uốn.
II. Hàm số không có cực đại và cực tiểu.
III. Điểm uốn là tâm đối xứng của đồ thị
Mệnh đề nào đúng?
Đáp án: C. Chỉ I và III.
\(\begin{matrix}
& \
& y = x^{3} - 3x^{2} - 3x + 2,D = R \\
& \ \Rightarrow y^{'} = 3x^{2} - 6x - 3 = 3\left( x^{2} - 2x -
1 \right) \\
& y^{'} = 0 \Leftrightarrow x^{2} - 2x - 1 = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 1 - \sqrt{2} \\
x = 1 + \sqrt{2} \\
\end{matrix} \right.\ \\
& y_{CD} = f(1 - \sqrt{2}) = - 3 + 4\sqrt{2} \\
& y = x^{3} - 3x^{2} + 2x - 1 \\
& y^{'} = 3x^{2} - 6x + 2 \\
& \Delta_{y^{'}}^{'} = 9 - 6 > 0 \\
\end{matrix}\)
Suy ra: Hàm số có cực đại và cực tiểu nên II sai.
I. III đúng (tính chất của hàm số bậc 3 )
Câu 7: Cho hàm số y = 3x - 4x3 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm uốn của (C) có phương trình là:
Đáp án: B. y = 3x
Câu 8: Hàm số nào sau đây không có cực trị?
Đáp án: D. Cả ba hàm số A, B, C
\(\begin{matrix}
& y = 3x - 4x^{3}(C) \\
& y^{'} = 3 - 12x^{2} \\
& y^{''} = - 24x \\
& y^{''} = 0 \Leftrightarrow x = 0 \Rightarrow y = 0 \\
\end{matrix}\)
Điểm uốn \(O(0;0) \Rightarrow f^{'}(0)
= 3\)
Phương trình tiếp tuyến tại điểm uốn là \(y
= 3x\)
\(y = - 2x^{3} + 1 \Rightarrow y^{'} =
- 6x^{2} \leq 0\text{~}\)
Suy ra hàm số nghịch biến
\(y = \frac{2x - 2}{x + 1} \Rightarrow
y^{'} = \frac{4}{(x + 1)^{2}} > 0\ \text{~}\)
Suy ra hàm số đồng biến
\(y = \frac{x^{2} + x - 3}{x + 2}
\Rightarrow y^{'} = \frac{x^{2} + 4x + 5}{(x + 2)^{2}} > 0\
\text{~}\)
Suy ra hàm số đồng biến
Cả ba hàm số không có cực trị.
Câu 9: Điểm nào sau đây là điểm uốn của đồ thị hàm số y = x3 - 3x + 5
Đáp án: A. (0; 5)
\(\begin{matrix}
& y = x^{3} - 3x + 5 \\
& \ \Rightarrow y^{'} = 3x^{2} - 3 \\
& y^{''} = 6x \\
& y^{''} = 0 \Leftrightarrow x = 0 \Rightarrow y = 5 \\
\end{matrix}\)
Vậy điểm uốn \((0;5)\)
Câu 10: Hàm số y = x3 - 3x đạt giá trị nhỏ nhất trên [-2;2] khi x bằng:
Đáp án: D. 1 hay -2
Câu 11:
Đáp án: B
Câu 12:
Đáp số: B. m<1.
\(\begin{matrix}
& y = x^{3} + 6x^{2} + 3(m + 2)x - m - 6 \\
& y^{'} = g(x) = 3x^{2} + 12x + 3(m + 2) \\
& y^{'} = 0\text{~} \\
\end{matrix}\)
Có hai nghiệm \(,x_{2} \Leftrightarrow
\Delta^{'} = 36 - 9(m + 2)\)
\(\Leftrightarrow 18 - 9m > 0
\Leftrightarrow m < 2(1)\)
Để hàm số đạt cực đại, cực tiểu tiểu tại \(x_{1},x_{2}\) sao cho: \(x_{1} < - 1 < x_{2}\)
\(\Leftrightarrow a.g( - 1) < 0
\Leftrightarrow 3(3m - 3) < 0 \Leftrightarrow m <
1(2)\)
Từ (1) và (2) suy ra: \(m <
1\) .
Câu 13:
Đáp số: A. (-1; -1) và (-3; 7)
Câu 14:
Đáp án: C. Luôn có tâm đối xứng.
Câu 15:
Đáp án: B.
-------------------------------------------------
Hy vọng rằng với bộ bài tập trắc nghiệm khảo sát hàm số có đáp án trên đây, bạn đã có thêm tư liệu ôn luyện hiệu quả cho các kỳ thi quan trọng. Đừng quên luyện tập thường xuyên để nắm vững kiến thức và nâng cao kỹ năng giải toán. Nếu bạn thấy tài liệu hữu ích, hãy chia sẻ với bạn bè và theo dõi website để cập nhật thêm nhiều đề trắc nghiệm Toán học hay khác!
