VnDoc.com

Ôn thi Đại học môn Toán - Chuyên đề: Hình học giải tích trong không gian Oxyz

Ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Ôn thi Đại học môn Toán: Hình học giải tích trong không gian Oxyz

Ôn thi Đại học môn Toán - Chuyên đề: Hình học giải tích trong không gian Oxyz tổng hợp các dạng bài tập toán hình học không gian và các bài tập về giải tích trong không gian Oxyz xuất hiện trong đề thi đại học các năm trước. Hi vọng tài liệu này sẽ giúp các bạn luyện thi THPT Quốc gia theo chuyên đề hiệu quả.

VẤN ĐỀ 1: MẶT PHẲNG VÀ ĐƯỜNG THẲNG

A. PHƯƠNG PHÁP GIẢI

I. Tọa độ

II. Mặt phẳng

- Vecto pháp tuyến của mặt phẳng là vecto khác vecto 0 và có giá vuông góc mặt phẳng.

- Phương trình tổng quát: (α): Ax + By + Cz + D = 0 (A² + B² + C²) # 0

- Ôn thi đại học môn Toán chuyên đề hình học giải tích trong không gian Oxyz

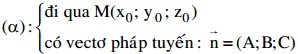
→ (α): A(x - x_o) + B(y - y_o) + C(z - z_o) = 0

- Mặt phẳng chắn: (α) cắt Ox, Oy, Oz lần lượt tại A $\left( \alpha \right):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ $(α) : \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ (a; 0; 0), B(0; b; 0), C(0; 0; c), (a, b, c # 0)

- Mặt phẳng đặc biệt: (Oxy): z = 0; (Oxz): y = 0, (Oyz): x = 0

III. Đường thẳng

Vector chỉ phương của đường thẳng là vecto khác 0 và có giá cùng phương với đường thẳng
Đường thẳng d đi qua điểm $M\left( {{x_0};{y_0};{z_0}} \right)$ $M (x_{0}; y_{0}; z_{0})$ và có vecto chỉ phương $\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right)$ $\vec{a} = (a_{1}; a_{2}; a_{3})$
Phương trình tham số: $\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}$ $\frac{x - x_{0}}{a_{1}} = \frac{y - y_{0}}{a_{2}} = \frac{z - z_{0}}{a_{3}}$ với ${{a_1};{a_2};{a_3} \ne 0}$ $a_{1}; a_{2}; a_{3} \neq 0$
Đường thẳng đặc biệt: $Ox:\left\{ \begin{gathered} y = 0 \hfill \\ z = 0 \hfill \\ \end{gathered} \right.;Oy:\left\{ \begin{gathered} x = 0 \hfill \\ z = 0 \hfill \\ \end{gathered} \right.;Oz:\left\{ \begin{gathered} x = 0 \hfill \\ y = 0 \hfill \\ \end{gathered} \right.$ $O x : {\begin{matrix} y = 0 \\ z = 0 \end{matrix}; O y : {\begin{matrix} x = 0 \\ z = 0 \end{matrix}; O z : {\begin{matrix} x = 0 \\ y = 0 \end{matrix}$

B. ĐỀ THI

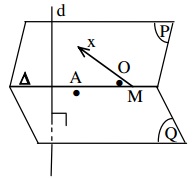
Bài 1: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và đường thẳng d: . Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với đường thẳng d và cắt trục Ox.

Giải:

Cách 1:

Gọi M là giao điểm của Δ với trục Ox => M(m; 0; 0) => $\overrightarrow {AM} = \left( {m - 1; - 2; - 3} \right)$ $\vec{A M} = (m - 1; - 2; - 3)$

Vecto chỉ phương của đường thẳng d là $\overrightarrow a = \left( {2;1; - 2} \right)$ $\vec{a} = (2; 1; - 2)$

$\Delta \bot d$ $Δ ⊥ d$ suy ra $aM \bot d$ $a M ⊥ d$

$\Leftrightarrow \overrightarrow {AM} .\overrightarrow a = 0 \Leftrightarrow 2\left( {m - 1} \right) + 1.\left( { - 2} \right) - 2.\left( { - 3} \right) = 0$ $\Leftrightarrow \vec{A M} . \vec{a} = 0 \Leftrightarrow 2 (m - 1) + 1. (- 2) - 2. (- 3) = 0$ $\Leftrightarrow m = 1$ $\Leftrightarrow m = 1$

Đường thẳng Δ đi qua M nhận $\overrightarrow {AM} = \left( { - 2; - 2; - 3} \right)$ $\vec{A M} = (- 2; - 2; - 3)$ làm vecto chỉ phương nên có phương trình là: $\frac{{x - 1}}{2} = \frac{{y - 2}}{2} = \frac{{z - 3}}{3}$ $\frac{x - 1}{2} = \frac{y - 2}{2} = \frac{z - 3}{3}$

Cách 2:

Δ đi qua A và cắt trục Ox nên Δ nằm trên mặt phẳng (P) đi qua A và chứa trục Ox.

Δ đi qua A và vuông góc với d nên Δ nằm trên mặt phẳng (Q) đi qua A.

Ta có:

Vecto pháp tuyến của (P) là $\overrightarrow {{n_{\left( P \right)}}} = \left[ {\overrightarrow {OA} ;\overrightarrow i } \right]$ $\vec{n_{(P)}} = [\vec{O A}; \vec{i}]$

Vecto pháp tuyến của (Q) là: $\overrightarrow {{n_{\left( Q \right)}}} = \overrightarrow {{a_d}}$ $\vec{n_{(Q)}} = \vec{a_{d}}$

Δ = (P) ∩ (Q) => vecto chỉ phương của Δ là: $\overrightarrow {{a_\Delta }} = \left[ {\overrightarrow {{n_{\left( P \right)}}} ;\overrightarrow {{n_{\left( Q \right)}}} } \right]$ $\vec{a_{Δ}} = [\vec{n_{(P)}}; \vec{n_{(Q)}}]$

Cách 3:

Mặt phẳng (Q) đi qua A và vuông góc với d → (Q): 2x + y – 2z + 2 = 0.
Gọi M là giao điểm của Ox và (Q) → M(–1; 0; 0).
Véctơ chỉ phương của Δ là:

Bài 2: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $\Delta :\frac{{x + 2}}{1} = \frac{{y - 1}}{3} = \frac{{z + 5}}{{ - 2}}$ $Δ : \frac{x + 2}{1} = \frac{y - 1}{3} = \frac{z + 5}{- 2}$ và hai điểm A(-2; 1; 1), B(-3; -1; 2). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho tam giác MAB có diện tích bằng 3√5.

Giải

Đường thẳng Δ đi qua E(-2; 1; -5) và có véctơ chỉ phương nên có phương trình tham số là: $\left\{ \begin{gathered} x = - 2 + t \hfill \\ y = 1 + 3t \hfill \\ z = - 5 - 2t \hfill \\ \end{gathered} \right.;\left( {t \in \mathbb{R}} \right)$ ${\begin{matrix} x = - 2 + t \\ y = 1 + 3 t \\ z = - 5 - 2 t \end{matrix}; (t \in R)$

M∈Δ => M(-2 + t; 1+3t; -5-2t)

$\left\{ \begin{gathered} \overrightarrow {AB} = \left( { - 1; - 2;1} \right) \hfill \\ \overrightarrow {AM} = \left( {t;3t; - 6 - 2t} \right) \hfill \\ \end{gathered} \right. \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AM} } \right] = \left( {t + 12; - t - 6; - t} \right)$ ${\begin{matrix} \vec{A B} = (- 1; - 2; 1) \\ \vec{A M} = (t; 3 t; - 6 - 2 t) \end{matrix} \Rightarrow [\vec{A B}; \vec{A M}] = (t + 12; - t - 6; - t)$

${S_{MAB}} = 3\sqrt 5 \Leftrightarrow \frac{1}{2}\left[ {\overrightarrow {AB} ;\overrightarrow {AM} } \right] = 3\sqrt 5$ $S_{M A B} = 3 \sqrt{5} \Leftrightarrow \frac{1}{2} [\vec{A B}; \vec{A M}] = 3 \sqrt{5}$

$\Leftrightarrow \sqrt {{{\left( {t + 12} \right)}^2} + {{\left( {t + 6} \right)}^2} + {t^2}} = 3\sqrt 5$ $\Leftrightarrow \sqrt{{(t + 12)}^{2} + {(t + 6)}^{2} + t^{2}} = 3 \sqrt{5}$

$\Leftrightarrow 3{t^2} + 36t = 0 \Leftrightarrow \left[ \begin{gathered} t = 0 \hfill \\ t = - 12 \hfill \\ \end{gathered} \right.$ $\Leftrightarrow 3 t^{2} + 36 t = 0 \Leftrightarrow [\begin{matrix} t = 0 \\ t = - 12 \end{matrix}$

Vậy M(-2; 1; -5) hoặc M(-14; -35; 19).

Bài 3: Trong không gian với hệ tọa độ Oxyz cho đường thẳng $\Delta :\frac{{x + 2}}{1} = \frac{{y - 2}}{1} = \frac{z}{{ - 1}}$ $Δ : \frac{x + 2}{1} = \frac{y - 2}{1} = \frac{z}{- 1}$ và mặt phẳng $\left( P \right):x + 2y - 3z + 4 = 0$ $(P) : x + 2 y - 3 z + 4 = 0$ . Viết phương trình đường thẳng d nằm trong (P) sao cho d cắt và vuông góc với đường thẳng Δ.

Hướng dẫn giải

Tọa độ điểm I của Δ và (P) thỏa mãn hệ phương trình:

$\left\{ \begin{gathered} \frac{{x + 2}}{1} = \frac{{y - 2}}{1} = \frac{z}{{ - 1}} \hfill \\ x + 2y - 3z + 4 = 0 \hfill \\ \end{gathered} \right. \Rightarrow I\left( { - 3;1;1} \right)$ ${\begin{matrix} \frac{x + 2}{1} = \frac{y - 2}{1} = \frac{z}{- 1} \\ x + 2 y - 3 z + 4 = 0 \end{matrix} \Rightarrow I (- 3; 1; 1)$

Vecto pháp tuyến của (P) $\overrightarrow n = \left( {1;2; - 3} \right)$ $\vec{n} = (1; 2; - 3)$ , vecto chỉ phương của Δ: $\overrightarrow u = \left( {1;1; - 1} \right)$ $\vec{u} = (1; 1; - 1)$

Đường thẳng d cần tìm qua I và có một vecto chỉ phương: $\left\{ \begin{gathered} \overrightarrow {{n_{\left( {{P_1}} \right)}}} = \left( {1;2;3} \right) \hfill \\ \overrightarrow {{n_{\left( {{P_2}} \right)}}} = \left( {3;2; - 1} \right) \hfill \\ \end{gathered} \right.$ ${\begin{matrix} \vec{n_{(P_{1})}} = (1; 2; 3) \\ \vec{n_{(P_{2})}} = (3; 2; - 1) \end{matrix}$

Phương trình d là: $\left\{ \begin{gathered} x = - 3 + t \hfill \\ y = 1 - 2t \hfill \\ z = 1 - t \hfill \\ \end{gathered} \right.;\left( {t \in \mathbb{R}} \right)$ ${\begin{matrix} x = - 3 + t \\ y = 1 - 2 t \\ z = 1 - t \end{matrix}; (t \in R)$ .

Bài 4. Trong không gian với hệ tọa độ Oxyz cho các mặt phẳng $\left( {{P_1}} \right):x + 2y + 3z + 4 = 0$ $(P_{1}) : x + 2 y + 3 z + 4 = 0$ và $\left( {{P_2}} \right):3x + 2y - z + 1 = 0$ $(P_{2}) : 3 x + 2 y - z + 1 = 0$ . Viết phương trình mặt phẳng (P) đi qua điểm A(1;1;1) vuông góc với mặt phẳng $\left( {{P_1}} \right)$ $(P_{1})$ và $\left( {{P_2}} \right)$ $(P_{2})$ .

Hướng dẫn giải

Vecto pháp tuyến của hai mặt phẳng $\left( {{P_1}} \right)$ $(P_{1})$ và $\left( {{P_2}} \right)$ $(P_{2})$ là: $\left\{ \begin{gathered} \overrightarrow {{n_{\left( {{P_1}} \right)}}} = \left( {1;2;3} \right) \hfill \\ \overrightarrow {{n_{\left( {{P_2}} \right)}}} = \left( {3;2; - 1} \right) \hfill \\ \end{gathered} \right.$ ${\begin{matrix} \vec{n_{(P_{1})}} = (1; 2; 3) \\ \vec{n_{(P_{2})}} = (3; 2; - 1) \end{matrix}$

Gọi (P) vuông góc với hai mặt phẳng $\left( {{P_1}} \right)$ $(P_{1})$ và $\left( {{P_2}} \right)$ $(P_{2})$

Suy ra (P) có một vecto pháp tuyến $\Rightarrow \overrightarrow {{n_{\left( P \right)}}} = \left[ {\overrightarrow {{n_{\left( {{P_1}} \right)}}} ;\overrightarrow {{n_{\left( {{P_2}} \right)}}} } \right] = - 2\left( {4; - 5;2} \right)$ $\Rightarrow \vec{n_{(P)}} = [\vec{n_{(P_{1})}}; \vec{n_{(P_{2})}}] = - 2 (4; - 5; 2)$

Mặt khác (P) đi qua A(1;1;1) nên phương trình mặt phẳng:

(P): 4(x-1) - 5(y - 1)+2(z-1) = 0

Hay (P): 4x - 5y + 2z - 1 = 0

Bài 5: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;1;1), B(0;2;1) và trọng tâm G(0;2;-1). Viết phương trình đường thẳng Δ đi qua điểm C và vuông góc với mặt phẳng (ABC).

Hướng dẫn giải

Ta có G là trọng tâm tam giác ABC khi đó tọa độ điểm C(-1;3;-4)

Lại có: $\left\{ \begin{gathered} \overrightarrow {AB} = \left( { - 1;1;1} \right) \hfill \\ \overrightarrow {AC} = \left( { - 2;2; - 4} \right) \hfill \\ \end{gathered} \right.$ ${\begin{matrix} \vec{A B} = (- 1; 1; 1) \\ \vec{A C} = (- 2; 2; - 4) \end{matrix}$

Đường thẳng Δ vuông góc với mặt phẳng (ABC) nên có một vecto chỉ phương $\overrightarrow a = \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = - 6\left( {1;1;0} \right)$ $\vec{a} = [\vec{A B}; \vec{A C}] = - 6 (1; 1; 0)$

Mặt khác đường thẳng Δ đi qua điểm C nên phương trình đường thẳng cần tìm là: $\Delta :\left\{ \begin{gathered} x = - 1 + t \hfill \\ y = 3 + t \hfill \\ z = - 4 \hfill \\ \end{gathered} \right.;\left( {t \in \mathbb{R}} \right)$ $Δ : {\begin{matrix} x = - 1 + t \\ y = 3 + t \\ z = - 4 \end{matrix}; (t \in R)$

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

------------------------------------------------------

Qua bài viết, bạn đã nắm được các kiến thức chuyên đề Hình học giải tích trong không gian Oxyz một cách dễ hiểu và chính xác. Đây là nền tảng quan trọng để viết phương trình đường thẳng, giải các bài toán hình học không gian nâng cao. Hãy luyện tập thường xuyên với các ví dụ và bài tập tương tự để thành thạo hơn. Đừng quên lưu lại bài viết để ôn tập khi cần nhé!

Chia sẻ, đánh giá bài viết

61

68.917

Bài trước

Bài sau

Chia sẻ bởi:
Đen2017

Tải về

Chọn file muốn tải về:

Ôn thi Đại học môn Toán - Chuyên đề: Hình học giải tích trong không gian Oxyz

1,1 MB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!