Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2 gồm nhiều đề thi thử THPT Quốc gia môn Toán năm 2016 có đáp án đi kèm. Đây là tài liệu ôn tập môn Toán hữu ích dành cho các bạn học sinh lớp 12, các bạn thí sinh tự do, giúp các bạn chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học 2016 hiệu quả. Mời các bạn tham khảo.

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 3

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

Bộ đề thi thử THPT Quốc gia năm 2016 môn Ngữ văn - Số 1

Các chuyên đề luyện thi THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Lam Kinh, Thanh Hóa (Lần 1)

Câu 1 (2 điểm). Cho hàm số

a. Khảo sát và vẽ đồ thị (C) của hàm số.

b. Tìm điểm M trên (C) để khoảng cách từ M đến tiệm cận đứng của đồ thị (C) bằng khoảng cách từ M đến trục Ox.

Câu 2 (1 điểm).

a. Giải phương trình: √3sin2x - cos2x = 4sinx - 1.

b. Giải bất phương trình: 2log₃(x - 1) + log_√3(2x - 1) ≤ 2.

Câu 3 (0.5 điểm). Tính nguyên hàm sau:

Câu 4 (1.5 điểm).

a. Tìm số hạng chứa x³ trong khai triển của .

b. Một ngân hàng đề thi gồm 20 câu hỏi. Mỗi đề thi gồm 4 câu được lấy ngẫu nhiên từ 20 câu hỏi trên. Thí sinh A đã học thuộc 10 câu trong ngân hàng đề thi. Tìm xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc.

Câu 5 (1 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi I là trung điểm AB, H là giao điểm của BD với IC. Các mặt phẳng (SBD) và (SIC) cùng vuông góc với đáy. Góc giữa (SAB) và (ABCD) bằng 60^o. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và IC.

Câu 6 (1 điểm). Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại B, BC = 2BA. Gọi E, F lần lượt là trung điểm của BC, AC. Trên tia đối của tia FE lấy điểm M sao cho FM = 3FE. Biết điểm M có tọa độ (5; -1), đường thẳng AC có phương trình 2x + y - 3 = 0, điểm A có hoành độ là số nguyên. Xác định tọa độ các đỉnh của tam giác ABC.

Câu 7 (1 điểm). Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cà các cạnh đều bằng a .Tính thể tích của hình lăng trụ và diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.

Câu 8 (1 điểm). Giải hệ phương trình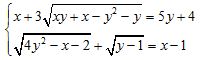

Câu 9 (1 điểm). Cho là độ dài ba cạnh của một tam giác thỏa mãn Tìm giá trị nhỏ nhất của biểu thức

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Lý Tự Trọng, Nam Định (Lần 1)

Câu 1 (2,0 điểm). Cho hàm số (1).

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
2. Tìm điểm M thuộc đồ thi (C) sao cho khoảng cách từ M đến đến trục Oy bằng 2 lần khoảng cách từ M đến đường tiệm cận ngang của đồ thị hàm số (1).

Câu 2 (1,0 điểm). Giải phương trình: 2cosx.cos2x = 2 - 2sin²x + cos3x.

Câu 3 (1,0 điểm). Tính nguyên hàm: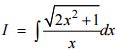

Câu 4 (1,0 điểm).

1. Giải phương trình: log_1/4(2x² - 3x + 1) + 1/2log₂(x - 1)² = 1/2.
2. Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = 8lnx - x² trên đoạn [1;e].

Câu 5 (1.0 điểm). Một hộp chứa 4 quả cầu màu đỏ, 5 quả cầu màu xanh và 7 quả cầu màu vàng. Lấy ngẫu nhiên cùng lúc ra 4 quả cầu từ hộp đó. Tính xác suất sao cho 4 quả cầu được lấy ra có đủ 3 màu, có đúng một quả cầu màu đỏ và có không quá hai quả cầu màu vàng.

Câu 6 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = a, AD = 2a, tam giác SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SD. Tính thể tích khối chóp S.ACD và khoảng cách giữa hai đường thẳng AI và SC.

Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD biết AB = 3/2AD. Gọi F là điểm thuộc đoạn thẳng BC sao cho BF = 3/4BC. Đường tròn (T) ngoại tiếp tam giác ABF có phương trình 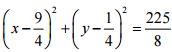. Đường thẳng d đi qua hai điểm A, C có phương trình 3x + 11y - 2 = 0. Tìm tọa độ đỉnh C biết điểm A có hoành độ âm.

Câu 8 (1.0 điểm). Giải hệ phương trình: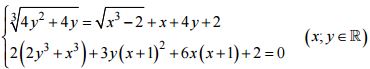

Câu 9 (1.0 điểm). Cho a, b, c là ba số thực dương thỏa mãn a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức:

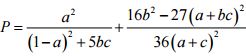
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành 1, Bắc Ninh (Lần 1)

Câu 1 (2,5 điểm).

1. Cho hàm số: (C)

a) Khảo sát sự biến thiên và vẽ đồ thị (C).

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có tung độ bằng 1.

2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x³ + 3x² - 9x + 1 trên đoạn [- 2; 2].

Câu 2 (0,5 điểm). Giải phương trình: 4sinx + cosx = 2 + sin2x

Câu 3 (1,5 điểm).

a) Giải phương trình: 5^2x - 24.5^x-1 - 1 = 0

b) Tìm hàm số f(x) biết và f(0) = 1.

Câu 4 (1,0 điểm). Trong không gian tọa độ Oxyz cho hình lập phương ABCD.A'B'C'D' có đỉnh A trùng với gốc toạ độ O, đỉnh B(1;1;0), D( 1;-1;0). Tìm tọa độ đỉnh A' biết A' có cao độ dương và viết phương trình mặt cầu ngoại tiếp hình lập phương ABCD.A'B'C'D'.

Câu 5 (0,5 điểm). Trường trung học phổ thông Thuận Thành số 1 có tổ Toán gồm 15 giáo viên trong đó có 8 giáo viên nam, 7 giáo viên nữ; Tổ Lý gồm 12 giáo viên trong đó có 5 giáo viên nam, 7 giáo viên nữ. Chọn ngẫu nhiên mỗi tổ 2 giáo viên đi dự tập huấn chuyên đề dạy học tích hợp. Tính xác suất sao cho trong các giáo viên được chọn có 2 nam và 2 nữ.

Câu 6 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA ⊥ (ABCD). Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ D đến mặt phẳng (SBM) với M là trung điểm của CD biết góc giữa SC và mặt phẳng chứa đáy là α với tanα = 1/√5.

Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có chân đường phân giác hạ từ đỉnh A là D(1;-1). Phương trình tiếp tuyến tại A của đường tròn ngoại tiếp tam giác ABC có phương trình x + 2y – 7 =0. Giả sử điểm M(13/5; -1/5) là trung điểm của BD. Tìm tọa độ các điểm A,C biết A có tung độ dương.

Câu 8 (1,0 điểm). Giải hệ phương trình sau

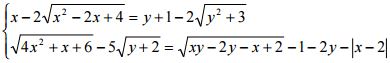
Câu 9 (1,0 điểm) Cho các số thực dương a, b, c thỏa mãn ab ≥ 1; c(a + b + c) ≥ 3. Tìm giá trị nhỏ nhất của biểu thức:

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Lý Thái Tổ, Bắc Ninh (Lần 2)

Câu 1 (2,0 điểm). Cho hàm số: (1) với m là tham số.

a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1.

b. Tìm tất cả các giá trị m để đường thẳng d: y = -2x + m cắt đồ thị của hàm số (1) tại hai điểm phân biệt có hoành độ x₁, x₂ sao cho |4(x₁ + x₂) - 6x₁x₂| = 21.

Câu 2 (1,0 điểm).

a. Giải phương trình: sin2x + 1 = cosx - cos2x.

b. Giải bất phương trình: log₂(x - 1) ≤ log_1/2 (x + 3) + 5.

Câu 3 (1,0 điểm). Tính nguyên hàm:

Câu 4 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A(3; 2) có tâm đường tròn ngoại tiếp là I(2; -1) và điểm B nằm trên đường thẳng d có phương trình: x - y - 7 = 0. Tìm tọa độ đỉnh B, C.

Câu 5 (1,0 điểm).

a. Cho tanα = -1/2 với -π/2 < α < 0. Tính giá trị của biểu thức: A = √5cosα - 5sin2α.

b. Cho X là tập hợp gồm 6 số tự nhiên lẻ và 4 số tự nhiên chẵn. Chọn ngẫu nhiên từ tập X ba số tự nhiên. Tính xác suất chọn được ba số tự nhiên có tích là một số chẵn.

Câu 6 (1,0 điểm). Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi cạnh a, góc BAD = 120⁰ và AC' = a√5. Tính thể tích khối lăng trụ ABCD.A'B'C'D' và khoảng cách giữa hai đường thẳng AB' và BD theo a.

Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có hình chiếu vuông góc của A lên đường thẳng BD là H(-6/5; 7/5), điểm M(-1; 0) là trung điểm cạnh BC và phương trình đường trung tuyến kẻ từ A của tam giác ADH có phương trình là 7x + y - 3 = 0. Tìm tọa độ các đỉnh của hình chữ nhật ABCD.

Câu 8 (1,0 điểm). Giải phương trình:

Câu 9 (1,0 điểm). Cho x, y, z là ba số dương thỏa mãn:

Tìm giá trị lớn nhất của biểu thức:

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Triệu Sơn 1, Thanh Hóa (Lần 1)

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x⁴ - 2x² + 1.

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [2;5].

Câu 3 (1,0 điểm).

a) Giải phương trình cos2x - 3sinx - 2 = 0.

b) Giải bất phương trình log₂(2x - 1) - log_1/2(x - 2) ≤ 1.

Câu 4 (1,0 điểm). Tìm số hạng chứa x³ trong khai triển nhị thức Niu - tơn của biểu thức (√x - 2/x)ⁿ, x < 0. Trong đó n là số tự nhiên thỏa mãn A²_n - 2C¹_n = 180.

Câu 5 (1,0 điểm). Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' có A(1; 1; 1), B(1; 2; 1), C(1; 1; 2) và A'(2; 2; 1). Tìm tọa độ các đỉnh B', C' và viết phương trình mặt cầu đi qua bốn điểm A, B, C, A'.

Câu 6 (1,0 điểm).

a) Cho cosα = 3/5. Tính giá trị của biểu thức P = cos²α/2 - cos2α.

b) Đội dự tuyển học sinh giỏi giải toán trên máy tính cầm tay môn toán của một trường phổ thông có 4 học sinh nam khối 12, 2 học sinh nữ khối 12 và 2 học sinh nam khối 11. Để thành lập đội tuyển dự thi học sinh giỏi giải toán trên máy tính cầm tay môn toán cấp tỉnh nhà trường cần chọn 5 em từ 8 em học sinh trên. Tính xác suất để trong 5 em được chọn có cả học sinh nam và học sinh nữ, có cả học sinh khối 11 và học sinh khối 12.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có SA vuông góc với mặt đáy (ABCD), đáy ABCD là hình chữ nhật có AD = 3a, AC = 5a, góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 45⁰. Tính theo a thể tích khối chóp S.ABCD và tính góc giữa đường thẳng SD và mặt phẳng (SBC).

Câu 8 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD vuông tại A, B và AD = 2BC. Gọi H là hình chiếu vuông góc của điểm A lên đường chéo BD và E là trung điểm của đoạn HD. Giả sử H(-1;3), phương trình đường thẳng AE: 4x + y + 3 = 0 và C(5/4; 4). Tìm tọa độ các đỉnh A, B và D của hình thang ABCD.

Câu 9 (1,0 điểm). Giải bất phương trìnhtrên tập hợp số thực.

Câu 10 (1,0 điểm). Cho a, b, c là các số thực không âm thỏa mãn a²b² + c²b² + 1 ≤ 3b. Tìm giá trị nhỏ nhất của biểu thức