Tính nhanh nguyên hàm - tích phân bằng máy tính Casio
Tính nhanh nguyên hàm - tích phân bằng máy tính Casio
Tính nhanh nguyên hàm - tích phân bằng máy tính Casio là tài liệu ôn thi THPT Quốc gia môn Toán hay dành cho quý thầy cô và các em tham khảo.
HƯỚNG DẪN SỬ DỤNG MÁY TÍNH CASIO
* Chỉnh máy:
- Sai số cực nhỏ 9 chữ số thập phân - Bấm: Shift – mod - 9
- Thông thường đơn vị rad - Bấm: Shift – mod - 4
Dạng 1: Tìm nguyên hàm F(x) của hàm số f(x):
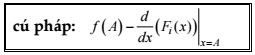
- Trong đó f(A): gá trị của f(x) tại x = A (A là hằng số bất kì thuộc tập xác định và A lấy giá trị bé 0,1; 0,2; ....;1; 1,1)
- Fi(x): các kết quả nguyên hàm.
Ví dụ:  \(\int_{}^{}\ \frac{5\left( x^{2}
+ x \right)}{\sqrt{2x + 1}}dx;x > - \frac{1}{2}\) bằng:
\(\int_{}^{}\ \frac{5\left( x^{2}
+ x \right)}{\sqrt{2x + 1}}dx;x > - \frac{1}{2}\) bằng:
A. ![]() \(\left( x^{2} + x + 1 \right)\sqrt{2x +
1} + C\) B.
\(\left( x^{2} + x + 1 \right)\sqrt{2x +
1} + C\) B. ![]() \(\left( x^{2} - x + 1 \right)\sqrt{2x +
1} + C\)
\(\left( x^{2} - x + 1 \right)\sqrt{2x +
1} + C\)
C. ![]() \(\left( x^{2} + x - 1 \right)\sqrt{2x +
1} + C\) D.
\(\left( x^{2} + x - 1 \right)\sqrt{2x +
1} + C\) D. ![]() \(\left( x^{2} - x - 1 \right)\sqrt{2x +
1} + C\)
\(\left( x^{2} - x - 1 \right)\sqrt{2x +
1} + C\)
Hướng dẫn giải
Bước 1: Nhập:  \(\frac{5\left( A^{2} + A
\right)}{\sqrt{2A + 1}} - \left. \ \frac{d}{dx}\left( x^{2} + x + 1
\right)\sqrt{2x + 1} \right|_{x = A}\) (RCL- A ; Shit
\(\frac{5\left( A^{2} + A
\right)}{\sqrt{2A + 1}} - \left. \ \frac{d}{dx}\left( x^{2} + x + 1
\right)\sqrt{2x + 1} \right|_{x = A}\) (RCL- A ; Shit ![]() \(\left. \
\int_{\square}^{\square}\mspace{2mu}\mspace{2mu}\square
\right)\)
\(\left. \
\int_{\square}^{\square}\mspace{2mu}\mspace{2mu}\square
\right)\)
Bước 2: Gán ![]() \(x = A = 1\) hoăc 0,1 (bấm CALC
\(x = A = 1\) hoăc 0,1 (bấm CALC ![]() \(\rightarrow A\) ) cho kết quả khác 0 ta loại ngay đáp án đó
\(\rightarrow A\) ) cho kết quả khác 0 ta loại ngay đáp án đó ![]() \(\Rightarrow\) Loại A
\(\Rightarrow\) Loại A
Thay ![]() \(F_{i}(x)\) bởi đáp án B và gán A như trên ta nhận kết quả khác
\(F_{i}(x)\) bởi đáp án B và gán A như trên ta nhận kết quả khác ![]() \(0
\Rightarrow\) Loại B
\(0
\Rightarrow\) Loại B
Thay ![]() \(F_{i}(x)\) bởi đáp án C và gán A như trên ta nhận kết quả bằng 0 ; chắc ăn kiểm tra thêm vài giá trị của A như
\(F_{i}(x)\) bởi đáp án C và gán A như trên ta nhận kết quả bằng 0 ; chắc ăn kiểm tra thêm vài giá trị của A như ![]() \(0;0,2;0,5,1\)
\(0;0,2;0,5,1\)
![]() \(\Rightarrow\) Chọn
\(\Rightarrow\) Chọn ![]() \(C\). (Không nên gán
\(C\). (Không nên gán ![]() \(x = A\) giá trị quá lớn máy sẽ chũi đấy)
\(x = A\) giá trị quá lớn máy sẽ chũi đấy)
Ví dụ: ![]() \(\int_{}^{}\ x\sin x \cos xdx\) bằng
\(\int_{}^{}\ x\sin x \cos xdx\) bằng
A. ![]() \(\frac{1}{2}\left( \frac{1}{4}\sin2x -
\frac{x}{2}\cos2x \right) + C\) B.
\(\frac{1}{2}\left( \frac{1}{4}\sin2x -
\frac{x}{2}\cos2x \right) + C\) B. ![]() \(- \frac{1}{2}\left( \frac{1}{2}\sin2x -
\frac{x}{4}\cos2x \right) + C\)
\(- \frac{1}{2}\left( \frac{1}{2}\sin2x -
\frac{x}{4}\cos2x \right) + C\)
C. ![]() \(\frac{1}{2}\left( \frac{1}{4}\sin2x +
\frac{x}{2}\cos2x \right) + C\) D.
\(\frac{1}{2}\left( \frac{1}{4}\sin2x +
\frac{x}{2}\cos2x \right) + C\) D. ![]() \(- \frac{1}{2}\left( \frac{1}{2}\sin2x +
\frac{x}{4}\cos2x \right) + C\)
\(- \frac{1}{2}\left( \frac{1}{2}\sin2x +
\frac{x}{4}\cos2x \right) + C\)
Hướng dẫn giải
Ta có:
![]() \(A\sin A\cos A - \left. \ \frac{d}{dx}\left(
\frac{1}{8}\sin2x - \frac{x}{4}\cos2x \right) \right|_{x = A}\)
\(A\sin A\cos A - \left. \ \frac{d}{dx}\left(
\frac{1}{8}\sin2x - \frac{x}{4}\cos2x \right) \right|_{x = A}\)
Gán ![]() \(A = 0,1\)
\(A = 0,1\)
Cho kết quả bằng 0 - kiểm tra vài giá trị khác như 0,![]() \(2;0,3;0,5\) ta nhận kết quả đều bằng 0
\(2;0,3;0,5\) ta nhận kết quả đều bằng 0 ![]() \(\Rightarrow\) Chọn A .
\(\Rightarrow\) Chọn A .
Ví dụ: ![]() \(\int\frac{- 2}{x(1 +\ln x)^{2}}dx(x > 0)\) bằng.
\(\int\frac{- 2}{x(1 +\ln x)^{2}}dx(x > 0)\) bằng.
A. ![]() \(F(x) = \frac{1 + \ln x}{1 - \ln x} +
C\) B.
\(F(x) = \frac{1 + \ln x}{1 - \ln x} +
C\) B. ![]() \(F(x) = \frac{1 - \ln x}{1 + \ln x} +
C\)
\(F(x) = \frac{1 - \ln x}{1 + \ln x} +
C\)
C. ![]() \(F(x) = \frac{\ln x - 1}{1 + \ln x} +
C\) D.
\(F(x) = \frac{\ln x - 1}{1 + \ln x} +
C\) D. ![]() \(- \frac{1}{2}\)
\(- \frac{1}{2}\)
Hướng dẫn giải
Ta có:
 \(\frac{- 2}{A(1 + \ln A)^{2}} - \left. \
\frac{d}{dx}\left( \frac{1 + \ln x}{1 - \ln x} \right) \right|_{x =
A}\) gán
\(\frac{- 2}{A(1 + \ln A)^{2}} - \left. \
\frac{d}{dx}\left( \frac{1 + \ln x}{1 - \ln x} \right) \right|_{x =
A}\) gán ![]() \(A = 0,1\) nhận kết quả khác
\(A = 0,1\) nhận kết quả khác ![]() \(0 \Rightarrow\) loai đáp án A
\(0 \Rightarrow\) loai đáp án A
Dạng 2: Tìm một nguyên hàm F(x) của hàm số f(x) biết F(x0) = M
Cú pháp:  \({F_i}\left( A \right) - M - \int_{{x_0}}^A {f\left( x \right)dx}\)
\({F_i}\left( A \right) - M - \int_{{x_0}}^A {f\left( x \right)dx}\)
Vi dụ: Tìm nguyên hàm ![]() \(F(x)\) của hàm số
\(F(x)\) của hàm số ![]() \(f(x) = \frac{x^{3} + 3x^{2} + 3x - 1}{x^{2}
+ 2x + 1}\) , biết
\(f(x) = \frac{x^{3} + 3x^{2} + 3x - 1}{x^{2}
+ 2x + 1}\) , biết ![]() \(F(l) =
\frac{1}{3}\) .
\(F(l) =
\frac{1}{3}\) .
A. ![]() \(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1} - \frac{6}{13}\) B.
\(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1} - \frac{6}{13}\) B. ![]() \(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1}\)
\(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1}\)
C. ![]() \(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1} + \frac{13}{6}\) D.
\(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1} + \frac{13}{6}\) D. ![]() \(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1} - \frac{13}{6}\)
\(F(x) = \frac{x^{2}}{2} + x + \frac{2}{x +
1} - \frac{13}{6}\)
Hướng dẫn giải
Thực hiện giải toán như sau:
![]() \(\frac{A^{2}}{2} + A + \frac{2}{A + 1} -
\frac{6}{13} - \int_{1}^{A}\mspace{2mu}\frac{x^{3} + 3x^{2} + 3x -
1}{x^{2} + 2x + 1}\) gán
\(\frac{A^{2}}{2} + A + \frac{2}{A + 1} -
\frac{6}{13} - \int_{1}^{A}\mspace{2mu}\frac{x^{3} + 3x^{2} + 3x -
1}{x^{2} + 2x + 1}\) gán ![]() \(A =
0,1;1\) đều nhận kết quả khác
\(A =
0,1;1\) đều nhận kết quả khác ![]() \(0
\Rightarrow\) loai đáp án A
\(0
\Rightarrow\) loai đáp án A
![]() \(\frac{A^{2}}{2} + A + \frac{2}{A + 1} -
\frac{13}{6} - \int_{1}^{A}\mspace{2mu}\frac{x^{3} + 3x^{2} + 3x -
1}{x^{2} + 2x + 1}\) gán
\(\frac{A^{2}}{2} + A + \frac{2}{A + 1} -
\frac{13}{6} - \int_{1}^{A}\mspace{2mu}\frac{x^{3} + 3x^{2} + 3x -
1}{x^{2} + 2x + 1}\) gán ![]() \(A =
0,1;1\) nhận kết quả 0, kiểm tra thêm
\(A =
0,1;1\) nhận kết quả 0, kiểm tra thêm ![]() \(\Rightarrow\) Chọn D.
\(\Rightarrow\) Chọn D.
Vi dụ: Tìm 1 nguyên hàm ![]() \(F(x)\) của hàm số
\(F(x)\) của hàm số ![]() \(f(x) = \frac{5}{5\sin x + 3\cos x +
3}\), thỏa mãn
\(f(x) = \frac{5}{5\sin x + 3\cos x +
3}\), thỏa mãn ![]() \(F\left( \frac{\pi}{2}
\right) = 3\ln2\).
\(F\left( \frac{\pi}{2}
\right) = 3\ln2\).
A. ![]() \(F(x) = 3\ln\left| 5\tan\frac{x}{2} - 3
\right|\) B.
\(F(x) = 3\ln\left| 5\tan\frac{x}{2} - 3
\right|\) B. ![]() \(F(x) = \ln\left| 5\tan\frac{x}{2} + 3
\right|\)
\(F(x) = \ln\left| 5\tan\frac{x}{2} + 3
\right|\)
C. ![]() \(F(x) = \ln\left| 5\tan\frac{x}{2} - 3
\right| + 2ln2\) D.
\(F(x) = \ln\left| 5\tan\frac{x}{2} - 3
\right| + 2ln2\) D. ![]() \(F(x) = 3\ln\left| 5\tan\frac{x}{2} + 3
\right|\)
\(F(x) = 3\ln\left| 5\tan\frac{x}{2} + 3
\right|\)
Hướng dẫn giải
 \(3\ln\left| 5\tan\frac{A}{2} - 3 \right| -
3\ln2 - \int_{\frac{\pi}{2}}^{4}\mspace{2mu}\frac{5}{5\sin x + 3\cos x +
3}dx\) gán
\(3\ln\left| 5\tan\frac{A}{2} - 3 \right| -
3\ln2 - \int_{\frac{\pi}{2}}^{4}\mspace{2mu}\frac{5}{5\sin x + 3\cos x +
3}dx\) gán ![]() \(A = 0;0,1\) nhận kết quả khác
\(A = 0;0,1\) nhận kết quả khác ![]() \(0 \Rightarrow\) loại đáp án A
\(0 \Rightarrow\) loại đáp án A
 \(\ln\left| 5\tan\frac{A}{2} - 3 \right| -
3\ln2 - \int_{\frac{\pi}{2}}^{A}\mspace{2mu}\frac{5}{5\sin x + 3\cos x +
3}dx\) gán
\(\ln\left| 5\tan\frac{A}{2} - 3 \right| -
3\ln2 - \int_{\frac{\pi}{2}}^{A}\mspace{2mu}\frac{5}{5\sin x + 3\cos x +
3}dx\) gán ![]() \(A = 0;0,1;2\) nhận kết quả 0
\(A = 0;0,1;2\) nhận kết quả 0![]() \(\Rightarrow\) Chọn đáp án B
\(\Rightarrow\) Chọn đáp án B
Dạng 3: Tính tích phân  \(\int_a^b {f\left( x \right)dx}\) (Trong đó các đáp án đều là số vô tỉ: dạng căn, số e, số π các em nên bấm máy ghi nhận lại các kết quả trên).
\(\int_a^b {f\left( x \right)dx}\) (Trong đó các đáp án đều là số vô tỉ: dạng căn, số e, số π các em nên bấm máy ghi nhận lại các kết quả trên).
Cú pháp:  \(\int_a^b {f\left( x \right)dx}\)
\(\int_a^b {f\left( x \right)dx}\)
Ví dụ: ![]() \(\int_{1}^{e}\mspace{2mu}
x^{2}lnxdx\) bằng
\(\int_{1}^{e}\mspace{2mu}
x^{2}lnxdx\) bằng
A. ![]() \(\frac{e^{2} + 1}{4}\) B.
\(\frac{e^{2} + 1}{4}\) B. ![]() \(\frac{2e^{3} + 1}{9}\) C.
\(\frac{2e^{3} + 1}{9}\) C. ![]() \(\frac{3e^{3} + 2}{8}\) D.
\(\frac{3e^{3} + 2}{8}\) D. ![]() \(\frac{2e^{2} + 3}{3}\)
\(\frac{2e^{2} + 3}{3}\)
Hướng dẫn giải
![]() \(\frac{e^{2} + 1}{4} \approx
2,097264025\) -
\(\frac{e^{2} + 1}{4} \approx
2,097264025\) - ![]() \(\frac{2e^{3} + 1}{9}
\approx 4,574563716\) -
\(\frac{2e^{3} + 1}{9}
\approx 4,574563716\) - ![]() \(\frac{3e^{3}
+ 2}{8}7,782076346\)
\(\frac{3e^{3}
+ 2}{8}7,782076346\) ![]() \(\frac{2e^{2} +
3}{3} \approx 5,926037399\)
\(\frac{2e^{2} +
3}{3} \approx 5,926037399\)
Ví dụ:  \(\int_{0}^{\frac{\pi}{2}}\mspace{2mu}\frac{\sin2x}{\sqrt{\cos^{2}x
+ 4\sin^{2}x}}dx\) bằng
\(\int_{0}^{\frac{\pi}{2}}\mspace{2mu}\frac{\sin2x}{\sqrt{\cos^{2}x
+ 4\sin^{2}x}}dx\) bằng
A. ![]() \(\frac{3}{2}\) B.
\(\frac{3}{2}\) B. ![]() \(\frac{3}{4}\) C.
\(\frac{3}{4}\) C. ![]() \(\frac{2}{3} \approx
0,666666667\) D.
\(\frac{2}{3} \approx
0,666666667\) D. ![]() \(\frac{2}{5}\)
\(\frac{2}{5}\)
Ví dụ:  \(I =
\int_{0}^{\frac{\pi}{4}}\mspace{2mu}\frac{\sin\left( x - \frac{\pi}{4}
\right)dx}{\sin2x + 2(1 + \sin x + \cos x)}\).
\(I =
\int_{0}^{\frac{\pi}{4}}\mspace{2mu}\frac{\sin\left( x - \frac{\pi}{4}
\right)dx}{\sin2x + 2(1 + \sin x + \cos x)}\).
A. ![]() \(\frac{4 - 3\sqrt{2}}{4} \approx -
0,060660172\) B.
\(\frac{4 - 3\sqrt{2}}{4} \approx -
0,060660172\) B. ![]() \(\frac{4 + 3\sqrt{2}}{4}\)
\(\frac{4 + 3\sqrt{2}}{4}\)
C. ![]() \(\frac{4 + 3\sqrt{2}}{3}\) D.
\(\frac{4 + 3\sqrt{2}}{3}\) D. ![]() \(\frac{4 - 3\sqrt{2}}{3}\)
\(\frac{4 - 3\sqrt{2}}{3}\)
Ví dụ 10:  \(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\mspace{2mu}\frac{dx}{\sin^{2}x\sqrt{\cot x}}\)
\(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\mspace{2mu}\frac{dx}{\sin^{2}x\sqrt{\cot x}}\)
A. ![]() \(2(\sqrt[4]{3} - 1)\) B.
\(2(\sqrt[4]{3} - 1)\) B. ![]() \(2(\sqrt[4]{3} + 1)\) C.
\(2(\sqrt[4]{3} + 1)\) C. ![]() \(\sqrt[4]{3} - 1\) D.
\(\sqrt[4]{3} - 1\) D. ![]() \(\sqrt[4]{3} + 1\)
\(\sqrt[4]{3} + 1\)
Dạng 4: Tính diện tích hình phẳng - Thể tích khối tròn xoay
Ví dụ: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số ![]() \(y = (e + 1)x,y = \left( 1 + e^{x}
\right)x\) là
\(y = (e + 1)x,y = \left( 1 + e^{x}
\right)x\) là
A. ![]() \(e + \frac{1}{2}\) B.
\(e + \frac{1}{2}\) B. ![]() \(\frac{e}{2} + 1\) C.
\(\frac{e}{2} + 1\) C. ![]() \(e - \frac{1}{2}\) D.
\(e - \frac{1}{2}\) D. ![]() \(\frac{e}{2} - 1\)
\(\frac{e}{2} - 1\)
Hướng dẫn giải
Phương trình HĐGĐ ![]() \(f_{1}(x) - f_{2}(x) = 0
\Leftrightarrow x\left( e^{x} - e \right) = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = 1 \\
\end{matrix} \right.\)
\(f_{1}(x) - f_{2}(x) = 0
\Leftrightarrow x\left( e^{x} - e \right) = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = 1 \\
\end{matrix} \right.\)
![]() \(S = \int_{0}^{1}\mspace{2mu}\left|
x\left( e^{x} - e \right) \right|dx = \frac{e}{2} - 1 \approx
0,359140914\)
\(S = \int_{0}^{1}\mspace{2mu}\left|
x\left( e^{x} - e \right) \right|dx = \frac{e}{2} - 1 \approx
0,359140914\)
Ví dụ: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số ![]() \(y = \left| x^{2} - 4x + 3 \right|,y = x +
3\) là
\(y = \left| x^{2} - 4x + 3 \right|,y = x +
3\) là
A. ![]() \(\frac{6}{109}\) B.
\(\frac{6}{109}\) B. ![]() \(\frac{109}{6}\) C.
\(\frac{109}{6}\) C. ![]() \(\frac{13}{6}\) D.
\(\frac{13}{6}\) D. ![]() \(\frac{26}{3}\)
\(\frac{26}{3}\)
Hướng dẫn giải
Phương trình HĐGĐ ![]() \(f_{1}(x) - f_{2}(x) = 0
\Leftrightarrow \left| x^{2} - 4x + 3 \right| = x + 3 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = 5 \\
\end{matrix} \right.\)
\(f_{1}(x) - f_{2}(x) = 0
\Leftrightarrow \left| x^{2} - 4x + 3 \right| = x + 3 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = 5 \\
\end{matrix} \right.\)
![]() \(\cdot S =
\int_{0}^{5}\mspace{2mu}||x^{2} - 4x + 3| - (x + 3)|dx = \frac{109}{6}
\approx 18,16666667\)
\(\cdot S =
\int_{0}^{5}\mspace{2mu}||x^{2} - 4x + 3| - (x + 3)|dx = \frac{109}{6}
\approx 18,16666667\)
Ví dụ: Tính diện tích hình phẳng giới hạn bởi các đường: ![]() \(y = \sqrt{4 - \frac{x^{2}}{4}}\) và
\(y = \sqrt{4 - \frac{x^{2}}{4}}\) và ![]() \(y = \frac{x^{2}}{4\sqrt{2}}\) .
\(y = \frac{x^{2}}{4\sqrt{2}}\) .
A. ![]() \(2\pi - \frac{4}{3}\) B.
\(2\pi - \frac{4}{3}\) B. ![]() \(2\pi + \frac{3}{4}\) C.
\(2\pi + \frac{3}{4}\) C. ![]() \(2\pi + \frac{4}{3}\) D.
\(2\pi + \frac{4}{3}\) D. ![]() \(\pi + \frac{4}{3}\)
\(\pi + \frac{4}{3}\)
Hướng dẫn giải
Phương trình HĐGĐ
 \(f_{1}(x) - f_{2}(x) = 0
\Leftrightarrow \sqrt{4 - \frac{x^{2}}{4}} = \frac{x^{2}}{4\sqrt{2}}\)
\(f_{1}(x) - f_{2}(x) = 0
\Leftrightarrow \sqrt{4 - \frac{x^{2}}{4}} = \frac{x^{2}}{4\sqrt{2}}\)
![]() \(\Leftrightarrow \frac{x^{4}}{32} + \frac{x^{2}}{4} - 4 = 0
\Leftrightarrow x = \pm \sqrt{8}\)
\(\Leftrightarrow \frac{x^{4}}{32} + \frac{x^{2}}{4} - 4 = 0
\Leftrightarrow x = \pm \sqrt{8}\)
 \(\cdot S = \int_{-
\sqrt{8}}^{\sqrt{8}}\mspace{2mu}\left| \sqrt{4 - \frac{x^{2}}{4}} -
\frac{x^{2}}{4\sqrt{2}} \right|dx = 2\pi + \frac{4}{3} \approx
7,616518641\)
\(\cdot S = \int_{-
\sqrt{8}}^{\sqrt{8}}\mspace{2mu}\left| \sqrt{4 - \frac{x^{2}}{4}} -
\frac{x^{2}}{4\sqrt{2}} \right|dx = 2\pi + \frac{4}{3} \approx
7,616518641\)
Ví dụ. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số ![]() \(y = 1 - \sqrt{1 - x^{2}},y = x^{2}\) là
\(y = 1 - \sqrt{1 - x^{2}},y = x^{2}\) là
A. ![]() \(\frac{2}{3} -
\frac{\pi}{2}\) B.
\(\frac{2}{3} -
\frac{\pi}{2}\) B. ![]() \(\frac{4}{3} -
\frac{\pi}{2}\) C.
\(\frac{4}{3} -
\frac{\pi}{2}\) C. ![]() \(\frac{\pi}{2} -
\frac{4}{3}\) D.
\(\frac{\pi}{2} -
\frac{4}{3}\) D. ![]() \(\frac{\pi}{2} -
\frac{2}{3}\)
\(\frac{\pi}{2} -
\frac{2}{3}\)
Hướng dẫn giải
Phương trình HĐGĐ: ![]() \(f_{1}(x) = f_{2}(x)
\Leftrightarrow 1 - \sqrt{1 - x^{2}} = x^{2} \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = \pm 1 \\
\end{matrix} \right.\)
\(f_{1}(x) = f_{2}(x)
\Leftrightarrow 1 - \sqrt{1 - x^{2}} = x^{2} \Leftrightarrow
\left\lbrack \begin{matrix}
x = 0 \\
x = \pm 1 \\
\end{matrix} \right.\)
![]() \(S = \int_{- 1}^{1}\mspace{2mu}\left| 1 -
\sqrt{1 - x^{2}} - x^{2} \right|dx = 0,237462993\) chọn C
\(S = \int_{- 1}^{1}\mspace{2mu}\left| 1 -
\sqrt{1 - x^{2}} - x^{2} \right|dx = 0,237462993\) chọn C ![]() \(\ \left( \frac{\pi}{2} - \frac{4}{3} \approx
0,237462993 \right)\)
\(\ \left( \frac{\pi}{2} - \frac{4}{3} \approx
0,237462993 \right)\)
Ví dụ. Một cái lu có bán kính ở 2 đầu là ![]() \(2(dm)\) và ở giữa là
\(2(dm)\) và ở giữa là ![]() \(4(dm)\), chiều cao của cái lu là
\(4(dm)\), chiều cao của cái lu là ![]() \(8(dm)\). Tính lượng nước tối đa mà lu có thể chứa được.
\(8(dm)\). Tính lượng nước tối đa mà lu có thể chứa được.
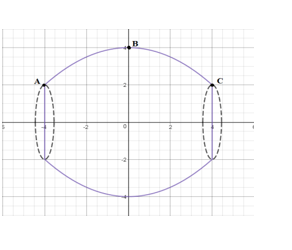
Phân tích:
Cái lu có dạng khối tròn xoay với đường sinh hình Parabol là đồ thị của hàm số ![]() \(y = ax^{2} + bx + c(a \neq
0)\). Do đó ta có thể áp dụng công thức tích phân để tính thể tích khố tròn xoay trên.
\(y = ax^{2} + bx + c(a \neq
0)\). Do đó ta có thể áp dụng công thức tích phân để tính thể tích khố tròn xoay trên.
Dựa vào kích thước của cái lu trên đề bài ta có thể xây dựng hệ trục tọa độ ![]() \(Oxy\) phù hợp và đơn giản như hình vẽ. Khi đó ta có thể sử dụng công thức tích phân để tính thể tích
\(Oxy\) phù hợp và đơn giản như hình vẽ. Khi đó ta có thể sử dụng công thức tích phân để tính thể tích
Từ chiều cao của cái lu ta tìm được cận của tích phân
Từ đồ dài bán kính 2 đầu và ở giữa ta lấy được 3 điểm ![]() \(A( - 4;2)\);
\(A( - 4;2)\); ![]() \(B(0;4)\);
\(B(0;4)\); ![]() \(C(4;2)\)thuộc đồ thị
\(C(4;2)\)thuộc đồ thị ![]() \((P)\)
\((P)\)
Hướng dẫn giải:
Tìm phương trình Parabol ![]() \((P):y = ax^{2} +
bx + c(a \neq 0)\) qua 3 điểm
\((P):y = ax^{2} +
bx + c(a \neq 0)\) qua 3 điểm ![]() \(A( -
4;2)\);
\(A( -
4;2)\); ![]() \(B(0;4)\);
\(B(0;4)\); ![]() \(C(4;2)\)
\(C(4;2)\)
Giải hệ phương trình:
 \(\left\{ \begin{matrix}
16a - 4b + c = 2 \\
c = 4 \\
16a + 4b + c = 2
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
a = \frac{- 1}{8} \\
b = 0 \\
c = 4
\end{matrix} \right.\ \Rightarrow (P):y = \frac{- 1}{8}x^{2} +
4\)
\(\left\{ \begin{matrix}
16a - 4b + c = 2 \\
c = 4 \\
16a + 4b + c = 2
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
a = \frac{- 1}{8} \\
b = 0 \\
c = 4
\end{matrix} \right.\ \Rightarrow (P):y = \frac{- 1}{8}x^{2} +
4\)
Như vậy: ![]() \(V = \pi\int_{- 4}^{4}{\left(
\frac{- 1}{8}x^{2} + 4 \right)^{2}dx}\)
\(V = \pi\int_{- 4}^{4}{\left(
\frac{- 1}{8}x^{2} + 4 \right)^{2}dx}\)
Sử dụng máy tính CASIO fx-580VN X tính tích phân trên
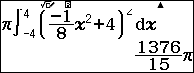
Vậy thể tích cái lu là: ![]() \(V =
\frac{1376\pi}{15} \approx 288.189\left( dm^{2} \right)\)
\(V =
\frac{1376\pi}{15} \approx 288.189\left( dm^{2} \right)\)
Ví dụ: Tính thể tích cái bình hoa với kích thước như hình vẽ biết bình cao ![]() \(2\pi(cm)\) và đường sinh của bình khi nằm ngang là đường cong có dạng
\(2\pi(cm)\) và đường sinh của bình khi nằm ngang là đường cong có dạng ![]() \(y =\sin x + 2\)?
\(y =\sin x + 2\)?
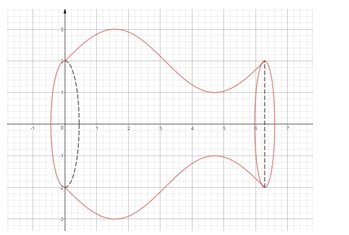
Phân tích:
Cái bình có dạng khối tròn xoay với đường sinh hình Parabol là đồ thị của hàm số![]() \(y = sinx + 2\). Do đó ta có thể áp dụng công thức tích phân để tính thể tích khố tròn xoay trên.
\(y = sinx + 2\). Do đó ta có thể áp dụng công thức tích phân để tính thể tích khố tròn xoay trên.
Để việc tính toán trở nên thuận lợi ta nên xây dựng hệ trục tọa độ ![]() \(Oxy\) cho bình nằm ngang và trục
\(Oxy\) cho bình nằm ngang và trục ![]() \(Ox\) chia bình thành hai phần bằng nhau
\(Ox\) chia bình thành hai phần bằng nhau
Hướng dẫn giải
Xây dựng hệ trục tọa độ như hình vẽ:
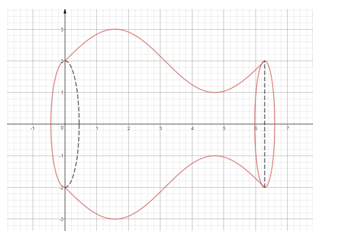
Khi đó thể tích của bình bằng: ![]() \(V =\pi\int_{0}^{2\pi}(\sin x + 2)^{2}dx\)
\(V =\pi\int_{0}^{2\pi}(\sin x + 2)^{2}dx\)
Sử dụng máy tính CASIO fx- 580VN X tính tích phân ![]() \(\int_{0}^{2\pi}(\sin x + 2)^{2}dx\)
\(\int_{0}^{2\pi}(\sin x + 2)^{2}dx\)

(Trước khi thực hiện phép tính cần chuyển máy về chế độ Radian)
Vậy thể tích bình hoa ![]() \(V =
9\pi^{2}(cm^{3})\).
\(V =
9\pi^{2}(cm^{3})\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
----------------------------------------
Trên đây VnDoc.com vừa giới thiệu tới các bạn Tính nhanh nguyên hàm - tích phân bằng máy tính Casio. Bài viết tổng hợp các cách tính nhanh nguyên hàm và tích phân bằng máy tính Casio, cách sử dụng máy tính Casio cùng với những ví dụ kèm theo. Mong rằng qua bài viết này các bạn có thể học tập tốt hơn nhé. Mời bạn đọc cùng tham khảo thêm mục Thi THPT Quốc gia 2025.