Cách tìm hình chiếu của điểm lên đường thẳng và mặt phẳng
Tìm tọa độ hình chiếu của điểm lên đường thẳng và mặt phẳng
Trong hình học không gian, hình chiếu của điểm lên đường thẳng và mặt phẳng là một khái niệm cơ bản nhưng rất quan trọng, đặc biệt trong việc xác định khoảng cách, tính góc hoặc giải các bài toán hình học phức tạp. Việc nắm vững phương pháp tìm hình chiếu giúp học sinh giải nhanh và chính xác nhiều dạng bài trong chương trình Toán lớp 12 và các kỳ thi lớn. Bài viết dưới đây sẽ hướng dẫn bạn cách tìm hình chiếu của điểm lên đường thẳng và mặt phẳng, đi kèm công thức, phương pháp hình học – đại số, và ví dụ minh họa cụ thể.
1. Thế nào là hình chiếu của một điểm lên đường thẳng, mặt phẳng?
Định nghĩa 1: Trong không gian, cho điểm 
\(M\) và đường thẳng \(d\).
- Nếu \(M \in d\) thì hình chiếu của \(M\) trên đường thẳng \(d\) là chính nó.
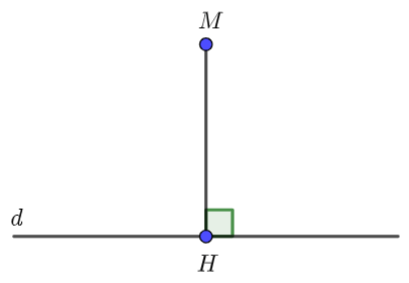
- Nếu \(M \notin d\) thì hình chiếu của \(M\) trên đường thẳng \(d\) là điểm \(H
\in d\) sao cho \(MH\bot d\)
Định nghĩa 2: Trong không gian, cho điểm \(M\) và mặt phẳng \((P)\).
- Nếu \(M \in (P)\) thì hình chiếu của \(M\) trên mặt phẳng \((P)\)là chính nó.
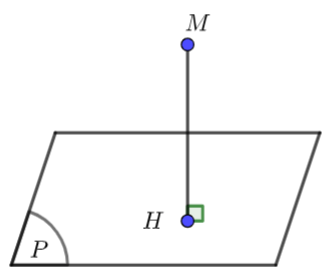
- Nếu \(M \notin (P)\) thì hình chiếu của \(M\) trên mặt phẳng \((P)\)là điểm \(H
\in (P)\) sao cho \(MH\bot(P)\).
2. Cách tìm tọa độ hình chiếu của điểm lên đường thẳng
Để tìm hình chiếu \(H\) của điểm \(M\) lên đường thẳng \(d\), ta làm theo một trong hai cách sau:
Cách 1:
- Bước 1: Do điểm \(H\) thuộc đường thẳng \(d\) nên tham số tọa độ điểm \(H\) theo tham số \(t\).
- Bước 2: Do \(MH\bot d\) nên \(\overrightarrow{MH}.\overrightarrow{u_{d}} =
0\), từ đó giải tìm \(t\).
- Bước 3: Thay \(t\) vào tọa độ điểm \(H\) đã tham số ở bước 1.
Cách 2:
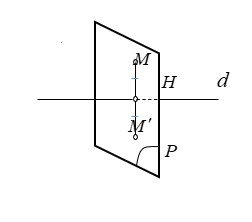
- Bước 1: Viết phương trình mặt phẳng \((P)\) qua \(M\) và vuông góc với \(d.\)
- Bước 2: Do điểm \(H\) thuộc đường thẳng \(d\) nên tham số tọa độ điểm \(H\) theo tham số \(t\).
- Bước 3: Thay tọa độ điểm \(H\) vào phương trình mặt phẳng \((P)\) rồi giải tìm \(t\).
- Bước 4: Thay \(t\) vào tọa độ điểm \(H\) đã tham số ở bước 1.
Đặc biệt: Điểm \(M(x_{M};y_{M};z_{M})\) có
- Hình chiếu trên trục \(Ox\) là \(M_{1}(x_{M};0;0)\).
- Hình chiếu trên trục \(Oy\) là \(M_{2}(0;y_{M};0)\).
- Hình chiếu trên trục \(Oz\) là \(M_{3}(0;0;z_{M})\).
3. Cách tìm tọa độ hình chiếu của điểm lên mặt phẳng
Để tìm hình chiếu \(H\) của điểm \(M\) trên mặt phẳng \((P)\), ta làm như sau:
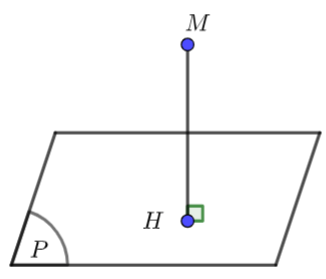
- Bước 1: Viết phương trình đường thẳng \(d\) qua \(M\) và vuông góc với mặt phẳng \(P\).
- Bước 2: Tìm tọa độ giao điểm \(H\) của đường thẳng \(d\) và mặt phẳng \((P)\).
Đặc biệt: Điểm \(M(x_{M};y_{M};z_{M})\) có
- Hình chiếu trên mặt phẳng\(Oxy\) là \(M_{1}(x_{M};y_{M};0)\).
- Hình chiếu trên trục \(Oyz\) là \(M_{2}(0;y_{M};z_{M})\).
- Hình chiếu trên trục \(Ozx\) là \(M_{3}(x_{M};0;z_{M})\).
4. Bài tập tìm tọa độ hình chiếu của điểm lên đường thẳng và mặt phẳng
Câu 1. Trong không gian Oxyz, tìm tọa độ hình chiếu vuông góc của điểm A(1; 2; 5) trên trục Ox?
Hướng dẫn giải
Hình chiếu vuông góc của điểm A(1;2;5) trên trục Ox có tọa độ là (1;0;0).
Câu 2. Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M(2\ ;\ - 2\
;\ 1)\) trên mặt phẳng \((Oxy)\) có tọa độ là
A.\((2\ ;\ 0\ ;\ 1)\). B.\((2\ ;\ - 2\ ;\ 0)\). C.\((0\ ;\ - 2\ ;\ 1)\). D.\((0\ ;\ 0\ ;\ 1)\).
Hướng dẫn giải
Ta có hình chiếu của điểm \(M\left( x_{0}\
;\ y_{0}\ ;\ z_{0} \right)\) trên mặt phẳng \((Oxy)\) là điểm \(M'\left( x_{0}\ ;\ y_{0}\ ;\ 0
\right)\).
Do đó hình chiếu của điểm \(M(2\ ;\ - 2\
;\ 1)\) trên mặt phẳng \((Oxy)\) là điểm \(M'(2\ ;\ - 2\ ;\
0)\).
Câu 3. Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M(2;\ 1;\ -
1)\) trên trục \(Oz\) có tọa độ là
A.\((2;\ 0;0)\). B.\((0;\ 1;\ 0)\). C.\((2;\ 1;\ 0)\). D.\((0;\ 0;\ - 1)\).
Hướng dẫn giải
Hình chiếu vuông góc của điểm \(M(2;\
1;\ - 1)\) trên trục \(Oz\) có tọa độ là: \((0;\ 0;\ - 1)\).
Câu 4. Trong không gian \(Oxyz\), tọa độ hình chiếu vuông góc của điểm \(A(3;2;
- 1)\) lên mặt phẳng \((\alpha):x + y +
z = 0\) là:
A.\(( - 2;1;1)\). B.\(\left( \frac{5}{3};\frac{2}{3}; - \frac{7}{3}
\right)\). C.\((1;1; - 2)\). D.\(\left( \frac{1}{2};\frac{1}{4};\frac{1}{4}
\right)\).
Hướng dẫn giải
Gọi \(H\) là hình chiếu của \(A(3;2; - 1)\) lên mặt phẳng \((\alpha):x + y + z = 0\). Khi đó: \(AH\) nhận \(\overrightarrow{n}(1;1;1)\) là vectơ chỉ phương suy ra phương trình \(AH:\frac{x -
3}{1} = \frac{y - 2}{1} = \frac{z + 1}{1}\).
Do \(H \in AH \Rightarrow H(3 + t;\ \ 2 +
t;\ - 1 + t)\).
Do \(H \in (\alpha) \Rightarrow 3 + t + 2 +
t - 1 + t = 0\)
\(\Leftrightarrow t = - \frac{4}{3}
\Rightarrow H\left( \frac{5}{3};\frac{2}{3}; - \frac{7}{3}
\right)\).
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho điểm \(M( - 4;0;0)\) và đường thẳng\(\Delta:\left\{ \begin{matrix}
x = 1 - t \\
y = - 2 + 3t \\
z = - 2t \\
\end{matrix} \right.\). Gọi \(H(a;b;c)\) là hình chiếu của \(M\) lên \(\Delta\). Tính a + b + c.
A.\(5\). B.\(- 1\). C.\(-
3\). D.\(7\).
Hướng dẫn giải
Gọi \(H\) là hình chiếu của \(M\) lên \(\Delta\)nên tọa độ của H có dạng \(H(1 - t; - 2 + 3t; - 2t)\) và \(\overrightarrow{MH}\bot\overrightarrow{u_{\Delta}}\)
\(\overrightarrow{MH}.\overrightarrow{u_{\Delta}} =
0 \Leftrightarrow 14t - 11 = 0 \Leftrightarrow t =
\frac{11}{14}\)
\(\Rightarrow
H(\frac{3}{14};\frac{5}{14};\frac{- 22}{14}) \Rightarrow a + b + c = -
1\)
--------------------------------------------------------
Như vậy, việc tìm hình chiếu của điểm lên đường thẳng hoặc mặt phẳng không chỉ là kỹ năng cần thiết trong học tập mà còn có nhiều ứng dụng thực tiễn. Hy vọng bài viết đã giúp bạn nắm được phương pháp giải bài toán nhanh và hiệu quả. Hãy ôn luyện thêm với các bài tập và ví dụ để làm chủ kiến thức này. Đừng quên chia sẻ bài viết nếu bạn thấy hữu ích nhé!
