Cách tìm GTLN, GTNN của hàm số bậc 3 dựa vào đồ thị hàm số
Cách đọc đồ thị hàm số bậc 3 để tìm GTLN, GTNN
Trong các đề ôn thi THPT Quốc gia môn Toán, dạng bài tìm GTLN, GTNN của hàm số bậc ba dựa vào đồ thị xuất hiện với tần suất cao và yêu cầu học sinh nhận diện nhanh giá trị đạt được của hàm số. Việc hiểu rõ mối quan hệ giữa hình dạng đồ thị và giá trị lớn nhất – nhỏ nhất giúp rút ngắn thời gian làm bài và nâng cao độ chính xác. Bài viết này hướng dẫn cách xác định hiệu quả thông qua quan sát trực quan.
Bài toán tổng quát:
Cho hàm số 
\(y = f(x) = ax^{3} + bx^{2} +
cx + d;(a \neq 0)\) xác định trên tập \(D.\) Xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số dựa vào đồ thị hàm số đã cho.
-
Số M gọi là giá trị lớn nhất của hàm số
\(y = f(x)\) trên \(D\) nếu: \(\left\{ \begin{matrix}
f(x) \leq M,\forall x \in D \\
\exists x_{0} \in D,f(x_{0}) = M
\end{matrix} \right.\). Kí hiệu: \(M
= \max_{x \in D}\ f(x)\). -
Số
\(m\) gọi là giá trị nhỏ nhất của hàm số \(y = f(x)\) trên \(D\) nếu: \(\left\{ \begin{matrix}
f(x) \geq m,\forall x \in D \\
\exists x_{0} \in D,f(x_{0}) = m
\end{matrix} \right.\). Kí hiệu: \(m
= \min_{x \in D}\ f(x)\).
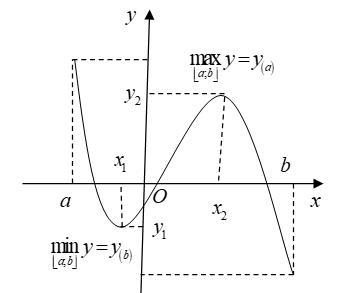
Hình vẽ minh họa xét trên đoạn \(\lbrack
a;\ b\rbrack\).
Ví dụ 1. Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\lbrack -
1;3\rbrack\) có đồ thị hàm số như hình vẽ bên.
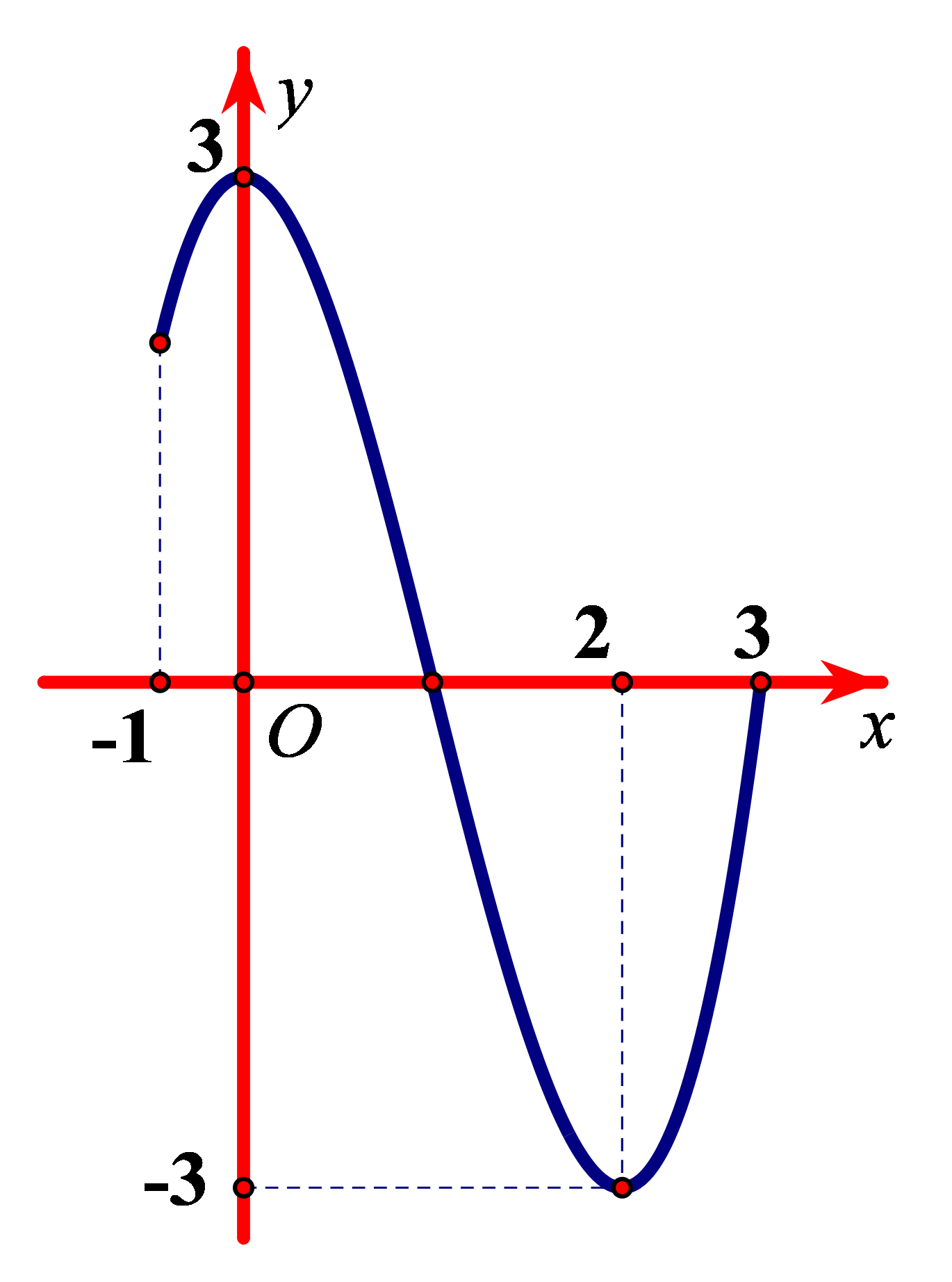
Mệnh đề nào sau đây đúng về hàm số đó?
A. Hàm số \(f(x)\) đạt giá trị lớn nhất tại \(x = 3\).
B. Hàm số \(f(x)\) đạt giá trị nhỏ nhất tại \(x = 2\).
C. Hàm số \(f(x)\) đạt cực tiểu tại \(x = - 1\).
D. Hàm số \(f(x)\) đồng biến trên khoảng \(( - 1;3)\).
Hướng dẫn giải
Chọn B
Dựa vào đồ thị, ta thấy hàm số \(f(x)\) đạt giá trị nhỏ nhất tại \(x = 2\).
Ví dụ 2. Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\lbrack -
5;3\rbrack\) có đồ thị hàm số như hình vẽ bên.
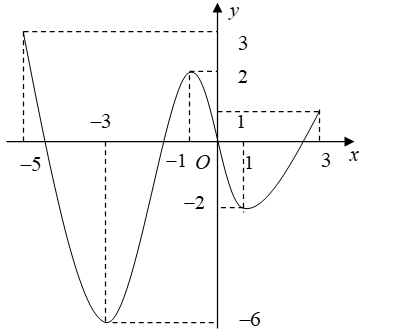
Mệnh đề nào sau đây sai?
A. Hàm số đạt giá trị lớn nhất bằng \(3\).
B. Hàm số đạt giá trị nhỏ nhất bằng \(-
6\).
C. Giá trị cực tiểu tại \(- 6\).
D. Hàm số đạt cực đại tại \(x = -
5\).
Hướng dẫn giải
Chọn D
Dựa vào đồ thị hàm số, ta thấy
Hàm số đạt cực đại tại \(x = - 5\) là sai. Sửa lại, Hàm số đạt cực đại tại \(x =
- 1\).
Ví dụ 3. Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên.
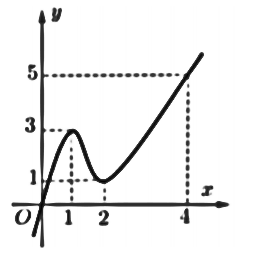
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( - \frac{3sinx}{2} + \frac{5}{2}
\right)\) bằng bao nhiêu?
A. \(5\). B. \(4\). C. \(6\). D. \(3\).
Hướng dẫn giải
Chọn C
Ta có \(1 \leq - \frac{3sinx}{2} +
\frac{5}{2} \leq 4\).
Đặt \(t = - \frac{3sinx}{2} + \frac{5}{2}
\Rightarrow t \in \lbrack 1;4\rbrack\), theo đồ thị ta có:
\(\max_{\lbrack 1;4\rbrack}f(t) = f(4) =
5,\min_{\lbrack 1;4\rbrack}f(t) = f(2) = 1\)
Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( - \frac{3sinx}{2} + \frac{5}{2}
\right)\) là \(5 + 1 = 6\).
--------------------------------------------
Thông qua việc luyện tập xác định GTLN, GTNN của hàm bậc ba từ đồ thị, học sinh sẽ hình thành kỹ năng đọc đồ thị nhanh và chính xác. Đây là nội dung quan trọng trong quá trình ôn thi THPT Quốc gia môn Toán, giúp xử lý tốt các câu hỏi trắc nghiệm liên quan đến hàm số.
