Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Cách xác định hệ số hàm bậc ba dựa vào đồ thị hàm số

Bài tập Toán 12 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách tìm hệ số a b c d của hàm bậc ba qua đồ thị

A. Dạng bài đọc đồ thị hàm bậc ba Toán 12
B. Ví dụ minh họa xác định hệ số hàm bậc ba

Trong các bài toán hàm số bậc ba Toán 12, dạng xác định hệ số của hàm số dựa vào đồ thị xuất hiện thường xuyên và đòi hỏi khả năng quan sát, phân tích đặc điểm hình học một cách chính xác. Việc nắm rõ mối liên hệ giữa đồ thị và các hệ số giúp học sinh xử lý nhanh các câu hỏi trắc nghiệm cũng như bài tập tự luận. Bài viết này hướng dẫn cách làm hiệu quả kèm bài tập minh họa có đáp án.

A. Dạng bài đọc đồ thị hàm bậc ba Toán 12

Áp dụng: Hàm số $y = ax^{3} + bx^{2} + cx + d$ $y = ax^{3} + bx^{2} + cx + d$ có 2 điểm cực trị.

Quy trình xác định:

* Xác định hệ số $a$:

Hướng đồ thị bên phải đi lên thì $a > 0$.
Hướng đồ thị bên phải đi xuống thì $a < 0$.

* Xác định hệ số $d$: Đồ thị cắt trục $Oy$ tại điểm $A(0;\ d)$ $A(0;\ d)$.

Điểm $A(0;\ d)$ $A(0;\ d)$ nằm phía trên trục $Ox$ thì $d > 0$.
Điểm $A(0;\ d)$ $A(0;\ d)$ nằm phía dưới trục $Ox$ thì $d < 0$.
Điểm $A(0;\ d)$ $A(0;\ d)$ trùng với gốc tọa độ thì $d = 0$.

* Xác định hệ số $c$: Đồ thị có hai điểm cực trị có hoành độ là $x_{1};\ x_{2}$ $x_{1};\ x_{2}$ với $x_{1};\ x_{2}$ $x_{1};\ x_{2}$ là nghiệm của phương trình $y' = 3ax^{2} + 2bx + c = 0$.

Nếu $x_{1};\ x_{2}$ $x_{1};\ x_{2}$ cùng dấu tức cùng phía so với trục $Oy$ thì $x_{1}.x_{2} = \frac{c}{3a} > 0$ $x_{1}.x_{2} = \frac{c}{3a} > 0$.
Nếu $x_{1};\ x_{2}$ $x_{1};\ x_{2}$ trái dấu tức khác phía so với trục $Oy$ thì $x_{1}.x_{2} = \frac{c}{3a} < 0$ $x_{1}.x_{2} = \frac{c}{3a} < 0$.
Nếu $x_{1} = 0$ $x_{1} = 0$ hoặc $x_{2} = 0$ $x_{2} = 0$ tức cực trị nằm trên trục $Oy$ thì $x_{1}.x_{2} = \frac{c}{3a} = 0 \Rightarrow c = 0$ $x_{1}.x_{2} = \frac{c}{3a} = 0 \Rightarrow c = 0$.

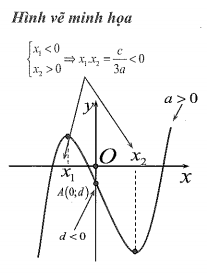* Xác định hệ số $b$: Đồ thị có hai điểm cực trị có hoành độ là $x_{1};\ x_{2}$ $x_{1};\ x_{2}$ với $x_{1};\ x_{2}$ $x_{1};\ x_{2}$ là nghiệm của phương trình $y' = 3ax^{2} + 2bx + c = 0$.

Nếu $x_{1} + x_{2} > 0 \Leftrightarrow - \frac{2b}{3a} > 0$ $x_{1} + x_{2} > 0 \Leftrightarrow - \frac{2b}{3a} > 0$.
Nếu $x_{1} + x_{2} < 0 \Leftrightarrow - \frac{2b}{3a} < 0$ $x_{1} + x_{2} < 0 \Leftrightarrow - \frac{2b}{3a} < 0$.
$x_{1} + x_{2} = 0 \Leftrightarrow - \frac{2b}{3a} = 0 \Rightarrow b = 0$ $x_{1} + x_{2} = 0 \Leftrightarrow - \frac{2b}{3a} = 0 \Rightarrow b = 0$.

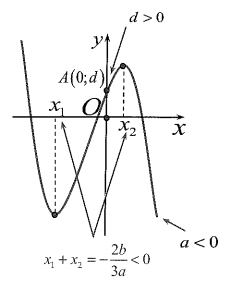B. Ví dụ minh họa xác định hệ số hàm bậc ba

Ví dụ 1. Cho hàm số $y = \ a\ x^{3} + 3x + d\ \ \ \left( a\ ,\ d\mathbb{\ \in \ R} \right)$ $y = \ a\ x^{3} + 3x + d\ \ \ \left( a\ ,\ d\mathbb{\ \in \ R} \right)$ có đồ thị như hình bên.

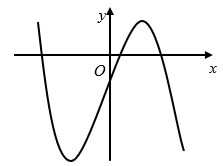
Mệnh đề nào dưới đây đúng?

A. $a\ > \ 0\ ;\ \ d\ > \ 0$ $a\ > \ 0\ ;\ \ d\ > \ 0$. B. $a\ < \ 0\ ;\ \ d\ > \ 0$ $a\ < \ 0\ ;\ \ d\ > \ 0$.

C. $a\ > \ 0\ ;\ \ d\ < \ 0$ $a\ > \ 0\ ;\ \ d\ < \ 0$. D. $a\ < \ 0\ ;\ \ d\ < \ 0$ $a\ < \ 0\ ;\ \ d\ < \ 0$.

Phân tích hướng dẫn giải

Đây là dạng toán xét dấu hệ số hàm số khi biết đồ thị hàm số và nhận dạng đồ thị hàm số.

⬥ Xác định hệ số $a$: Dựa vào hình dáng đồ thị hàm số bậc ba

+ $\lim_{x \rightarrow + \infty}y = + \infty \Rightarrow a > 0;\lim_{x \rightarrow + \infty}y = - \infty \Rightarrow a < 0$ $\lim_{x \rightarrow + \infty}y = + \infty \Rightarrow a > 0;\lim_{x \rightarrow + \infty}y = - \infty \Rightarrow a < 0$

⬥ Xác định hệ số $d$: Dựa vào vị trí giao điểm của đồ thị với trục tung.

Giao điểm của đồ thị với trục tung nằm trên trục hoành $\Rightarrow d\ > \ 0$ $\Rightarrow d\ > \ 0$.

Giao điểm của đồ thị với trục tung nằm dưới trục hoành $\Rightarrow d\ < \ 0$ $\Rightarrow d\ < \ 0$.

Hướng giải toán

B1: Dựa vào hình dáng của đồ thị để xác định dấu của hệ số $a$.

B2: Dựa vào giao điểm của đồ thị với trục tung để xác định dấu của hệ số $d$.

Giao điểm của đồ thị với trục tung nằm dưới trục hoành nên hệ số $d\ < \ 0$ $d\ < \ 0$.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn D

Dựa vào hình dáng đồ thị hàm số bậc ba, ta có hệ số $a\ < \ 0$ $a\ < \ 0$, loại đáp án A và C.

Giao điểm của đồ thị với trục tung nằm dưới trục hoành nên hệ số $d\ < \ 0$ $d\ < \ 0$, loại B.

Ví dụ 2. Hàm số $y = ax^{3} + bx^{2} + cx + d$ $y = ax^{3} + bx^{2} + cx + d$ có đồ thị như hình vẽ bên.

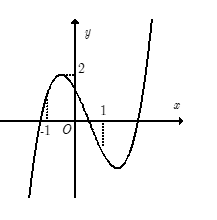
Mệnh đề nào sau đây là đúng?

A. $a > 0,\ b > 0,\ c < 0,\ d > 0$ $a > 0,\ b > 0,\ c < 0,\ d > 0$. B. $a < 0,\ b < 0,\ c < 0,\ d < 0$ $a < 0,\ b < 0,\ c < 0,\ d < 0$.

C. $a > 0,\ b < 0,\ c < 0,\ d > 0$ $a > 0,\ b < 0,\ c < 0,\ d > 0$. D. $a > 0,\ b > 0,\ c > 0,\ d < 0$ $a > 0,\ b > 0,\ c > 0,\ d < 0$.

Hướng dẫn giải

Chọn C

Đồ thị hàm số thể hiện $a > 0$; cắt trục tung tại điểm có tung độ dương nên $d > 0$.

Hàm số có $- 1 < x_{CD} < 0,\ x_{CT} > 1\overset{}{\rightarrow}\left\{ \begin{matrix} x_{CD} + x_{CT} > 0 \\ x_{CD}.x_{CT} < 0 \end{matrix} \right.$ $- 1 < x_{CD} < 0,\ x_{CT} > 1\overset{}{\rightarrow}\left\{ \begin{matrix} x_{CD} + x_{CT} > 0 \\ x_{CD}.x_{CT} < 0 \end{matrix} \right.$. $(*)$

Ta có $y' = 3ax^{2} + 2bx + c = 0.$ Do đó $(*) \leftrightarrow \left\{ \begin{matrix} - \frac{2b}{3a} > 0\overset{}{\rightarrow}\frac{b}{a} < 0\overset{a > 0}{\rightarrow}b < 0 \\ \frac{c}{3a} < 0\overset{}{\rightarrow}\frac{c}{a} < 0\overset{a > 0}{\rightarrow}c < 0 \end{matrix} \right.\ .$ $(*) \leftrightarrow \left\{ \begin{matrix} - \frac{2b}{3a} > 0\overset{}{\rightarrow}\frac{b}{a} < 0\overset{a > 0}{\rightarrow}b < 0 \\ \frac{c}{3a} < 0\overset{}{\rightarrow}\frac{c}{a} < 0\overset{a > 0}{\rightarrow}c < 0 \end{matrix} \right.\ .$

Vậy $a > 0,\ b < 0,\ c < 0,\ d > 0.$ $a > 0,\ b < 0,\ c < 0,\ d > 0.$

Ví dụ 3. Cho biết hàm số $y = ax^{3} + bx^{2} + cx + d$ $y = ax^{3} + bx^{2} + cx + d$ có đồ thị như hình vẽ bên.

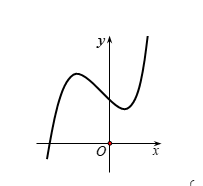
Trong các khẳng định sau, khẳng định nào đúng?

A. $\left\{ \begin{matrix} a > 0 \\ b^{2} - 3ac < 0 \end{matrix} \right.$ $\left\{ \begin{matrix} a > 0 \\ b^{2} - 3ac < 0 \end{matrix} \right.$. B. $\left\{ \begin{matrix} a < 0 \\ b^{2} - 3ac < 0 \end{matrix} \right.$ $\left\{ \begin{matrix} a < 0 \\ b^{2} - 3ac < 0 \end{matrix} \right.$.

C. $\left\{ \begin{matrix} a < 0 \\ b^{2} - 3ac > 0 \end{matrix} \right.$ $\left\{ \begin{matrix} a < 0 \\ b^{2} - 3ac > 0 \end{matrix} \right.$. D. $\left\{ \begin{matrix} a > 0 \\ b^{2} - 3ac > 0 \end{matrix} \right.$ $\left\{ \begin{matrix} a > 0 \\ b^{2} - 3ac > 0 \end{matrix} \right.$.

Hướng dẫn giải

Chọn D

Từ đồ thị ta thấy có $a > 0$ và có 2 cực trị

$\Rightarrow y$ $\Rightarrow y' = 3ax^{2} + 2bx + c = 0$ có hai nghiệm phân biệt hay $\Delta = 4b^{2} - 12ac > 0 \Leftrightarrow b^{2} - 3ac > 0.$ $\Delta = 4b^{2} - 12ac > 0 \Leftrightarrow b^{2} - 3ac > 0.$

-----------------------------------------

Thông qua việc rèn luyện xác định hệ số hàm bậc ba từ đồ thị, học sinh sẽ hiểu sâu hơn bản chất của hàm số và mối liên hệ giữa đại số với hình học. Đây là nội dung quan trọng giúp củng cố kiến thức Toán 12, hỗ trợ tốt cho kiểm tra định kỳ và ôn thi hiệu quả.

Tải về

Chọn file muốn tải về: