VnDoc.com

Chuyên đề Xác định cực trị của hàm số khi biết đồ thị của hàm số

Ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách xác định cực đại cực tiểu của hàm số dựa vào đồ thị

A. Cách xác định cực trị của hàm số dựa vào thị hàm số
B. Bài tập minh họa xác định cực trị hàm số khi biết đồ thị hàm số
C. Bài tập vận dụng tự rèn luyện có hướng dẫn chi tiết

Trong các đề ôn thi THPT Quốc gia môn Toán, dạng toán xác định cực trị của hàm số khi biết đồ thị luôn được đánh giá cao bởi tính trực quan và khả năng phân loại học sinh. Chỉ cần khai thác đúng đặc điểm của đồ thị, thí sinh có thể nhanh chóng nhận biết điểm cực đại, cực tiểu của hàm số mà không cần tính toán phức tạp. Chuyên đề này giúp hệ thống hóa phương pháp và bài tập trọng tâm, hỗ trợ học sinh làm chủ dạng toán cực trị qua đồ thị.

A. Cách xác định cực trị của hàm số dựa vào thị hàm số

Đồ thị đang đi lên sau đó đổi hướng đi xuống tại điểm $x_{o}$ $x_{o}$ thì hàm số đạt cực đại tại điểm $x_{o}$ $x_{o}$. Khi đó $f\left( x_{o} \right)$ $f\left( x_{o} \right)$ được gọi là giá trị cực đại của hàm số $f(x)$

Đồ thị đang đi xuống sau đó đổi hướng đi lên tại điểm $x_{o}$ $x_{o}$ thì hàm số đạt cực tiểu tại điểm $x_{o}$ $x_{o}$. Khi đó $f\left( x_{o} \right)$ $f\left( x_{o} \right)$ được gọi là giá trị cực t của hàm số $f(x)$

Các điểm cực đại, cực tiểu của hàm số được gọi chung là điểm cực trị của hàm số

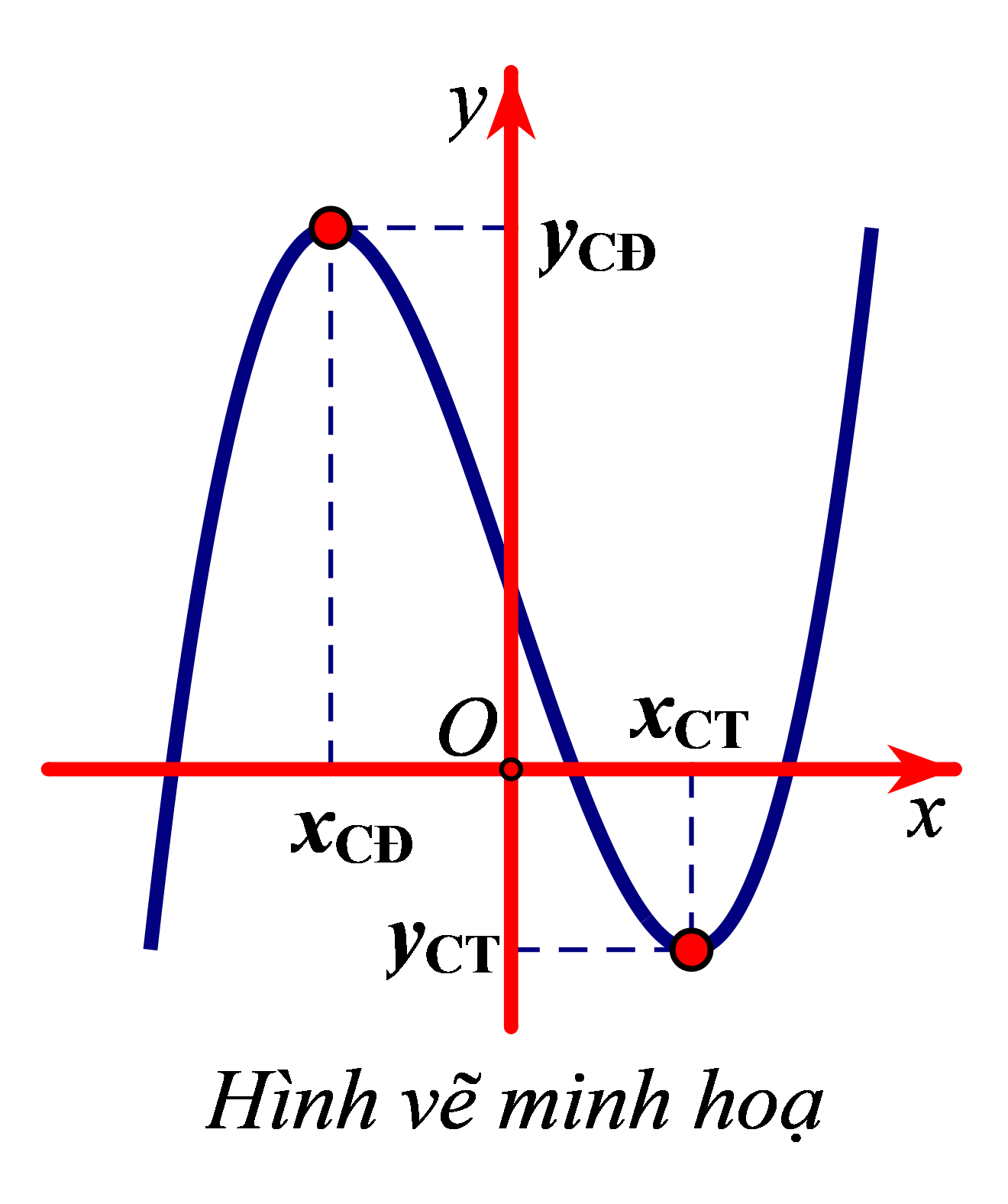B. Bài tập minh họa xác định cực trị hàm số khi biết đồ thị hàm số

Ví dụ 1. Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ $\mathbb{R}$ và có đồ thị là đường cong như hình vẽ.

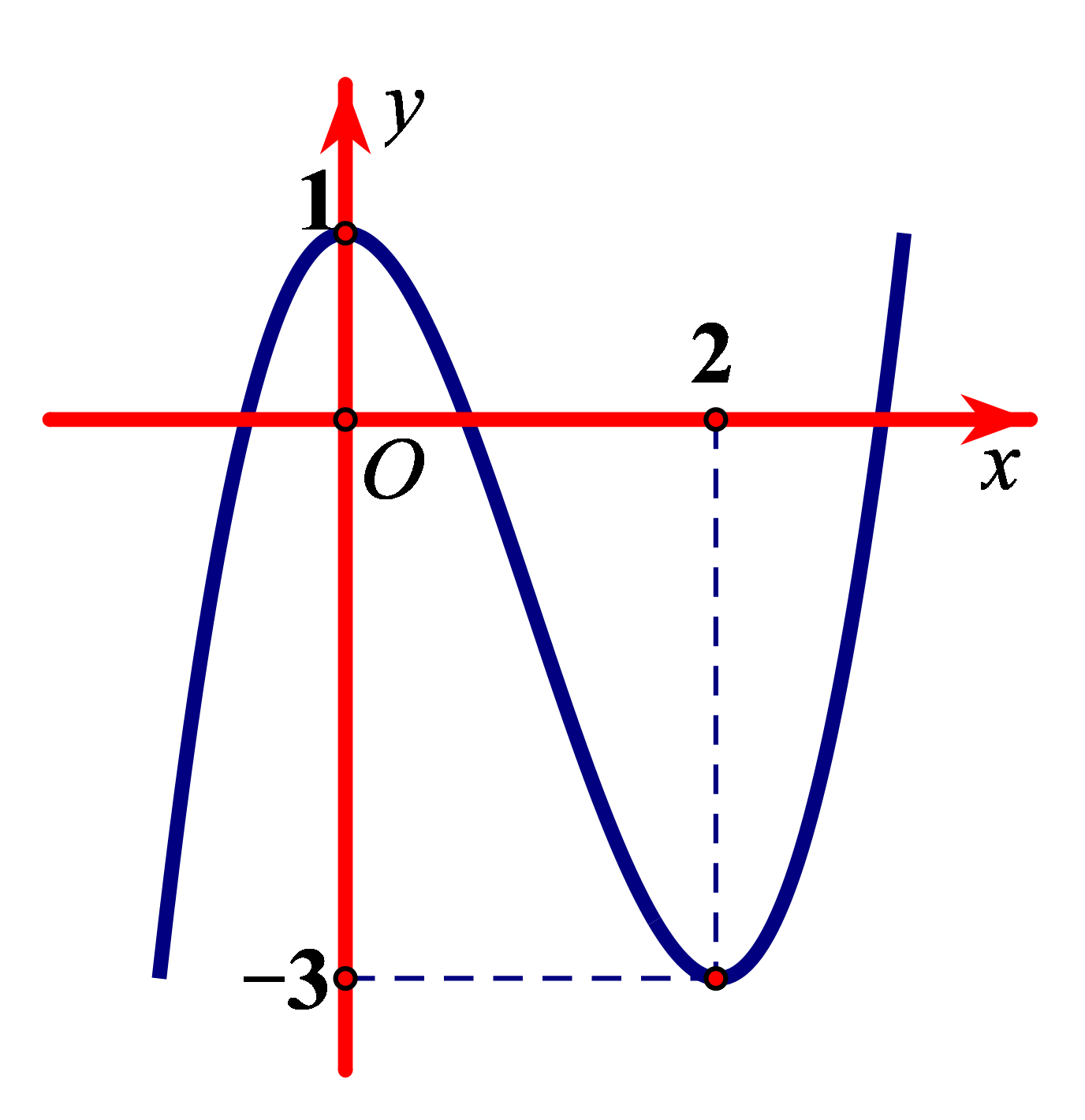
Hàm số đạt cực đại tại điểm nào dưới đây?

A. $x = - 3$. B. $x = 1$. C. $x = 0$. D. $x = 2$.

Hướng dẫn giải

Chọn C

• Đồ thị đang đi lên sau đó đổi hướng đi xuống tại điểm $x = 0$ nên hàm số đạt cực đại tại điểm $x = 0$

Ví dụ 2. Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ $\mathbb{R}$, có đồ thị như hình vẽ.

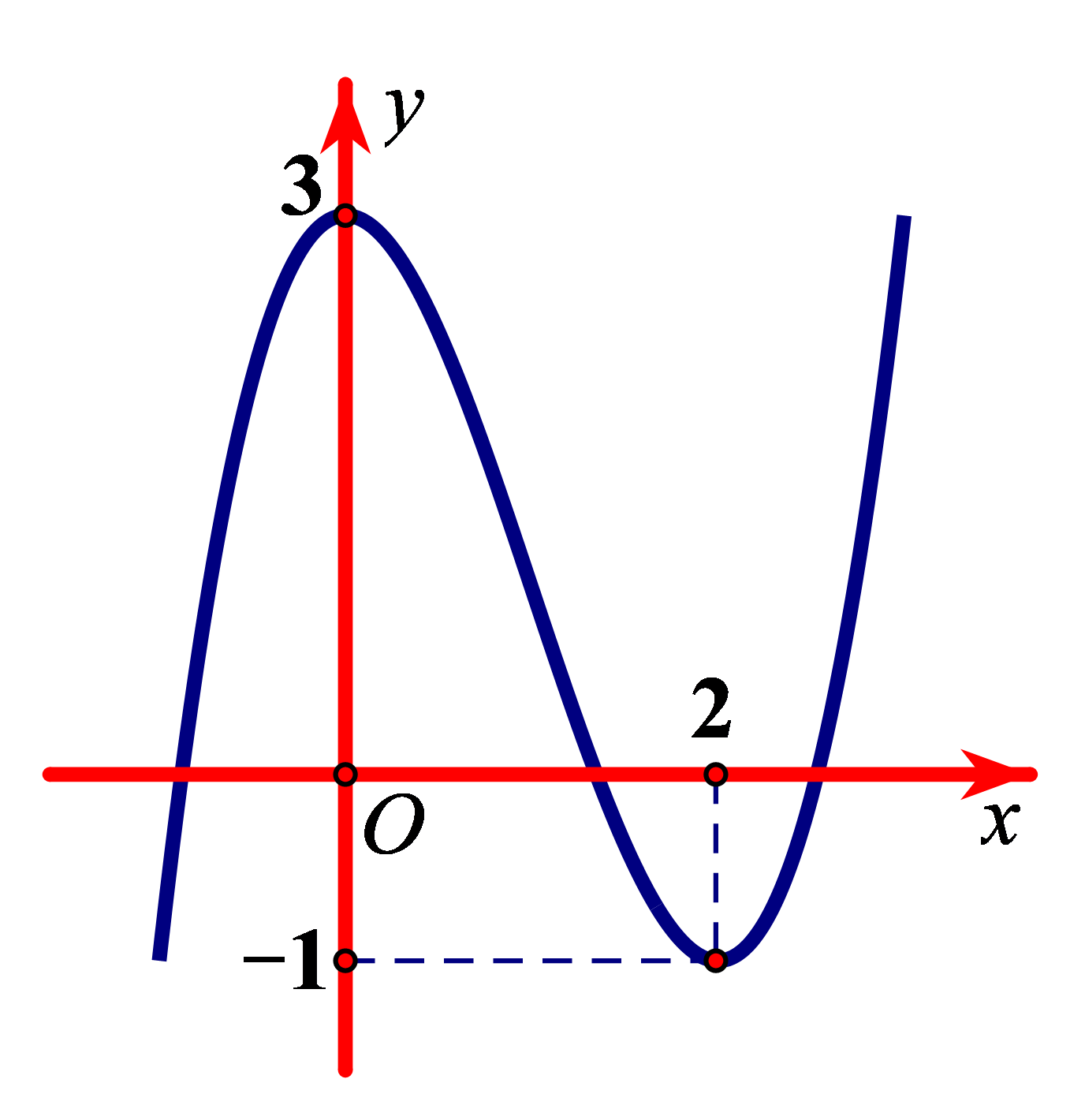
Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực tiểu tại $x = 3$. B. Giá trị cực đại của hàm số bằng $0$.

C. Giá trị cực tiểu của hàm số bằng $- 1$. D. Hàm số đạt cực tiểu tại $x = - 1$.

Hướng dẫn giải

Chọn C

• Đồ thị đang đi lên sau đó đổi hướng đi xuống tại điểm $x = 0$ nên hàm số đạt cực đại tại điểm $x = 0$ và giá trị cực đại bằng $f(0) = 3$.

• Đồ thị đang đi xuống sau đó đổi hướng đi lên tại điểm $x = 2$ nên hàm số đạt cực tiểu tại điểm $x = 2$ và giá trị cực tiểu bằng $f(2) = - 1$.

Vậy đáp án C đúng.

Ví dụ 3. Cho hàm số $y = f(x)$ xác định, liên tục trên đoạn $\lbrack - 1;\ \ 3\rbrack$ $\lbrack - 1;\ \ 3\rbrack$ và có đồ thị như hình vẽ.

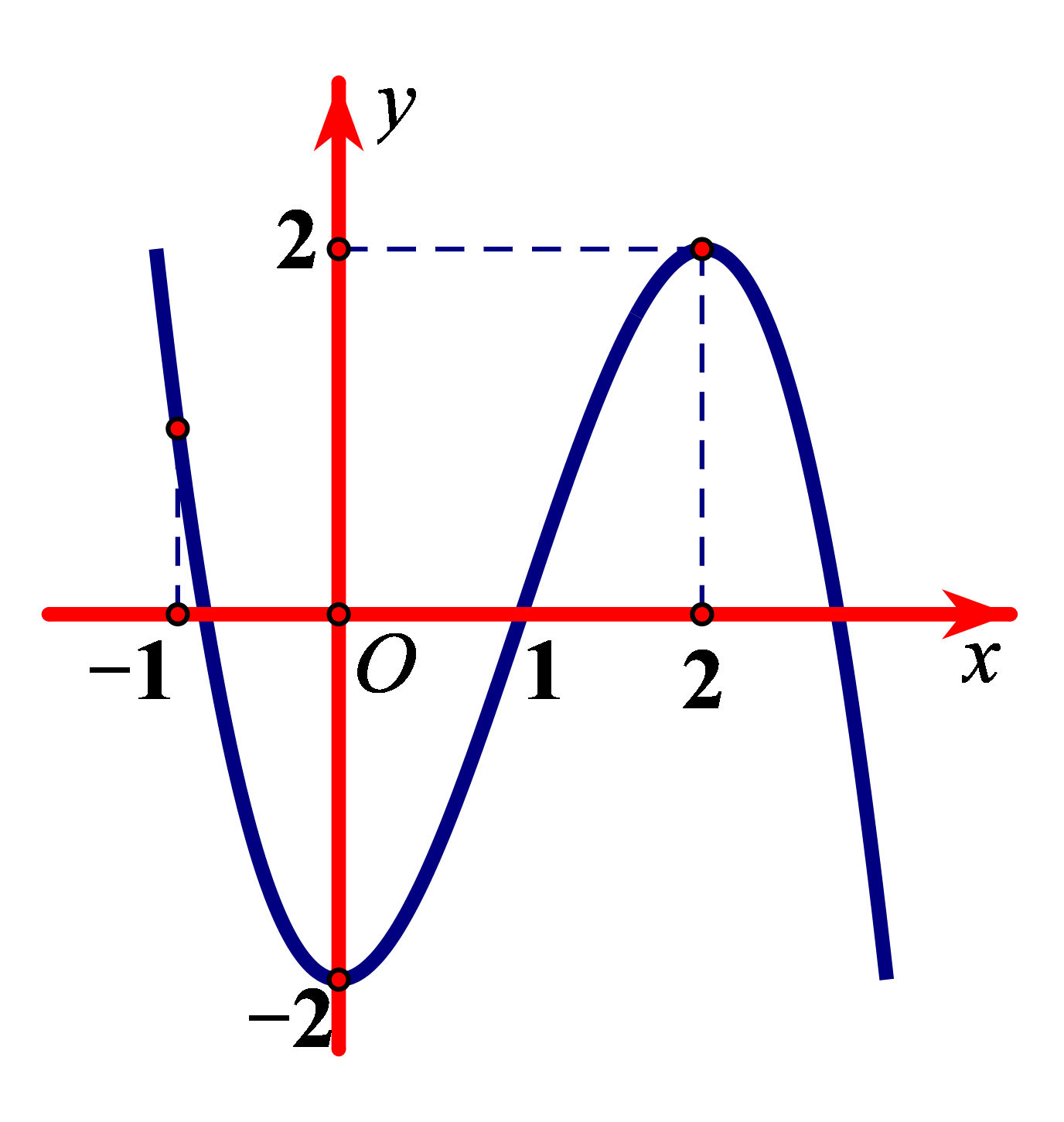
Khẳng định nào sau đây đúng?

A. Hàm số đạt cực đại tại $x = - 1$ và $x = 2$.

B. Hàm số đạt cực tiểu tại $x = 0$, $x = 3$.

C. Hàm số đạt cực tiểu tại $x = 0$, cực đại tại $x = 2$.

D. Hàm số đạt cực tiểu tại $x = 0$, cực đại tại $x = - 1$.

Hướng dẫn giải

Chọn C

• Đồ thị đang đi xuống sau đó đổi hướng đi lên tại điểm $x = 0$ nên hàm số đạt cực tiểu tại điểm $x = 0$

• Đồ thị đang đi lên sau đó đổi hướng đi xuống tại điểm $x = 2$ nên hàm số đạt cực đại tại điểm $x = 2$

Vậy đáp án C đúng.

Ví dụ 4. Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ $\mathbb{R}$, có đồ thị như hình vẽ.

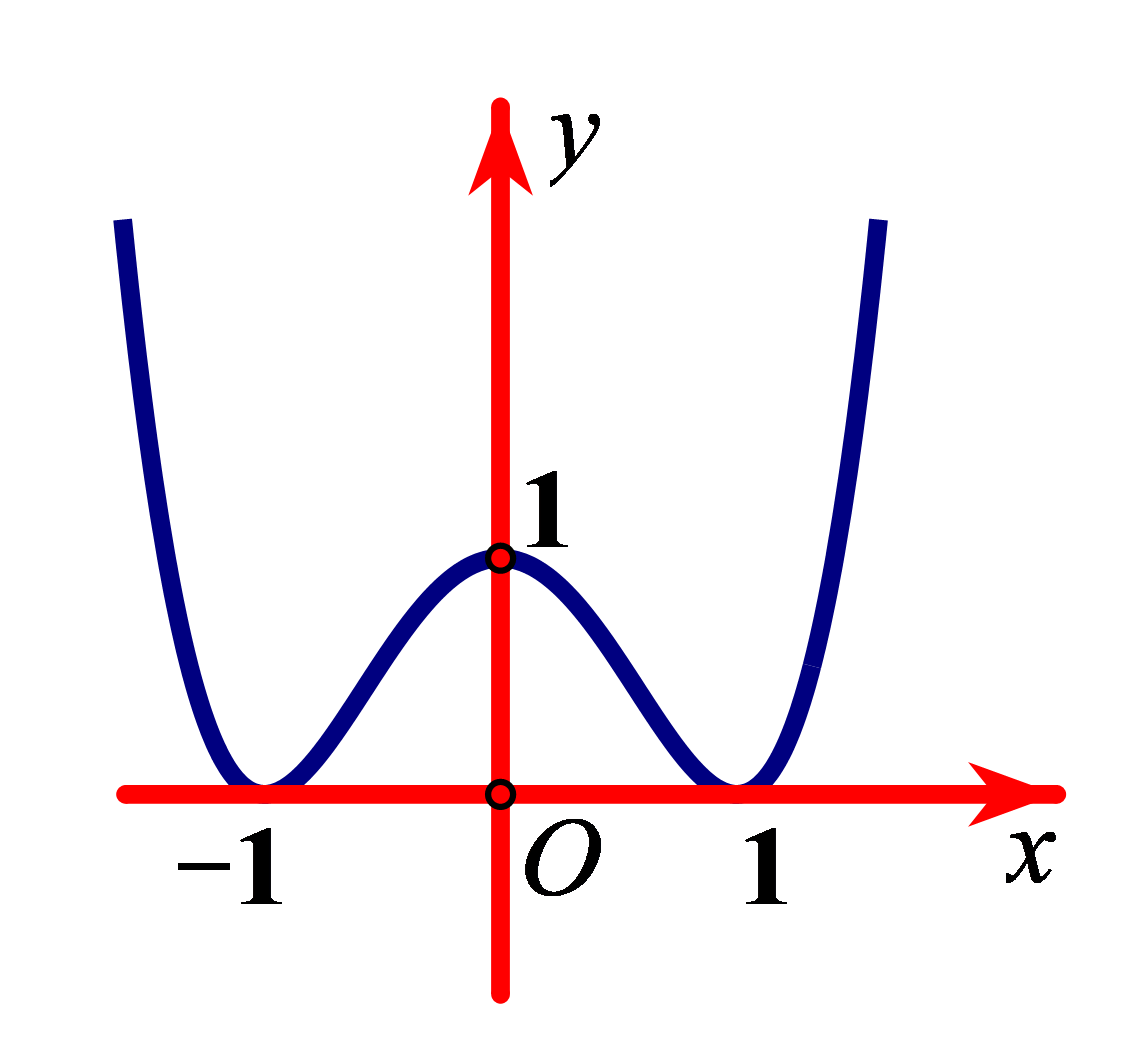
Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực tiểu tại $x = 0$.

B. Hàm số đạt cực đại tại $x = 1$.

C. Hàm số đạt cực đại tại $x = - 1$ và tại $x = 1$.

D. Hàm số đạt cực tiểu tại $x = - 1$ và tại $x = 1$.

Hướng dẫn giải

Chọn D

• Đồ thị đang đi xuống sau đó đổi hướng đi lên tại điểm $x = - 1$ và tại điểm $x = 1$ nên hàm số đạt cực tiểu tại điểm $x = - 1$ và điểm $x = 1$.

• Đồ thị đang đi lên sau đó đổi hướng đi xuống tại điểm $x = 0$ nên hàm số đạt cực đại tại điểm $x = 0$.

Vậy đáp án D đúng.

Ví dụ 5. Đường cong bên là đồ thị của hàm số $y = ax^{4} + bx^{2} + c$ $y = ax^{4} + bx^{2} + c$ với $a,b,c$ là số thực và $a \neq 0$ $a \neq 0$.

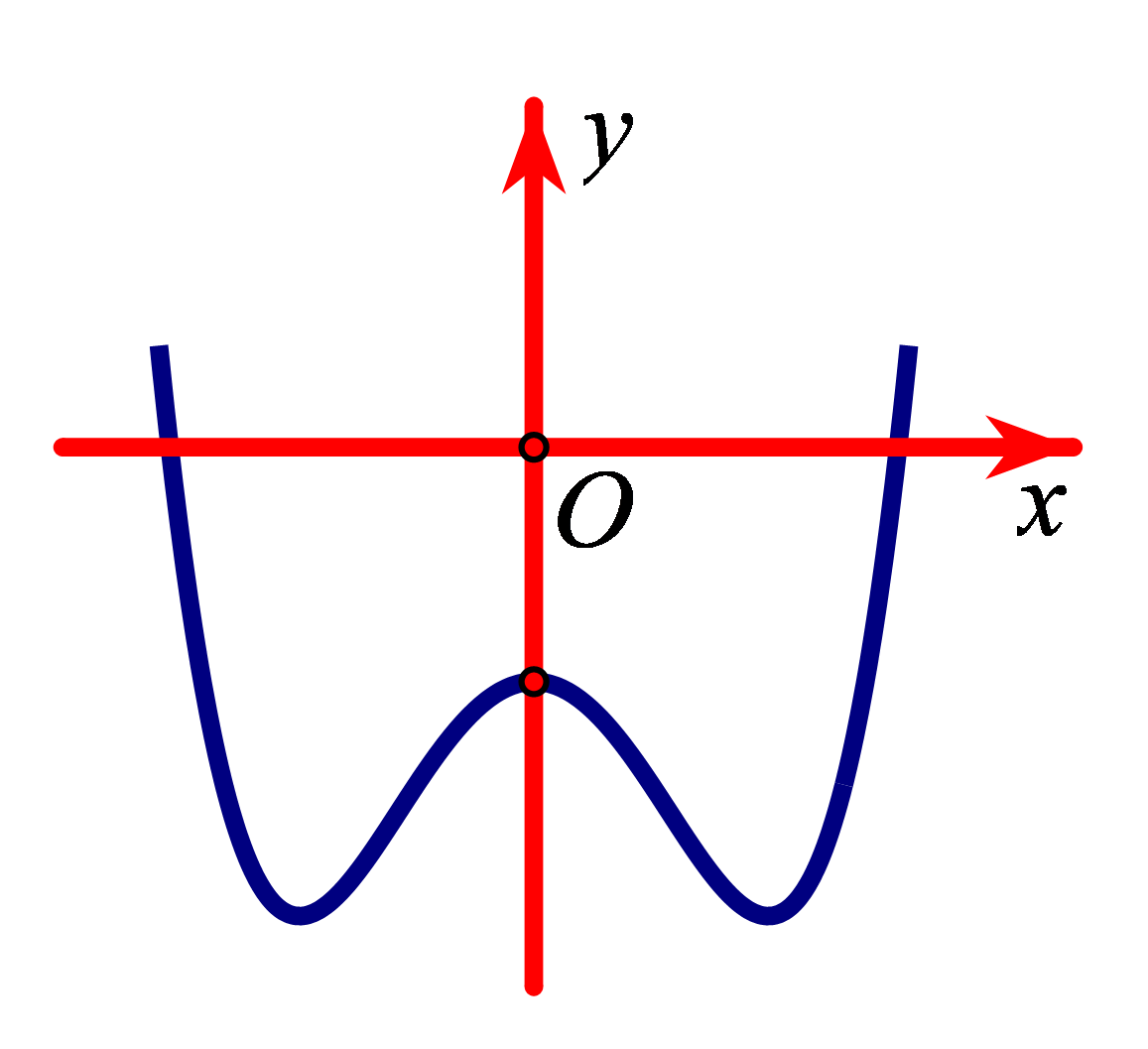
Mệnh đề nào dưới đây đúng?

A. Phương trình $y = 0$ có ba nghiệm thực phân biệt.

B. Phương trình $y = 0$ có đúng một nghiệm thực.

C. Phương trình $y = 0$ có hai nghiệm thực phân biệt.

D. Phương trình $y = 0$ có vô số nghiệm thực.

Hướng dẫn giải

Chọn C

Phương trình $y = 0$ là phương trình hoành độ giao điểm của đồ thị hàm số $y = f(x)$ và trục hoành $Ox$ $(y = 0)$. Số nghiệm của phương trình tương ứng số giao điểm giữa chúng (kiến thức lớp 9)

Ta thấy đồ thị của hàm số có hai giao điểm (phân biệt) với trục hoành $Ox$, nên phương trình $y = 0$ có hai nghiệm phân biệt

Vậy đáp án C đúng.

C. Bài tập vận dụng tự rèn luyện có hướng dẫn chi tiết

Bài tập 1. Cho hàm số $y = f(x)$ xác định, liên tục trên các khoảng $( - \infty;\ \ 0)$ $( - \infty;\ \ 0)$ và $(0;\ \ + \infty)$ $(0;\ \ + \infty)$, có đồ thị là đường cong như hình vẽ.

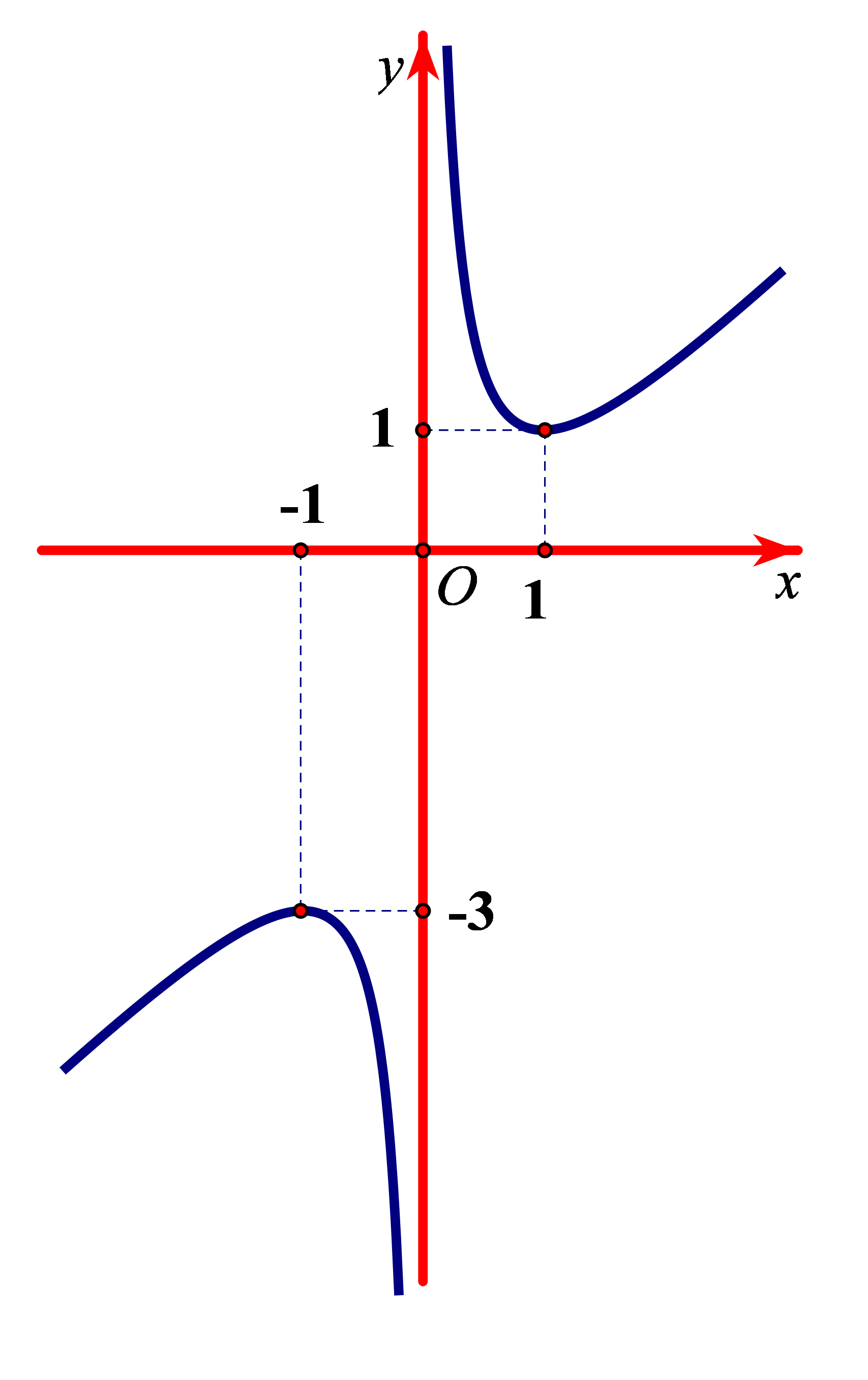
Hàm số đạt cực tiểu tại điểm nào dưới đây?

A. $x = 0$. B. $x = - 3$. C. $x = - 1$. D. $x = 1$.

Bài tập 2. Cho hàm số $y = f(x)$ xác định, liên tục trên các khoảng $( - \infty;\ \ 0)$ $( - \infty;\ \ 0)$ và $(0;\ \ + \infty)$ $(0;\ \ + \infty)$, có đồ thị là đường cong như hình vẽ.

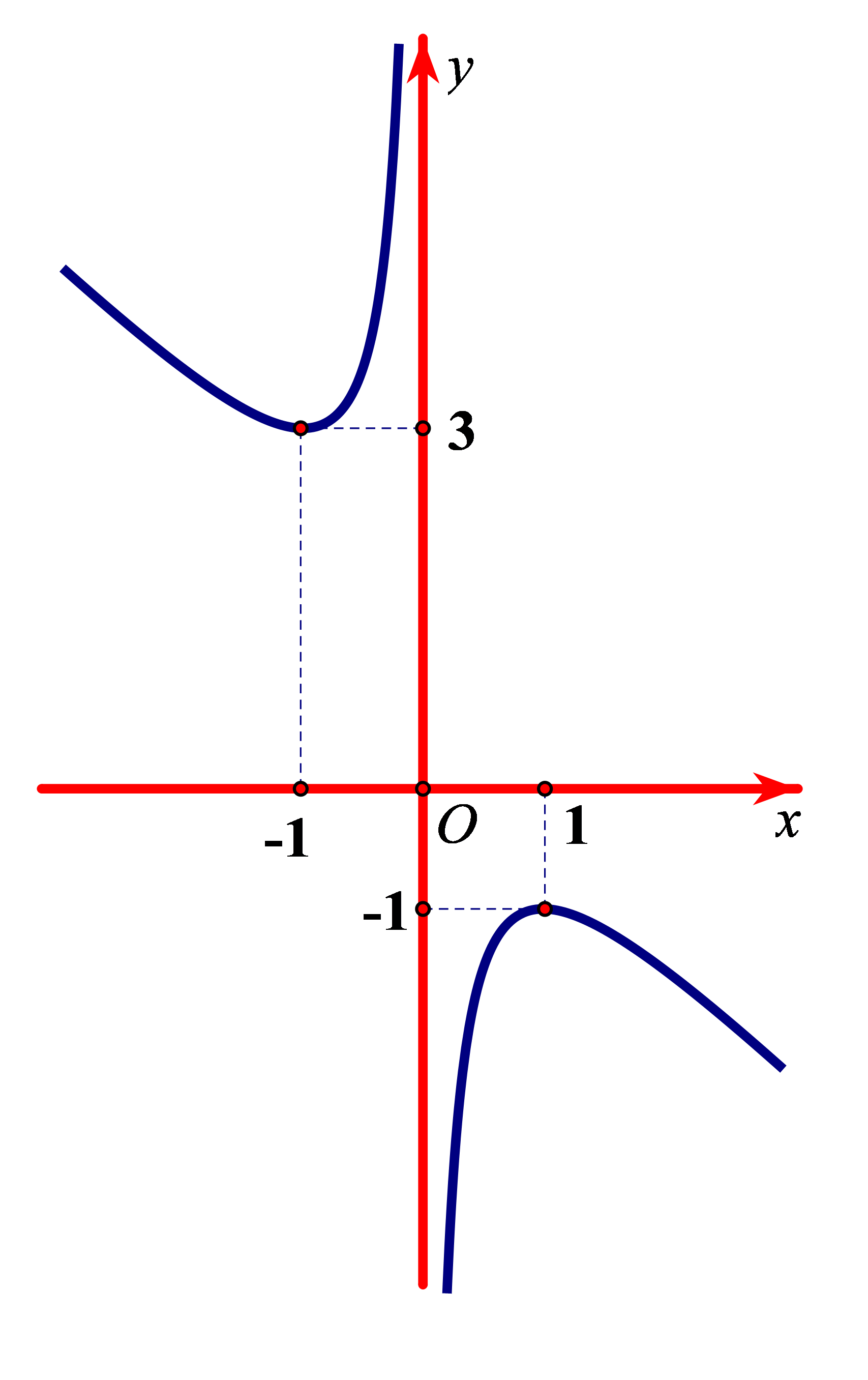
Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực tiểu tại $x = 3$. B. Giá trị cực đại của hàm số bằng $0$.

C. Giá trị cực tiểu của hàm số bằng 3. D. Hàm số đạt cực tiểu tại $x = 1$.

Bài tập 3. Cho hàm số $y = f(x)$ xác định, liên tục trên đoạn $\lbrack - \pi;\ \ \pi\rbrack$ $\lbrack - \pi;\ \ \pi\rbrack$ và có đồ thị như hình vẽ.

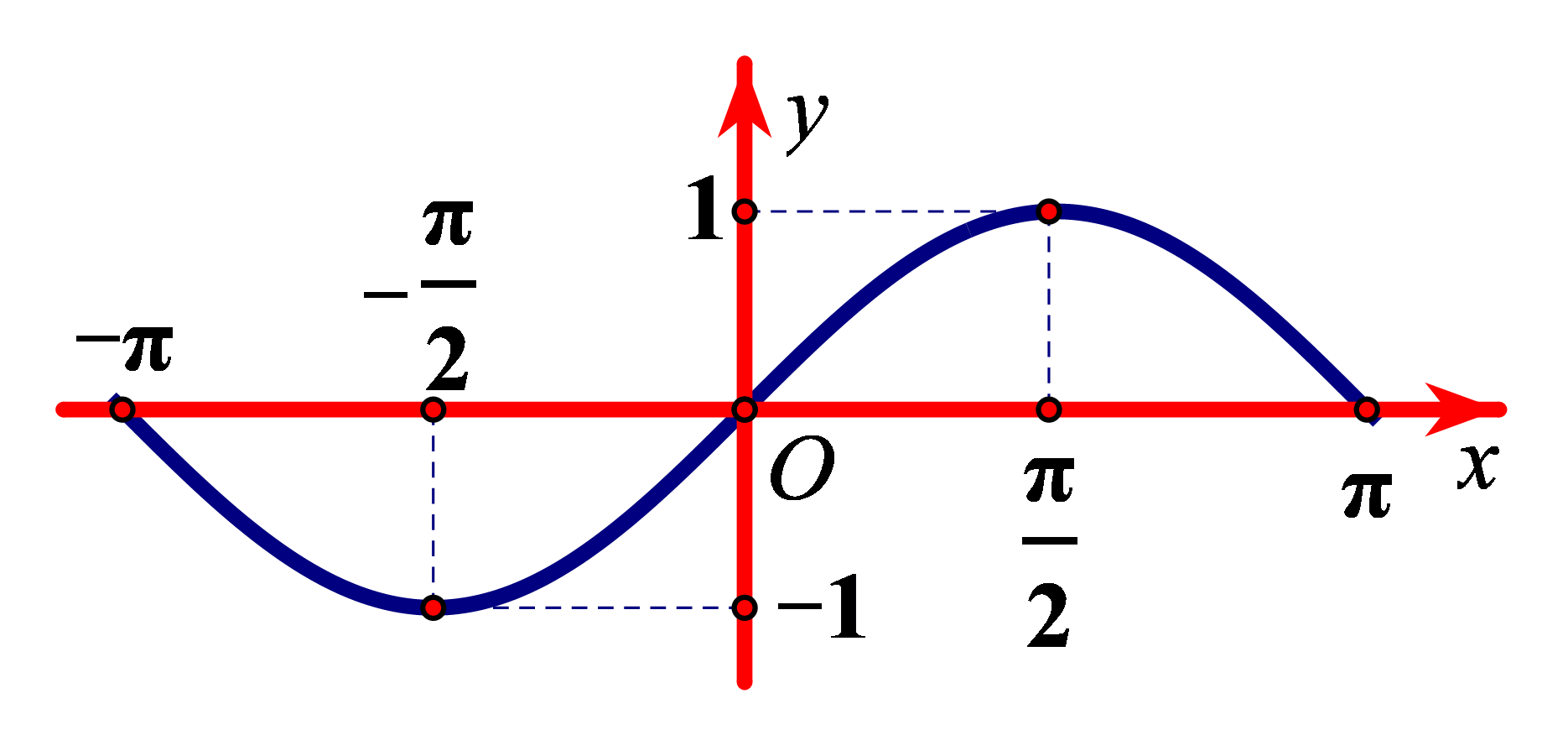
Khẳng định nào sau đây đúng?

A. Hàm số đạt cực đại tại $x = - \pi$ $x = - \pi$ và $x = \pi$ $x = \pi$.

B. Hàm số đạt cực tiểu tại $x = - \frac{\pi}{2}$ $x = - \frac{\pi}{2}$, cực đại tại $x = \frac{\pi}{2}$ $x = \frac{\pi}{2}$.

C. Hàm số đạt cực tiểu tại $x = - 1$, cực đại tại $x = 1$.

D. Hàm số đạt cực tiểu tại $x = 0$, cực đại tại $x = 1$.

Bài tập 3. Cho hàm số $y = f(x)$ xác định, liên tục trên đoạn $\lbrack - \pi;\ \ \pi\rbrack$ $\lbrack - \pi;\ \ \pi\rbrack$ và có đồ thị như hình vẽ.

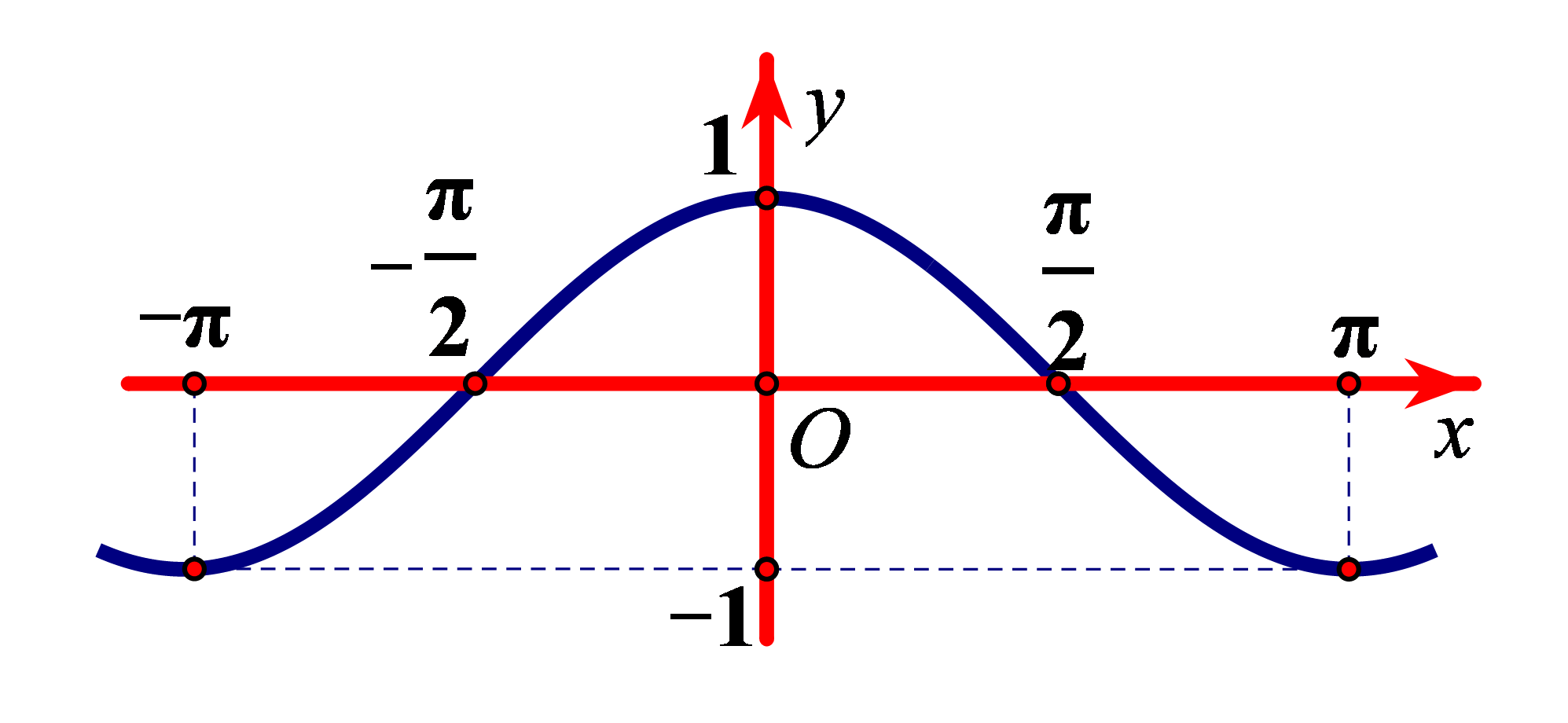
Khẳng định nào sau đây đúng?

A. Hàm số đạt cực đại tại $x = - \pi$ $x = - \pi$ và $x = \pi$ $x = \pi$.

B. Hàm số đạt cực tiểu tại $x = - \pi$ $x = - \pi$ và $x = \pi$ $x = \pi$.

C. Hàm số đạt cực tiểu tại $x = - 1$, cực đại tại $x = 1$.

D. Hàm số đạt cực tiểu tại $x = - \frac{\pi}{2}$ $x = - \frac{\pi}{2}$, cực đại tại $x = \frac{\pi}{2}$ $x = \frac{\pi}{2}$.

Bài tập 4. Cho đồ thị hàm số $y = f(x)$ (với $m$ là tham số) như hình vẽ.

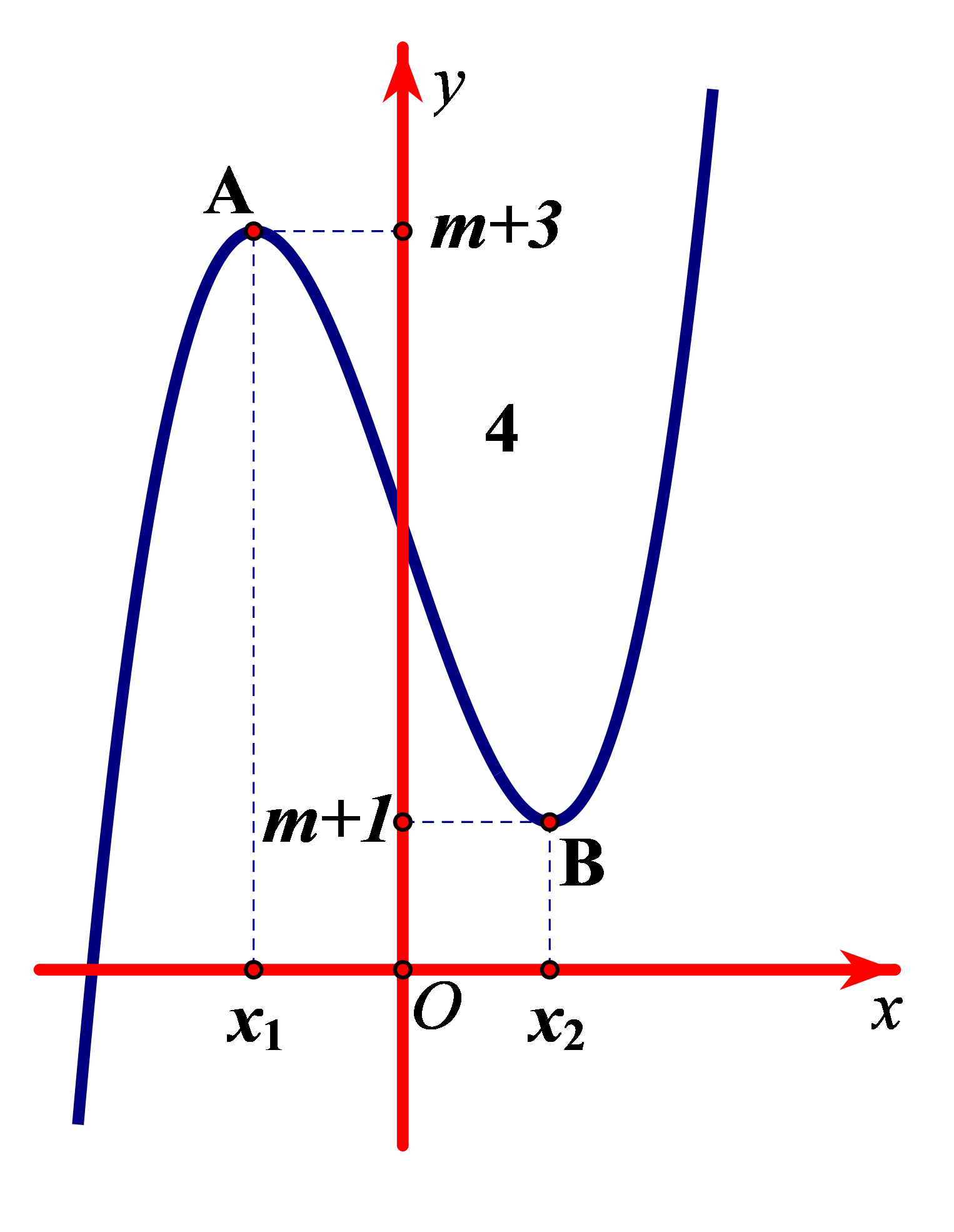
Đồ thị luôn có có toạ độ điểm cực đại là $A\left( x_{1};\ \ m + 3 \right)$ $A\left( x_{1};\ \ m + 3 \right)$, toạ độ điểm cực tiểu là $B\left( x_{2};\ \ m + 1 \right)$ $B\left( x_{2};\ \ m + 1 \right)$. Giá trị của tham số $m$ để phương trình $f(x) = 0$ có ba nghiệm phân biệt là

A. Không có $m$ nào. B. $m < - 3\ \ hay\ \ m > - 1$ $m < - 3\ \ hay\ \ m > - 1$.

C. $m = - 2$. D. $- 3 < m < - 1$.

Bài tập 5. Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ $\mathbb{R}$ và có đồ thị là đường cong như hình vẽ.

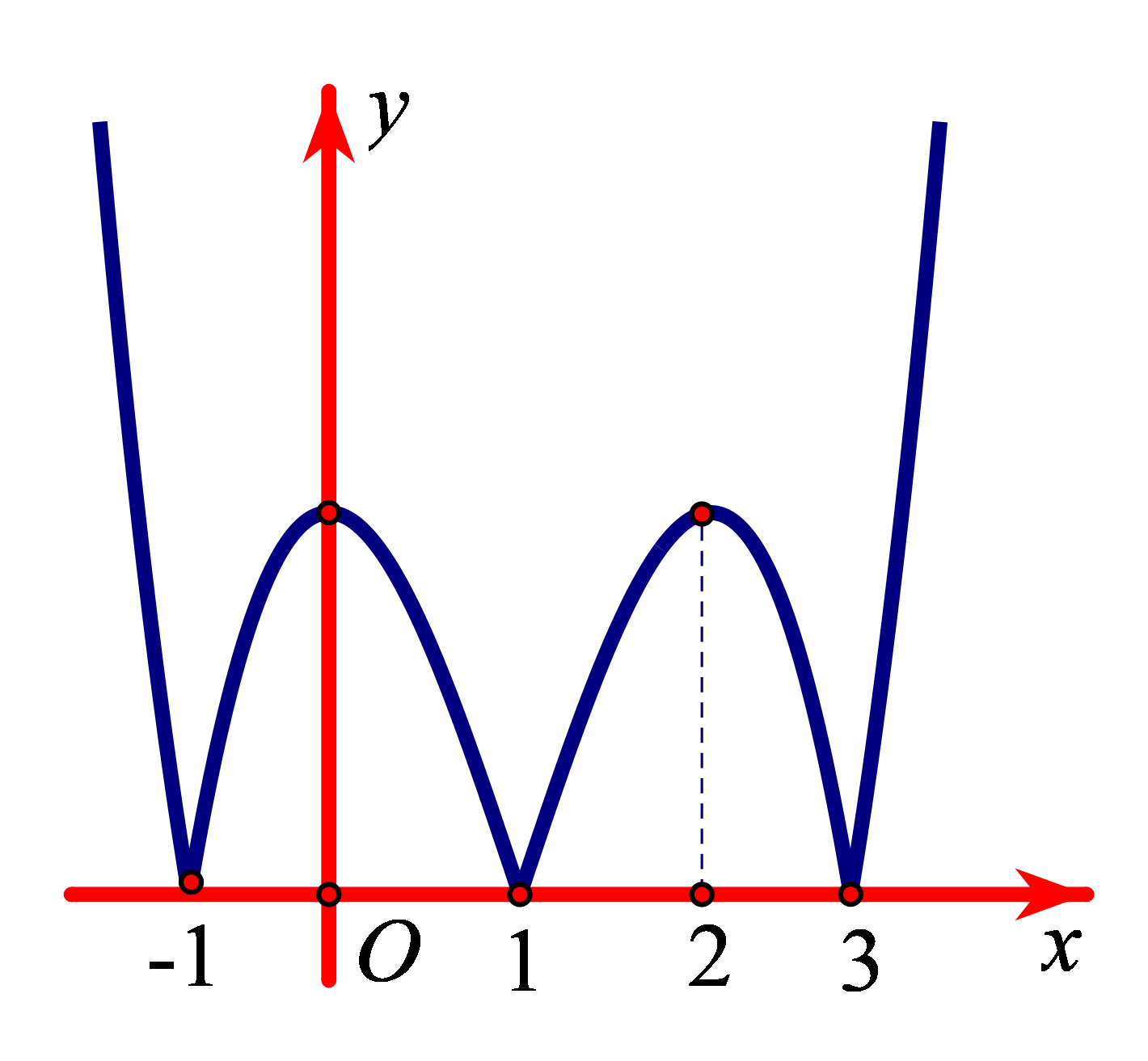
Hàm số đạt cực tiểu tại điểm nào dưới đây?

A. $x = - 1;x = 1;x = 3$. B. $x = 0;x = 2$.

C. $x = - 1;x = 0;x = 1;x = 2;x = 3$. D. Không có điểm nào.

Bài tập 6. Cho hàm số $y = f(x)$ xác định, liên tục trên đoạn $\lbrack - 2;\ \ 3\rbrack$ $\lbrack - 2;\ \ 3\rbrack$ và có đồ thị như hình vẽ.

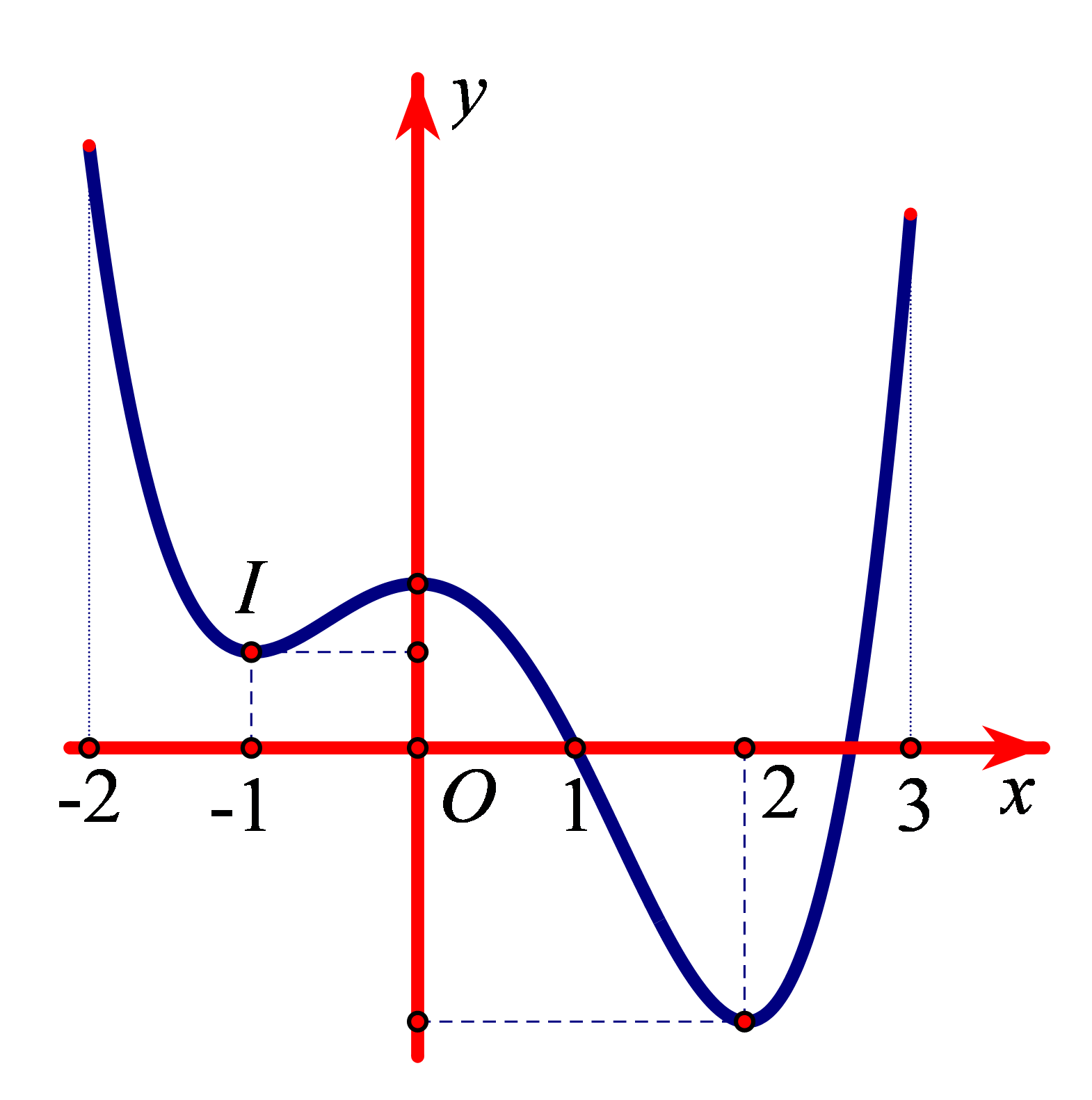
Khẳng định nào sau đây đúng?

A. Hàm số đạt cực đại tại $x = - 2$ và $x = 3$.

B. Hàm số đạt cực tiểu tại $x = 2$, $x = 1$.

C. Hàm số đạt cực tiểu tại $x = - 1;x = 2$, cực đại tại $x = 0$.

D. Hàm số đạt cực tiểu tại $x = - 2;x = - 1$, cực đại tại $x = 2;x = 3$.

Bài tập 7. Cho hàm số $y = f(x)$ xác định, liên tục trên đoạn $\lbrack - 2;\ \ 3\rbrack$ $\lbrack - 2;\ \ 3\rbrack$ và có đồ thị như hình vẽ.

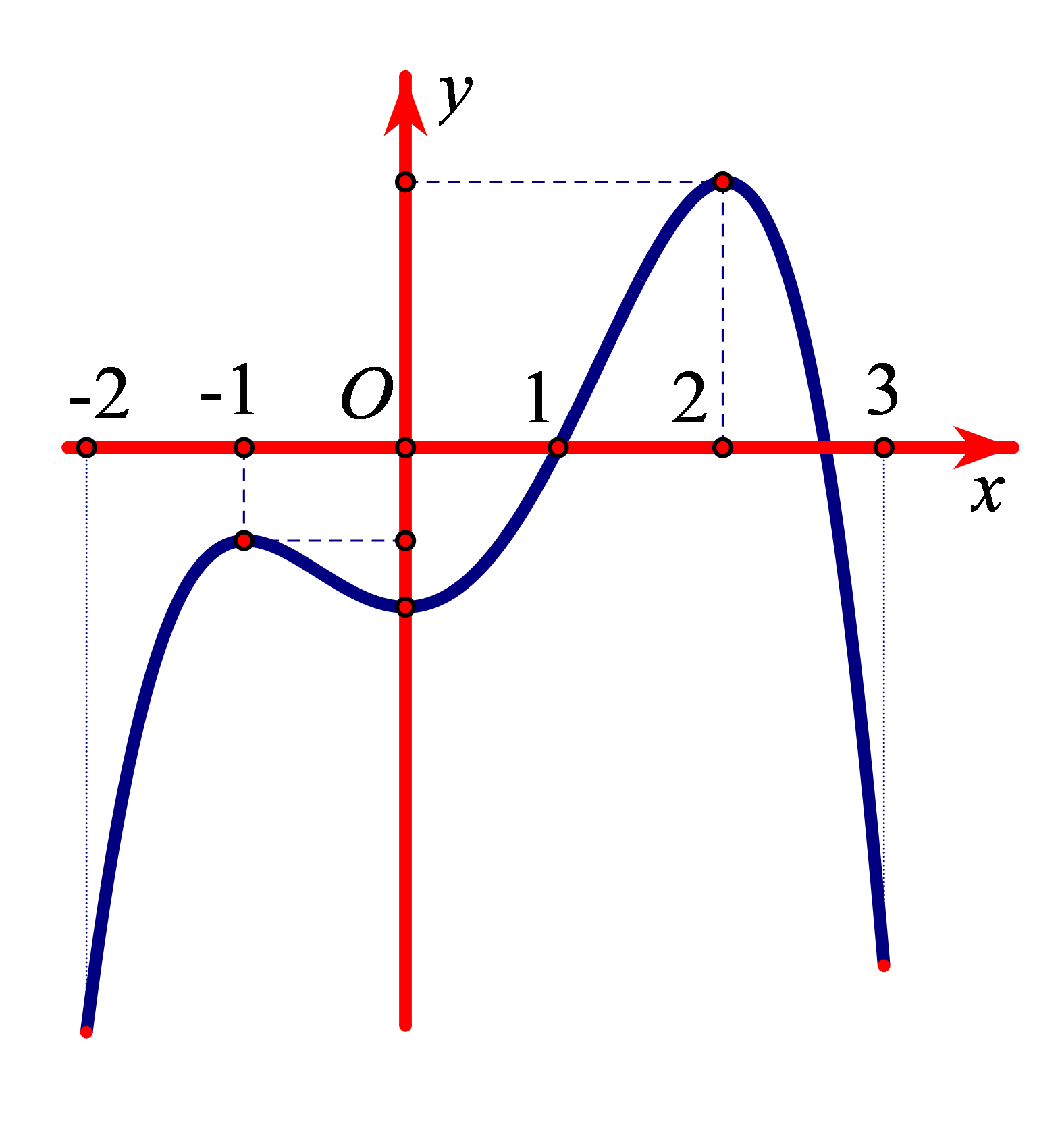
Khẳng định nào sau đây đúng?

A. Hàm số đạt cực tiểu tại $x = - 2$ và $x = 3$.

B. Hàm số đạt cực đại tại $x = 2$, $x = 1$.

C. Hàm số đạt cực đại tại $x = - 1;x = 2$, cực tiểu tại $x = 0$.

D. Hàm số đạt cực đại tại $x = - 2;x = - 1$, cực tiểu tại $x = 2;x = 3$.

Bài tập 8. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên.

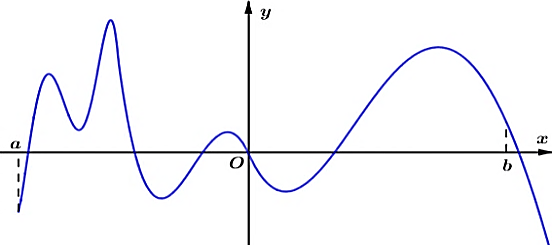
Hàm số có bao nhiêu điểm cực tiểu trên khoảng $(a;b)$?

A. 4. B. 2. C. 7. D. 3.

📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.

---------------------------------------------------

Việc nắm vững cách xác định cực trị của hàm số khi biết đồ thị giúp học sinh tiết kiệm thời gian, hạn chế sai sót và nâng cao hiệu quả làm bài thi. Thông qua chuyên đề này, người học không chỉ củng cố kiến thức về cực trị hàm số mà còn rèn luyện kỹ năng phân tích đồ thị – nền tảng quan trọng để chinh phục các câu hỏi vận dụng trong kỳ thi THPT Quốc gia môn Toán.

Xem thử Tải về

Chọn file muốn tải về: