Bài tập xác định cực trị của hàm số trị tuyệt đối dựa vào đồ thị hàm số
Cách tìm cực trị của hàm số trị tuyệt đối - có đáp án
Trong quá trình ôn thi THPT Quốc gia môn Toán, các bài tập xác định cực trị của hàm số trị tuyệt đối dựa vào đồ thị thường gây khó khăn cho học sinh do sự xuất hiện của điểm gấp khúc và tính không trơn của đồ thị. Việc đọc đúng đồ thị giúp thí sinh nhanh chóng nhận biết cực đại, cực tiểu của hàm số trị tuyệt đối mà không cần xử lý đạo hàm phức tạp. Bài viết này tập trung hệ thống hóa dạng bài thường gặp, hỗ trợ người học tiếp cận hiệu quả và chính xác.
A. Bài tập minh họa tìm cực trị của hàm trị tuyệt đối dựa vào đồ thị hàm số
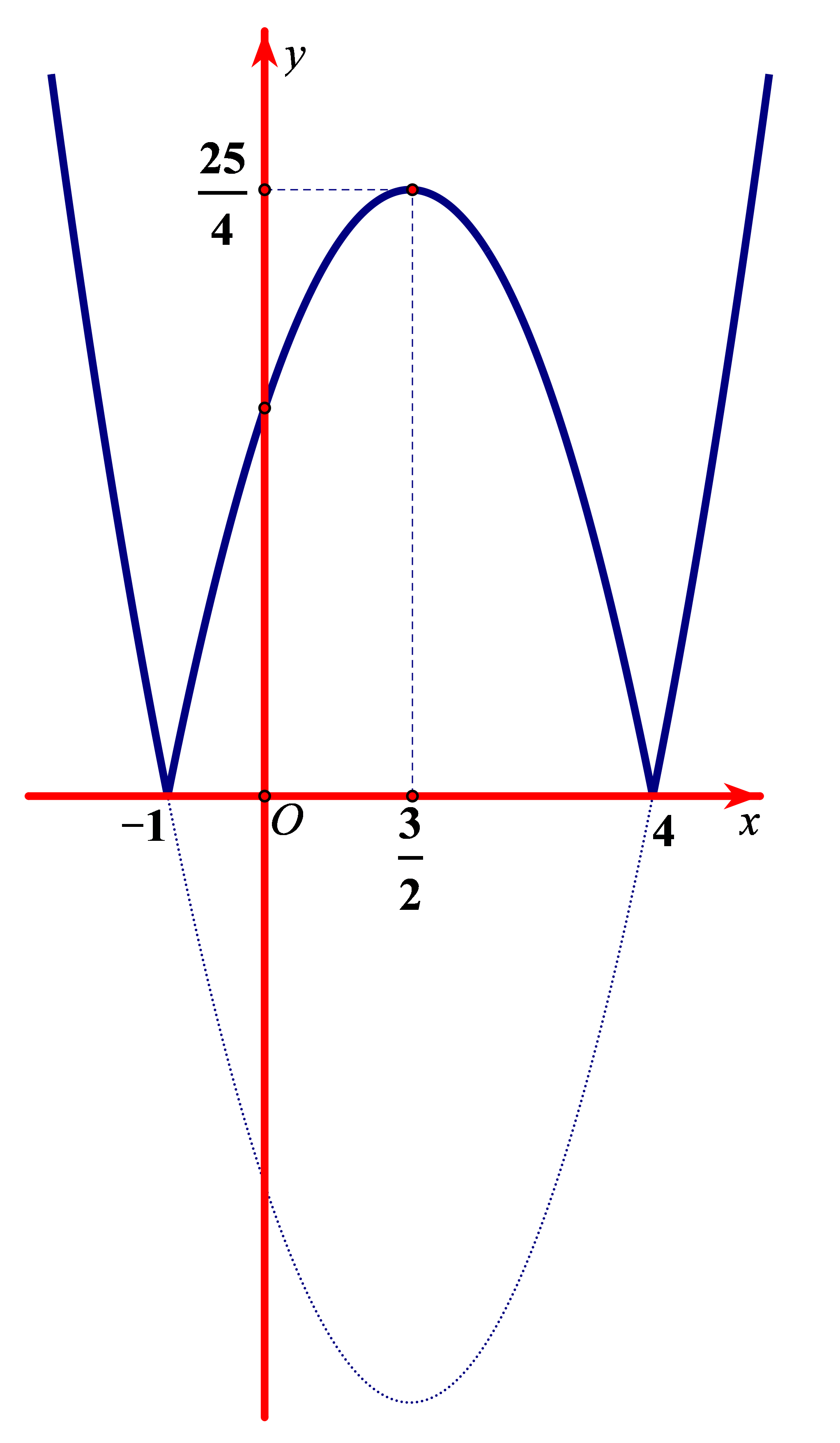
Ví dụ 1. Đường cong bên (nét đậm) là đồ thị của hàm số 
\(y = f(x) = \left| x^{2} - 3x - 4 \right|\). Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại \(x =
\frac{25}{4}\). B. Hàm số đạt cực tiểu tại \(x = 0\).
C. Giá trị cực đại bằng \(\frac{3}{2}\). D. Giá trị cực tiểu bằng 0.
Hướng dẫn giải
Chọn D
• Đồ thị đang đi xuống sau đó đổi hướng đi lên tại điểm \(x = - 1\) và tại điểm \(x = 4\) nên hàm số đạt cực tiểu tại điểm \(x = - 1\) và điểm \(x = 4\). Giá trị cực tiểu \(f( - 1) = f(4) = \mathbf{0}\).
• Đồ thị đang đi lên sau đó đổi hướng đi xuống tại điểm \(x = \frac{3}{2}\) nên hàm số đạt cực đại tại điểm \(x = \frac{3}{2}\). Giá trị cực đại bằng \(f\left( \frac{3}{2}
\right) = \frac{25}{4}\).
Vậy đáp án D đúng.
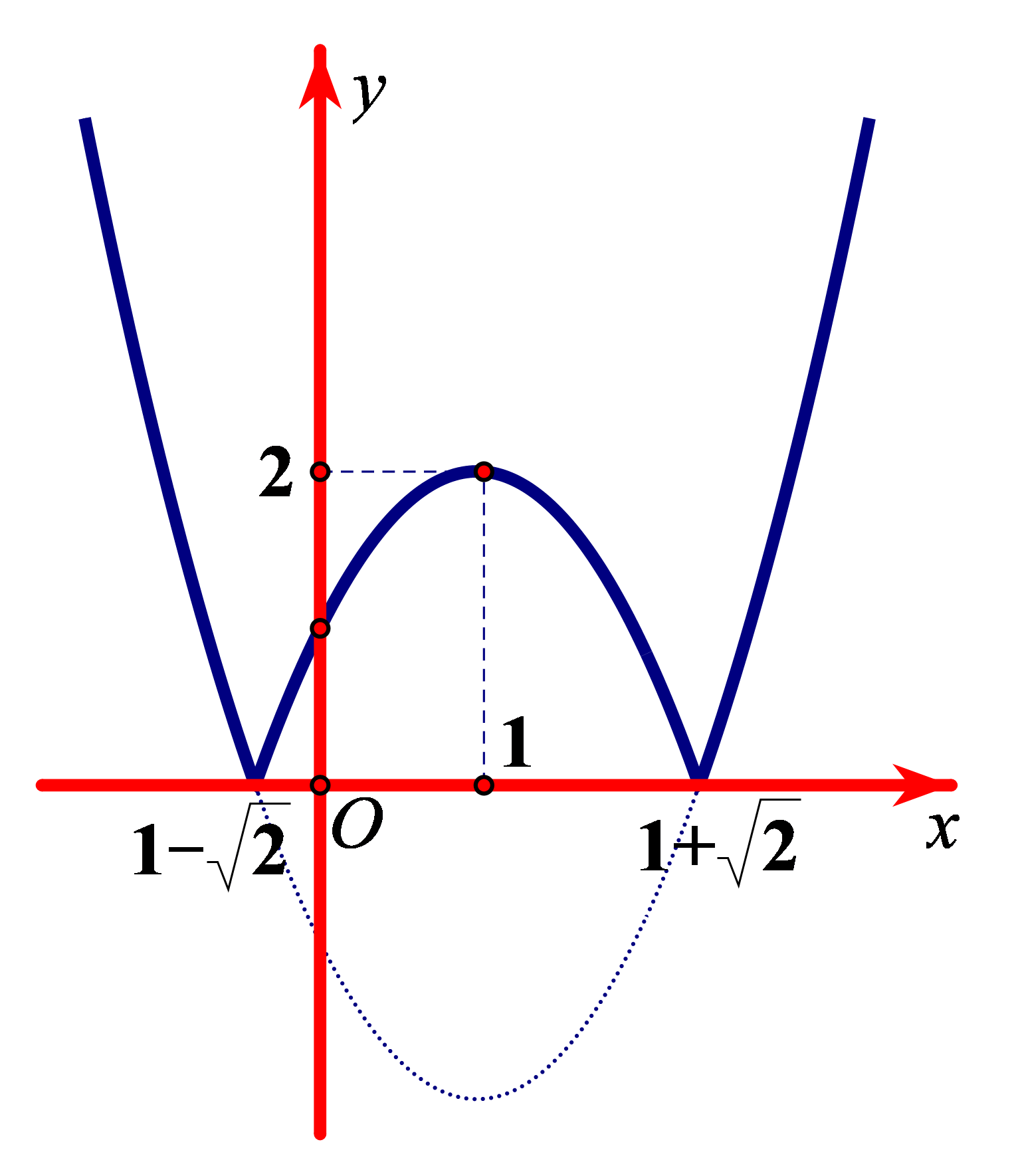
Ví dụ 2. Đường cong bên (nét đậm) là đồ thị của hàm số \(y = f(x) = \left| x^{2} - 2x - 1 \right|\). Xét các phát biểu sau đây có bao nhiêu phát biểu đúng?
(1): Hàm số có một điểm cực đại và hai điểm cực tiểu
(2): Giá trị cực đại bằng \(f(1) = 2\) và giá trị cực tiểu \(f\left( 1 - \sqrt{2}
\right) = f\left( 1 + \sqrt{2} \right) = 0\).
(3): Hàm số chỉ có một điểm cực đại và không có điểm cực tiểu
(4): Hàm số đạt cực đại tại \(x = 1\) và đạt cực tiểu tại \(x = 1 + \sqrt{2} >
0\), loại điểm \(x = 1 - \sqrt{2} <
0\).
A. 1 phát biểu đúng. B. 2 phát biểu đúng.
C. 3 phát biểu đúng. D. 4 phát biểu đúng.
Hướng dẫn giải
Chọn B
(1): đúng. Hàm số có một điểm cực đại \(x =
1\) và hai điểm cực tiểu \(x = 1 -
\sqrt{2}\), \(x = 1 +
\sqrt{2}\).
(2): đúng. Hàm số đạt cực đại tại điểm \(x
= 1\), giá trị cực đại bằng \(f(1) =
2\); hàm số đạt cực tiểu tại điểm \(x =
1 - \sqrt{2}\), \(x = 1 +
\sqrt{2}\), giá trị cực tiểu \(f\left(
1 - \sqrt{2} \right) = f\left( 1 + \sqrt{2} \right) = 0\).
(3): sai. Vì hàm số có một điểm cực đại và hai điểm cực tiểu.
(4): sai. Vì tập xác định của hàm số là \(\mathbb{R}\) nên không loại điểm nào.
Vậy có 2 phát biểu đúng.
Ví dụ 3. Đường cong bên (nét đậm) là đồ thị của hàm số \(y = f(x) = \left| x^{4} - 4x^{2} \right|\).
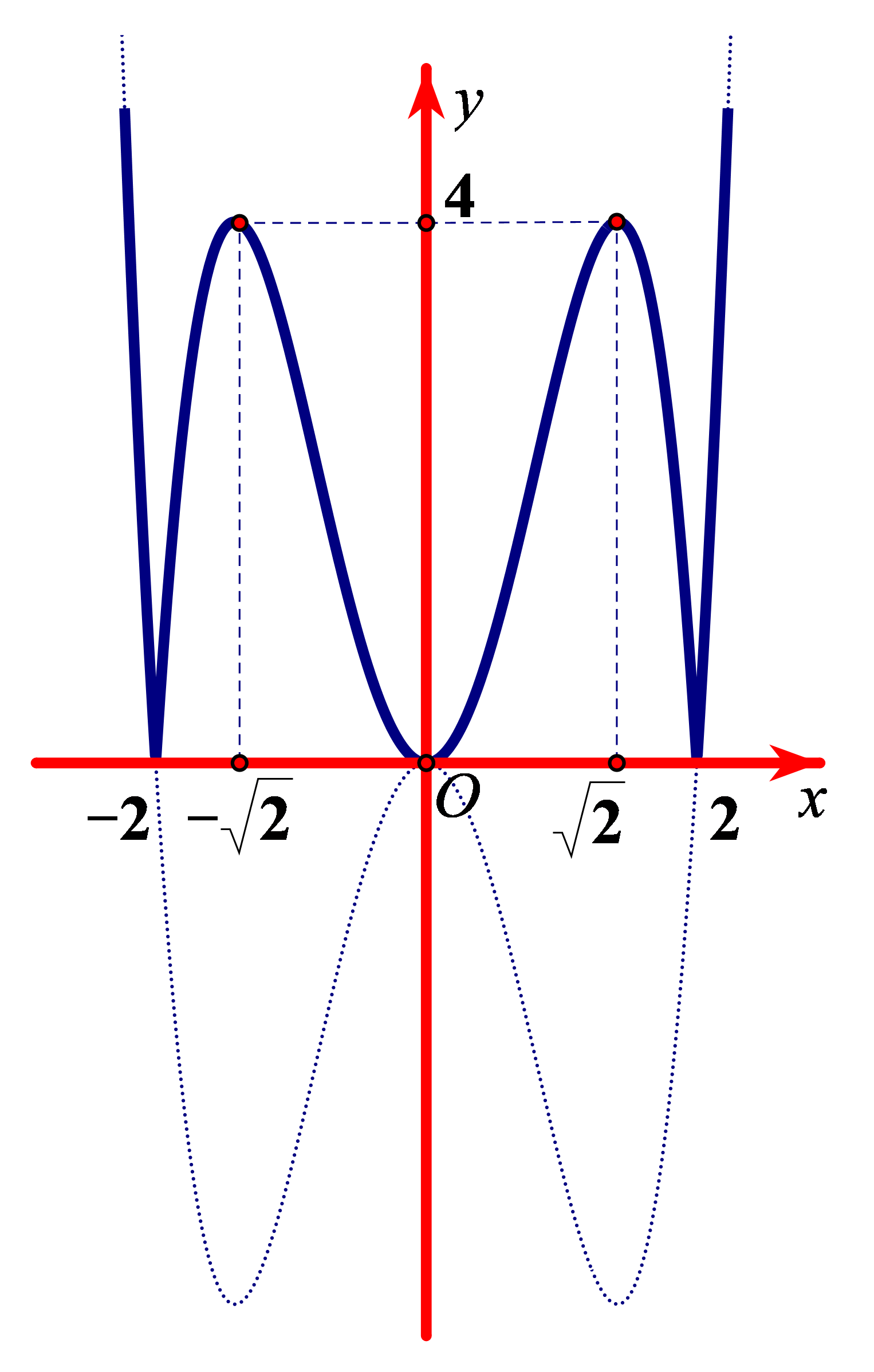
Xét các phát biểu sau đây có bao nhiêu phát biểu đúng?
(1): Hàm số có hai điểm cực đại và ba điểm cực tiểu
(2): Giá trị cực đại bằng \(f\left( - \sqrt{2}
\right) = f\left( \sqrt{2} \right) = 4\) và giá trị cực tiểu \(f( - 2) = f(0) = f(2) = 0\).
(3): Hàm số chỉ có hai điểm cực đại và một điểm cực tiểu
(4): Hàm số đạt cực đại tại \(x = \sqrt{2}
> 0\) và đạt cực tiểu tại \(x =
0\), loại điểm \(x = - 2 <
0\) và \(x = - \sqrt{2}\).
A. 1 phát biểu đúng. B. 2 phát biểu đúng.
C. 3 phát biểu đúng. D. 4 phát biểu đúng.
Hướng dẫn giải
Chọn B
(1): đúng. Hàm số có hai điểm cực đại \(x =
- \sqrt{2},x = \sqrt{2}\) và ba điểm cực tiểu \(x = - 2,x = 0,x = 2\)
(2): đúng. Hàm số đạt cực đại tại điểm \(x
= - \sqrt{2},x = \sqrt{2}\), giá trị cực đại bằng \(f\left( - \sqrt{2} \right) = f\left( \sqrt{2}
\right) = 4\); hàm số đạt cực tiểu tại điểm \(x = - 2,x = 0,x = 2\), giá trị cực tiểu \(f( - 2) = f(0) = f(2) = 0\).
(3): sai. Vì hàm số có hai điểm cực đại và ba điểm cực tiểu.
(4): sai. Vì tập xác định của hàm số là \(\mathbb{R}\) nên không loại điểm nào.
Vậy có 2 phát biểu đúng.
B. Bài tập vận dụng tự rèn luyện có hướng dẫn chi tiết
Bài tập 1. Đường cong bên (nét đậm) là đồ thị của hàm số \(y = f(x) = x^{2} - 2|x| - 1\). Mệnh đề nào dưới đây đúng?
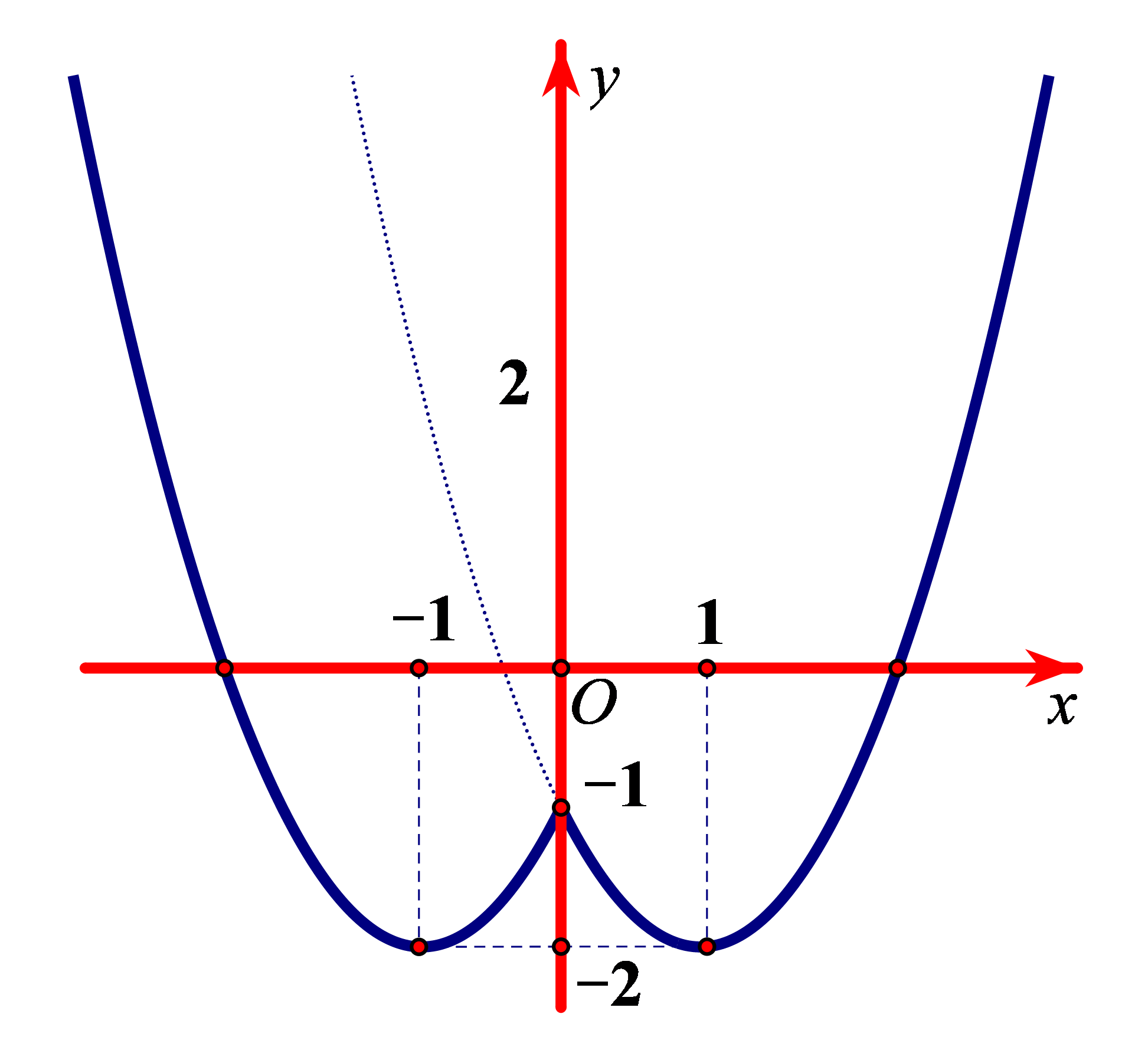
A. Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = - 1,x =
1\).
B. Hàm số chỉ đạt cực tiểu tại \(x = - 1,x
= 1\).
C. Hàm số chỉ đạt cực tiểu tại \(x = -
2\).
D. Hàm số đạt cực đại tại \(x = -
1\) và đạt cực tiểu tại \(x =
1\).
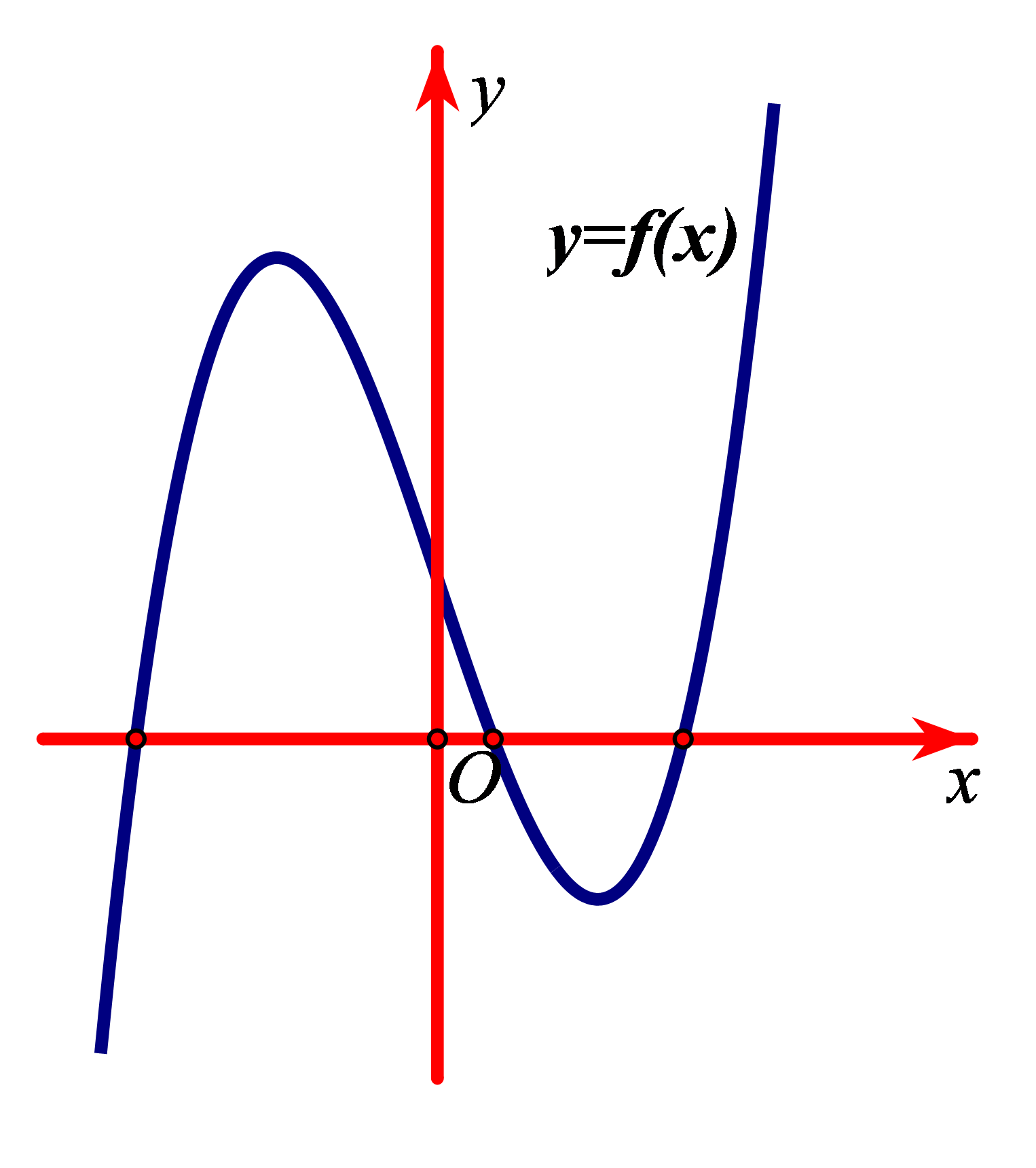
Bài tập 2. Cho đồ thị của hàm số \(y =
f(x)\) như hình vẽ. Suy ra đồ thị của hàm số \(y = \left| f(x) \right|\) có bao nhiêu điểm cực đại, bao nhiêu điểm cực tiểu?
A. 0 điểm cực đại và 0 điểm cực tiểu.
B. 1 điểm cực đại và 0 điểm cực tiểu.
C. 3 điểm cực đại và 2 điểm cực tiểu.
D. 2 điểm cực đại và 3 điểm cực tiểu.
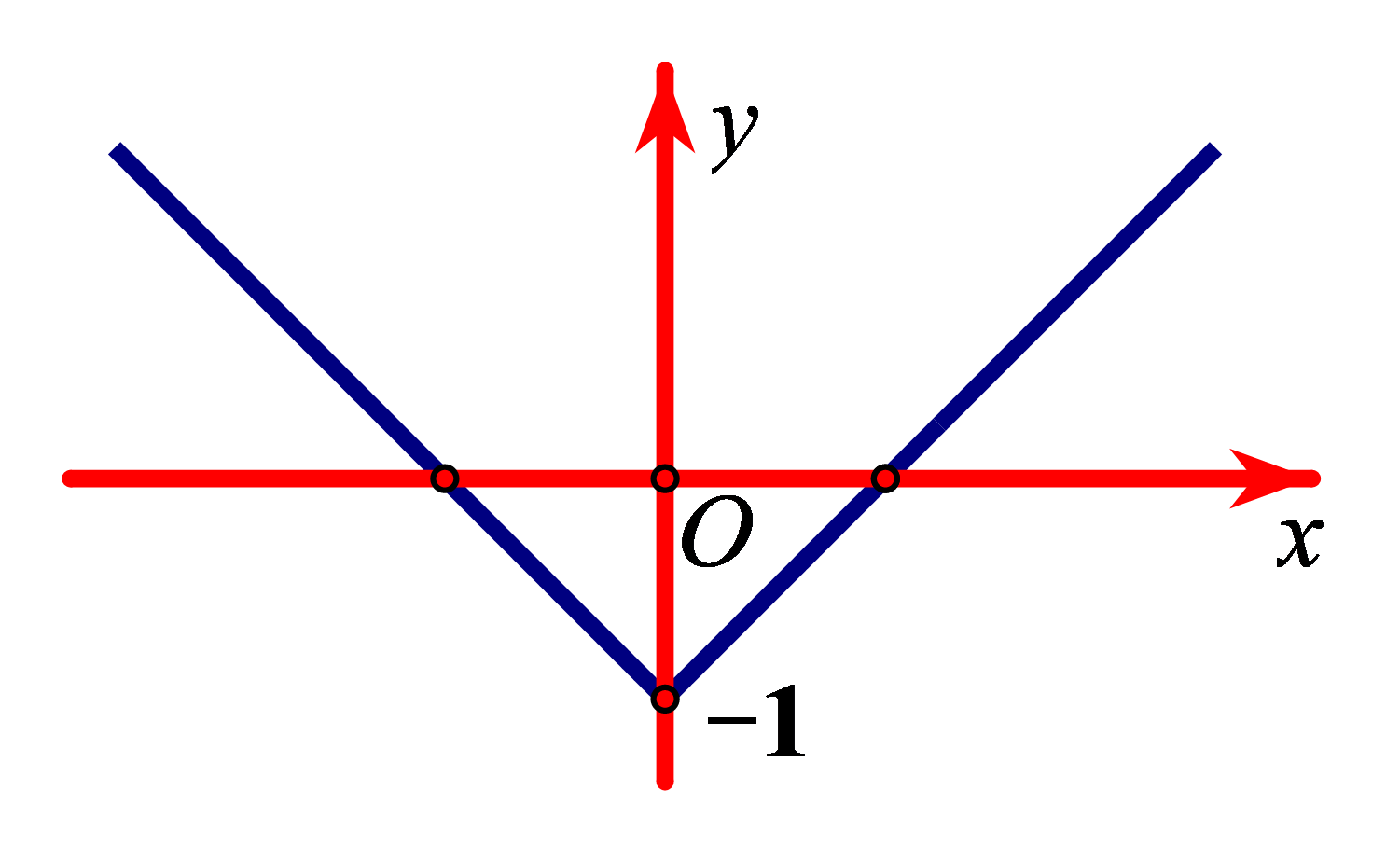
Bài tập 3. Đường bên là đồ thị của hàm số \(y = |x| - 1\). Mệnh đề nào dưới đây đúng?
A. Phương trình \(y = 0\) có hai nghiệm thực phân biệt.
B. Phương trình \(y = 0\) có đúng một nghiệm thực.
C. Phương trình \(y = 0\) có ba nghiệm thực phân biệt.
D. Phương trình \(y = 0\) có vô số nghiệm thực.
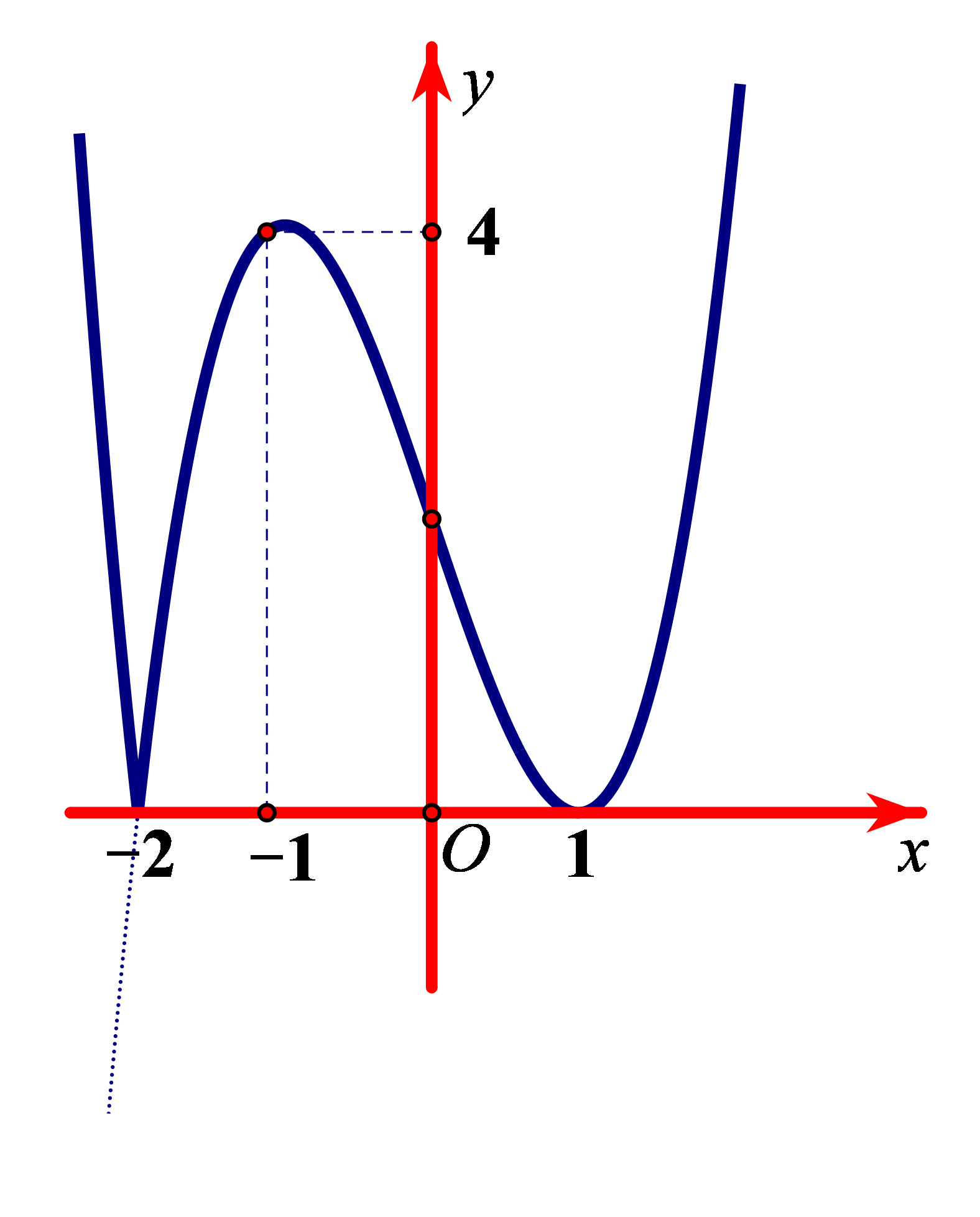
Bài tập 4. Đường cong bên (nét đậm) là đồ thị của hàm số \(y = f(x) = \left| x^{3} - 3x + 2 \right|\). Xét các phát biểu sau đây có bao nhiêu phát biểu đúng?
(1): Hàm số có một điểm cực đại và hai điểm cực tiểu
(2): Giá trị cực đại bằng \(f( - 4) =
2\) và giá trị cực tiểu \(f( - 2) =
f(1) = 0\).
(3): Hàm số chỉ có một điểm cực đại và không có điểm cực tiểu
(4): Hàm số đạt cực tiểu tại \(x = 1 >
0\), loại điểm \(x = - 2 <
0\), \(x = - 1 < 0\).
A. 1 phát biểu đúng. B. 2 phát biểu đúng.
C. 3 phát biểu đúng. D. 4 phát biểu đúng.
✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.
-----------------------------------------------
Việc thành thạo cách xác định cực trị của hàm số trị tuyệt đối dựa vào đồ thị hàm số sẽ giúp học sinh nâng cao tốc độ làm bài và hạn chế sai lầm trong phòng thi. Thông qua hệ thống bài tập này, người học không chỉ củng cố kiến thức về cực trị hàm số trị tuyệt đối mà còn phát triển kỹ năng phân tích đồ thị – yếu tố then chốt để đạt kết quả cao trong kỳ thi THPT Quốc gia môn Toán.
