40 câu hỏi trắc nghiệm Tiệm cận của đồ thị hàm số có đáp án
Tài liệu ôn thi tốt nghiệp THPT quốc gia môn Toán
Mời các bạn tham khảo tài liệu 40 câu hỏi trắc nghiệm tiệm cận của đồ thi hàm số theo từng mức độ. Trong tài liệu sẽ có 4 mức độ khác nhau cho các em tham khảo, ôn tập. Bộ câu hỏi có đáp án đi kèm, chắc chắn là tài liệu tham khảo hữu ích cho các em ôn thi Toán THPT Quốc gia.
Đường tiệm cận là phần nội dung quan trọng được học trong chương trình Toán 12. Tài liệu 40 câu hỏi trắc nghiệm Tiệm cận của đồ thị hàm số có đáp án được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và đề thi THPT Quốc gia. Hi vọng sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán hiệu quả.
1. Đường tiệm cận đứng
Định nghĩa:
Đường thẳng 
\(x = x_{0}\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y =
f(x)\)nếu ít nhất một trong các điều kiện sau đây được thỏa mãn:
\(\lim_{x \rightarrow {x_{0}}^{+}}f(x) = +
\infty\);\(\lim_{x \rightarrow
{x_{0}}^{+}}f(x) = - \infty\);\(\lim_{x
\rightarrow {x_{0}}^{-}}f(x) = + \infty\);\(\lim_{x \rightarrow {x_{0}}^{-}}f(x) = -
\infty\)
2. Đường tiệm cận ngang
Định nghĩa:
Đường thẳng \(y = y_{0}\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y
= f(x)\)nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\lim_{x \rightarrow + \infty}f(x) =
y_{0}\);\(\lim_{x \rightarrow -
\infty}f(x) = y_{0}\)
Chú ý:
- Đồ thị hàm số \(y = \frac{ax + b}{cx +
d},(ad - bc \neq 0,c \neq 0)\) luôn có tiệm cận ngang và tiệm cận đứng lần lượt là \(y = \frac{a}{c}\) \(x = - \frac{d}{c}\).
- Nếu \(y = f(x) =
\frac{P(x)}{Q(x)}\) là hàm số phân thức hữu tỷ.
- Nếu Q(x) = 0 có nghiệm là x0, và x0 không là nghiệm của P(x) = 0 thì đồ thị có tiệm cận đứng là \(x = x_{0}\)
- Nếu bậc (P(x)) ≤ bậc (Q(x)) thì đồ thị có tiệm cận ngang.
3. Bài tập trắc nghiệm có đáp án
Mức độ 1
Câu 1. Phương trình đường tiệm cận đứng của đồ thị hàm số \(y = \frac{2x + 1}{x - 3}\) là:
A. \(x = 2\). B. \(x = - 3\). C. \(x
= 3\). D. \(x = - 2\).
Câu 2. Cho hàm số \(y = f(x)\) có \(\lim_{x \rightarrow + \infty}f(x) =
3\) và \(\lim_{x \rightarrow -
\infty}f(x) = - 3\). Phát biểu nào sau đây đúng?
A. Đồ thị hàm số có 2 đường tiệm cận ngang là \(y = 3\) và \(y =
- 3\).
B. Đồ thị hàm số có 2 đường tiệm cận đứng là \(x = 3\) và \(x =
- 3\).
C. Đồ thị hàm số có duy nhất một đường tiệm cận ngang.
D. Đồ thị hàm số có 2 đường tiệm cận ngang là \(x = 3\) và \(x =
- 3\).
Câu 3. Cho hàm số \(y = f(x)\)có bảng biến thiên như hình vẽ
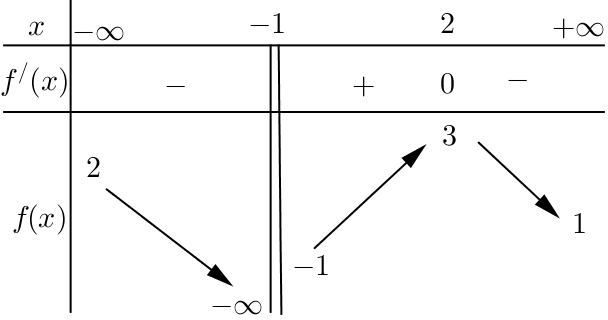
Đường tiệm cận đứng của đồ thị hàm số \(f(x)\) là:
A. \(y = - 1\). B. \(x = - 1\). C. \(x
= 2\). D. \(x = 1\).
Câu 4. Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{2x + 1}{3 - x}\) là:
A. \(y = \frac{2}{3}\). B. \(x = - 2\). C. \(y
= - 2\). D. \(x = 3\).
Câu 5. Phương trình đường tiệm cận đứng của đồ thị hàm số \(y = \frac{3}{x + 2}\) là:
A. \(x = 0\). B. \(x = - 2\). C. \(x
= 3\). D. \(y = 0\).
Câu 6. Cho hàm số \(y = f(x)\) có đồ thị như hình dưới đây.
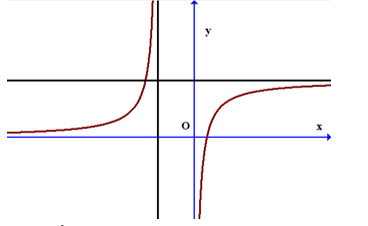
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận?
A. \(4\). B. Không có tiệm cận. C. \(2\). D. 3.
Câu 7. Cho hàm số \(y = f(x)\) có tập xác định là \(\mathbb{R}\backslash\left\{
- 2;1 \right\}\) và \(\underset{x
\rightarrow - 2^{+}}{\lim f(x)} = + \infty\) và \(\underset{x \rightarrow 1^{-}}{\lim f(x)} = +
\infty\). Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng \(x = - 2\) và \(x
= 1\).
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng \(y = 1\) và \(y =
- 1\).
Câu 8. Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{2x + 1}{3 - x}\) là:
A. \(y = \frac{2}{3}\). B. \(x = - 2\). C. \(y
= - 2\). D. \(x = 3\).
Câu 9. Đường thẳng \(y =
\frac{1}{3}\) là tiệm cận ngang của đồ thị hàm số nào dưới đây?
A. \(y = \frac{3x + 1}{x - 3}\) B. \(y = \frac{x + 1}{3x - 3}\) C. \(y = \frac{2x + 1}{3x - 1}\) D. \(y = \frac{- x + 1}{3x - 1}\)
Câu 10. Cho hàm số \(y = f(x)\)có bảng biến thiên như hình vẽ:
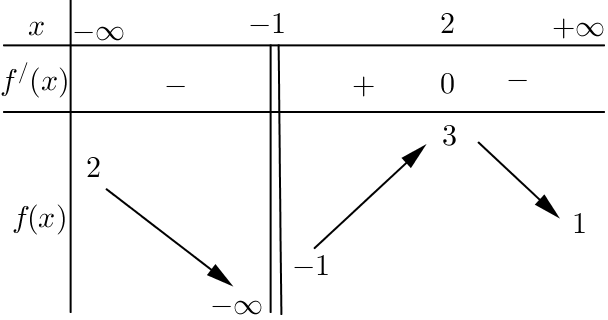
Đồ thị hàm số \(f(x)\) có bao nhiêu tiệm cận ngang?
A. 1. B. 2. C. 3. D. 0.
ĐÁP ÁN MỨC 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
A |
B |
C |
B |
A |
C |
C |
B |
B |
Mức độ 2
Câu 1. Cho hàm số \(f(x) = \frac{1}{\sqrt{4
- x^{2}}}\). Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số không có tiệm cận.
B. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(y = 0\) và hai tiệm cận đứng là các đường thẳng \(x = \pm 2\).
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(y = 0\), không có tiệm cận đứng.
D. Đồ thị hàm số không có tiệm cận ngang, có hai tiệm cận đứng là các đường thẳng \(x = \pm 2\).
Câu 2. Đồ thị hàm số \(y = \frac{x^{2} -
4}{(x + 2)^{2}(x + 3)}\) có bao nhiêu đường tiệm cận?
A. \(1\). B. \(2\). C. \(3\). D. \(4\).
Câu 3. Tổng số các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{x + 2}{\sqrt{x -
3}}\) là:
A. 0. B. 3. C. 1. D. 2.
Câu 4. Các đường tiệm cận của đồ thị hàm số \(y = \frac{2x - 3}{x - 4}\) tạo với hai trục tọa độ một hình chữ nhật có chu vi bằng:
A. \(6\). B. \(12\). C. 8. D. \(16\).
Câu 5. Tìm tất cả các giá trị thực của tham số \(m\) để đường tiệm cận ngang của đồ thị hàm số \(y = \frac{(m + 2)x - 3}{4 - x}\) đi qua điểm \(A( - 1\ ;\ 2)\).
A. \(m = - 2\). B. \(m = 1\). C. \(m =
- 4\). D. \(m = 2\).
Câu 6. Cho hàm số \(y = f(x)\) có bảng biến thiên dưới đây. Hỏi đồ thị hàm số \(y = f(x)\) có bao nhiêu đường tiệm cận?
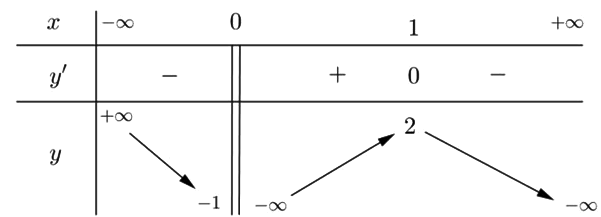
A. 1. B. 2. C. 3. D. 4.
Câu 7. Đồ thị hàm số \(y = \frac{\sqrt{x +
9} - 3}{x^{2} + x}\) có tất cả bao nhiêu đường tiệm cận?
A. 0. B. 3. C. 1. D. 2.
Câu 8. Đồ thị hàm số \(y = \frac{x +
2}{x^{2} - 4x - 12}\) có bao nhiêu đường tiệm cận đứng?
A. 1. B. 2. C. 4. D. 3.
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
---------------------------------------------------------------
Với bộ 40 câu hỏi trắc nghiệm Tiệm cận của đồ thị hàm số có đáp án vừa được chia sẻ, hy vọng bạn đã có thêm tài liệu luyện tập hiệu quả để củng cố kiến thức và nâng cao kỹ năng làm bài trắc nghiệm Toán 12. Dạng toán về tiệm cận không chỉ xuất hiện thường xuyên trong đề thi THPT Quốc gia mà còn giúp học sinh làm chủ kiến thức về sự biến thiên và hình dạng đồ thị hàm số – một chuyên đề nền tảng của giải tích lớp 12.
Để đạt kết quả cao trong kỳ thi, bạn nên thường xuyên luyện tập thêm các dạng câu hỏi tương tự, kết hợp ôn lại lý thuyết, công thức quan trọng và rèn kỹ năng sử dụng máy tính cầm tay. Đừng quên theo dõi chuyên mục “Ôn thi THPT Quốc gia môn Toán” tại [Tên website của bạn] để cập nhật thêm nhiều đề luyện thi, mẹo giải nhanh, và tài liệu trắc nghiệm có đáp án chi tiết. Chúc bạn học tốt, luyện thi hiệu quả và tự tin chinh phục điểm 9, 10 trong kỳ thi sắp tới!
